Lagrange-Methode

Technik zur Lösung von Optimierungsproblemen, in denen die Restriktionen als implizite Funktionen mit der Zielfunktion in der Lagrange-Funktion zusammengefaßt werden. Liegt beispielsweise ein Maximierungsproblem mit der Zielfunktion
(1)                    y  =  f(x1,x2) und der Nebenbedingung in Form einer Gleichung
(2)                    g(x1,x2)  =  0 vor, so lautet die Lagrange-Funktion
(3)                   L(x1,x2,l) = f(x1,x2) + l(g(x1,x2)). Maximiert wird L hinsichtlich x1, x2 und l, so daß die optimalen Werte von x1* und x2* sowohl y maximieren als auch die Restriktion erfüllen. Die Variable


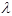
 wird als Lagrange-Multiplikator bezeichnet.