Bernoulli-Prinzip

Entscheidungsprinzip (Entscheidungstheorie) für Risikosituationen. Die möglichen Zielgrößenwerte (mögliche Ereignisse) und deren Eintrittswahrscheinlichkeiten werden explizit berücksichtigt. Das eigentliche (komplexe) Entscheidungsproblem wird in einfachere (hypothetische) Teilprobleme zerlegt, bei denen jeweils nur drei der möglichen Ergebnisse gegeneinander abzuwägen sind. Eine Entscheidung nach dem B. wird in zwei Schritten getroffen: Zuerst wird auf der Grundlage einfacher Entscheidungsprobleme eine Nutzenfunktion U bestimmt, die den Ergebnissen eas reelle Nutzenwerte U (eas) zuordnet. Dann wird diejenige Alternative gewählt, deren Ergebnissen der höchste Nutzenerwartungswert entspricht. Nach dem B. ist der Präferenzwert der Alternative Aa (a = 1, 2, ..., n) definiert als         


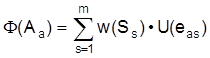
  die Zielfunktion lautet:         


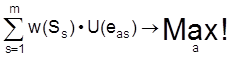
                                                                                                                                                                                          Dabei bezeichnet eas den Wert des Ergebnisses bei Wahl der Alternative Aa und Eintreten des Umweltzustandes Ss (s = 1, 2, ..., m) und w (Ss) die Eintrittswahrscheinlichkeit des Umweltzustandes Ss. Zur Ermittlung des Nutzenwertes U (eas) eines Ergebnisses eas            


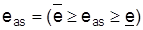
wird dem Entscheider hypothetisch die Wahl geboten zwischen dem sicheren Ergebnis eas und einer Lotterie, bei der das Ergebnis 


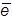
 mit Wahrscheinlichkeit w und das Ergebnis


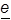
 mit der Gegenwahrscheinlichkeit 1-w eintritt. Der Entscheider muß angeben, bei welcher Wahrscheinlichkeit w* er indifferent ist zwischen dem sicheren Ergebnis eas und der Lotterie. Der Nutzenwert U(eas) wird gleich dieser Wahrscheinlichkeit gesetzt:      U(eas) = w*. Das B. macht keine Aussage über die Gestalt der Nutzenfunktion U, diese ist abhängig vom Entscheider. Demgemäß ist das B. ein Entscheidungsprinzip und wird erst dann zu einem Entscheidungskriterium, wenn die Nutzenfunktion eindeutig spezifiziert ist. Das B. gibt aber konkrete Anweisungen zur empirischen Bestimmung der Nutzenfunktion. Das B. wurde 1738 von D. Bernoulli formuliert und 1944 von J. v. Neumann und O. Morgenstern aufgegriffen und axiomatisch begründet.