|
Entscheidungstheorie
Inhaltsübersicht
I. Übersicht
II. Problemstrukturierung
III. Entscheidung bei mehrfachen Zielen
IV. Entscheidung unter Risiko
V. Weitere Hinweise
I. Übersicht
Die Entscheidungstheorie (englisch: decision analysis) ist eine Disziplin mit präskriptiver Orientierung, die Personen beim Treffen komplexer Entscheidungen unterstützen will. Sie enthält ein Arsenal von Konzepten und Methoden von genereller Anwendbarkeit ‐ beispielsweise im Management, in der Medizin, den Ingenieurwissenschaften oder der Politik. Ihre Daseinsberechtigung beruht auf der Beobachtung, dass auch schwerwiegende Entscheidungen häufig intuitiv oder auf der Basis unzureichender und unsystematischer Analyse getroffen werden. Psychologen, die tatsächliches Entscheidungsverhalten untersucht haben, beschreiben eine große Anzahl systematisch auftretender Wahrnehmungs- und Urteilsverzerrungen.
Die Entscheidungstheorie zielt auf rationalere Entscheidungen. Rationalität kann zum einen als prozedurale Rationalität verstanden werden und zielt darauf, die der Bedeutung der jeweiligen Entscheidung angemessene Sorgfalt bei der Wahl des Entscheidungskontextes und bei der Informationssuche ‐ betreffend die eigenen Ziele, die Alternativen, die Risiken und Chancen ‐ aufzuwenden (Phillips, L.D. 1982). Eine „ optimale “ Entscheidung ist immer nur in einem mehr oder weniger adäquaten Modell der realen Situation optimal, ein Tatbestand, den Simon als „ bounded rationality “ bezeichnet hat (Simon, H.A. 1957). Der Grad der prozeduralen Rationalität ist niemals objektiv messbar. Zum zweiten bedeutet Rationalität Konsistenz. Die Informationen, auf denen eine Entscheidung basiert wird, dürfen nicht im Widerspruch zu Postulaten rationalen Verhaltens stehen, die der Entscheider als solche anerkennt, wie z.B. die Regeln der Wahrscheinlichkeitsrechnung oder die Transitivität von Präferenzen.
II. Problemstrukturierung
Grundlegendes Paradigma der Entscheidungstheorie ist die Zerlegung komplexer Probleme in einfachere Teilprobleme. Voraussetzung für eine rationale Entscheidung ist daher eine angemessene Problemstrukturierung. Jedes Entscheidungsproblem lässt sich in vier Teilmodelle zerlegen: (1) Ziele und Präferenzen, (2) Alternativen, (3) Umwelteinflüsse und (4) Konsequenzen.
1. Ziele und Präferenzen
Ziele und Präferenzen drücken aus, was ein Entscheider erreichen will, und sind notwendig subjektiv. Die Entscheidungstheorie erhebt keinen normativen Anspruch und wertet Präferenzen nicht.
Ein Ziel besteht aus einer Zielvariablen und ‐ gewöhnlich ‐ einer Optimierungsrichtung, z.B. Maximierung des Gewinns oder Minimierung der Schadstoffemission. Im einfachsten Fall spielt nur ein Ziel eine Rolle. In den meisten wichtigen Entscheidungen sind jedoch mehrere Ziele von Belang, die sich auf die gewünschten Eigenschaften von Problemlösungen beziehen, etwa Fähigkeiten von Bewerbern, Umweltverträglichkeit von Produkten oder Sozialverträglichkeit von Desinvestitionen.
Die Generierung eines Zielsystems ist ein wichtiger und in der Praxis allzu oft vernachlässigter Schritt (Keeney, R.L. 1992). An ein Zielsystem sind einige Anforderungen zu stellen. Die Ziele sollten fundamental sein in dem Sinne, dass nicht ein Ziel lediglich Instrumentalcharakter zur Erreichung eines anderen Ziels hat; dies würde zu Doppelbewertungen führen. Sie sollten durch Attribute operationalisiert werden, die eine eindeutige Messung erlauben. Die hierarchische Anordnung der Ziele, d.h. die Etablierung von Oberziel-Unterziel-Relationen, erleichtert die Prüfung des Zielsystems auf Vollständigkeit und Nichtredundanz.
Sodann muss der Entscheider seine Präferenzen bezüglich dieser Ziele bestimmen, sodass die Bewertung multivariabler und/oder unsicherer Konsequenzen möglich wird. Die Präferenzen werden durch Wertfunktionen (bei Sicherheit) bzw. Nutzenfunktionen (bei Unsicherheit) repräsentiert. Inwieweit sich die Präferenzen durch (z.B. additive oder multiplikative) Aggregation univariabler Wert- bzw. Nutzenfunktionen darstellen lassen, muss durch geeignete Tests geklärt werden. Sowohl für die Generierung von Einzelwert- bzw. Einzelnutzenfunktionen als auch für die Bestimmung der Skalierungsfaktoren ( „ Gewichte “ ) wurden Verfahren entwickelt (Keeney, R.L./Raiffa, H. 1976).
Bei mehrperiodigen Konsequenzen kann die Ermittlung von Zeitpräferenzen geboten sein. Gruppenentscheidungen enthalten das Problem der Aggregation von Einzel- zu Gruppenpräferenzen.
2. Alternativen
Entscheidung ist die Auswahl einer Alternative aus einer Menge sich gegenseitig ausschließender Alternativen. Es kann sich um einstufige Alternativen handeln, z.B. die Auswahl einer Produktionsanlage oder eines Softwarepakets. Mehrstufige Alternativen (Strategien) enthalten neben einer Anfangsentscheidung auch bedingte Anweisungen für weitere Entscheidungen in Abhängigkeit von späteren Ereignissen.
3. Umwelteinflüsse
Neben der eigenen Entscheidung können auch nichtbeeinflussbare Faktoren die Handlungskonsequenzen mitbestimmen, z.B. die Reaktion von Nachfragern oder die künftige Steuergesetzgebung. Man spricht von Entscheidungen unter Sicherheit, wenn der Entscheider diese Ereignisse mit (hinreichender) Sicherheit vorhersagen zu können glaubt. Dementsprechend bedeutet Unsicherheit oder ‐ hier synonym gebraucht ‐ Risiko, dass eine Entscheidung zu unterschiedlichen Konsequenzen führen kann, je nachdem, welches Ereignis eintritt. Dann ist zu versuchen, die Eintrittswahrscheinlichkeiten der Ereignisse zu bestimmen.
Die Entscheidungstheorie geht von einem subjektiven Wahrscheinlichkeitsbegriff aus. Subjektive Wahrscheinlichkeiten sollten zwar durch relevante und nachprüfbare Informationen begründet sein, enthalten aber immer ein subjektives Element, sodass ihre „ Richtigkeit “ nicht abschließend beurteilt werden kann.
Wahrscheinlichkeiten müssen, ebenso wie Präferenzen, durch Befragungsprozesse von Personen gebildet, stabilisiert und explizit gemacht werden (elicitation). Hierfür wurden Methoden entwickelt (Spetzler, C.S./Staël von Holstein, C.A.S. 1975), die um so wichtiger sind, als psychologische Studien schwerwiegende Defekte der menschlichen Fähigkeiten bei der Bezifferung und Verknüpfung von Wahrscheinlichkeiten offen gelegt haben (Kahneman, D./Slovic, P./Tversky, A. 1982; Hastie, R./Dawes, R. M. 2001; Bazerman, M.H. 2002).
4. Konsequenzen
Eine Konsequenz ist durch die Ausprägungen der Zielvariablen definiert, die als Folge der Entscheidung und der Umwelteinflüsse eintreten. Bei Sicherheit führt jede Entscheidung zu einer eindeutigen Konsequenz, bei Unsicherheit sind mehrere Konsequenzen alternativ möglich. Es gilt für jede Konsequenz die Ausprägungen aller Zielvariablen zu ermitteln. Dazu muss unter Umständen ein Wirkungsmodell konstruiert werden. Beispielsweise ist die Auswirkung einer Kapazitätsentscheidung auf den Gewinn nicht unmittelbar ersichtlich, sondern erst durch ein Optimierungsmodell, das die optimale Aufteilung der Kapazität auf mehrere Produkte bestimmt, zu ermitteln.
5. Rekursive Modellierung
Die vier Module können selten sukzessiv erstellt werden. Sie beeinflussen sich gegenseitig; z.B. führt oft die Ausweitung der Alternativenmenge zum Erkennen wichtiger Eigenschaften der neuen Alternativen, sodass auch die Menge der Ziele sich vergrößert. Es handelt sich daher um einen rekursiven Prozess, der dann beendet wird, wenn der Entscheider glaubt, das Problem hinreichend vollständig und exakt beschrieben zu haben.
Während des Prozesses sind wiederholt Vor-Entscheidungen zu treffen, z.B. darüber, welches Problem zu lösen ist (Erweiterung oder Einschränkung des Entscheidungskontexts), die Suche nach weiteren Alternativen oder die Berücksichtigung von zusätzlichen Informationen.
6. Einflussdiagramme
Ein Hilfsmittel zur kompakten Darstellung von Entscheidungsproblemen ist das Einflussdiagramm (Oliver, R.M./Smith, J.O. 1990). Es stellt Entscheidungen (rechteckige Symbole), Umwelteinflüsse (Ovale) und Ziele (Rauten) dar; Pfeile bedeuten kausale oder stochastische Einflüsse. Abb. 1 zeigt ein Beispiel. Zunächst ist zu entscheiden, ob eine Produktentwicklung fortgesetzt oder abgebrochen werden soll. Bei Fortsetzung ist zu einem späteren Zeitpunkt über die Produktionskapazität zu entscheiden. Externe Einflüsse sind der technische Erfolg, das Marktpotenzial, das eventuelle Auftreten eines Konkurrenzprodukts etc. Zielvariablen sind der Gewinn und das spezifische Know-how, welches das Unternehmen durch die Entwicklung und die Produktion erlangen würde. Einflussdiagramme eignen sich zur Unterstützung der Kommunikation zwischen Entscheidungsträgern und zur Prüfung, ob alle wesentlichen Elemente des Entscheidungsmodells berücksichtigt werden.

Abb. 1: Einflussdiagramm
III. Entscheidung bei mehrfachen Zielen
Viele Entscheidungsprobleme lassen sich adäquat als Entscheidung bei multiplen Zielen und sicheren Erwartungen modellieren, z.B. die Wahl zwischen mehreren bekannten Bewerbern um eine Position. Für die Bewertung der Alternativen wird eine multiattributive Wertfunktion v(x1, x2, ... , xk) gebildet, welche die Präferenzen des Entscheiders bezüglich der Ausprägungen der Zielvariablen X1 bis Xk ausdrückt. Der Buchstabe v steht für value.
Eine wegen ihrer Einfachheit häufig benutzte Wertfunktion ist die additive:
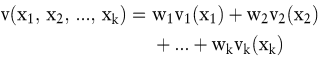
Hierin bedeutet vi(xi) die (Einzel)wertfunktion bezüglich der Zielvariablen Xi. Alle Einzelwertfunktionen sind auf das Intervall [0, 1] normiert. Die wi sind Gewichtungsfaktoren zwischen null und eins, die die relative Bedeutung der Ziele repräsentieren; Es gilt w1 + w2 + ... + wk = 1. In Tab. 1 ist eine Situation mit drei Alternativen (a, b, c) und drei Zielvariablen (X1, X2, X3) dargestellt. Die Eintragungen in den Zellen bedeuten die Ausprägungen der Zielvariablen bei den einzelnen Alternativen.

Tab. 1: Entscheidungsmatrix für drei Alternativen und drei Ziele bei Sicherheit
Das additive Wertmodell repräsentiert die Präferenzen des Entscheiders genau dann, wenn dieser bezüglich der Zielvariablen wechselseitige Präferenzunabhängigkeit empfindet. Das bedeutet: Die Präferenz zwischen zwei beliebigen Alternativen a und b, die sich nur hinsichtlich einer (beliebigen) Teilmenge der Zielvariablen unterscheiden, hängt nicht davon ab, welche Ausprägungen die Zielvariablen der Restmenge haben. Ist die wechselseitige Präferenzunabhängigkeit nicht gegeben, kann evtl. auf andere Aggregationsmodelle zurückgegriffen werden. Häufig lässt sich jedoch durch eine Redefinition des Zielsystems die Bedingung der wechselseitigen Präferenzunabhängigkeit herstellen.
Die Gewichtungsfaktoren werden präferenzbasiert bestimmt. Zweckmäßigerweise vergleicht der Entscheider Alternativen, die sich nur in zwei Kriterien Xi und Xj unterscheiden, bei den übrigen Kriterien jedoch gleiche Ausprägungen aufweisen. Die Ausprägungen von Xi und Xjwerden so lange variiert, bis Indifferenz gilt (Tradeoff-Verfahren). Dann hat man eine lineare Gleichung in den Gewichtungsfaktoren wiund wj. Bei n Zielvariablen lassen sich aus n – 1 Indifferenzaussagen zusammen mit der Normierung der Gewichtsumme auf eins die Gewichte ausrechnen.
Intuitive Empfindungen über die „ Wichtigkeit “ von Zielen führen zu falschen Entscheidungen, da ein Zielgewicht nicht eine Eigenschaft des Ziels ist, sondern von dem Wertunterschied zwischen der schlechtesten und der besten im Modell angenommenen Ausprägung abhängt.
In der Praxis sind additive Bewertungsverfahren verbreitet, häufig unter dem Namen „ Scoringmodell “ oder „ Nutzwertanalyse “ . Dabei wird in aller Regel die genannte Gültigkeitsvoraussetzung nicht beachtet, und die Zielgewichtung wird nicht in nachvollziehbarer Weise aus Präferenzen abgeleitet. Die häufigsten Anwendungsfehler sind bei Weber/Krahnen/Weber dargestellt (Weber, M./Krahnen, J.P./Weber, A. 1995).
IV. Entscheidung unter Risiko
Wenn mindestens eine der Alternativen keine sichere Konsequenz hat, liegt Entscheidung unter Risiko vor. Die endgültige Konsequenz wird auch von externen Einflüssen bestimmt. Eine Kombination mehrerer Einflüsse heißt Szenario. Die Situation kann wieder durch eine Entscheidungsmatrix, wie in Tab. 2 illustriert, dargestellt werden.

Tab. 2: Entscheidungsmatrix für drei Alternativen und drei Szenarien
Hier bedeutet z.B. c1adie Konsequenz, die eintrifft, wenn Alternative a gewählt wird und das Szenario s1 eintritt. Die Konsequenzen sind bei einfacher Zielsetzung Ausprägungen der einen Zielvariablen, bei mehrfacher Zielsetzung sind sie Vektoren von mehreren Zielvariablen.
Eine andere, jedoch äquivalente Darstellung von Entscheidungen bei Risiko ist der Entscheidungsbaum (Abb. 2, Flexible Planung). Entscheidungen sind hier als Vierecke, unsichere Ereignisse als Kreise dargestellt. Zahlen an den Ereignissen bedeuten deren Wahrscheinlichkeiten. Entscheidungsbäume eignen sich besonders zur Darstellung mehrstufiger Entscheidungen.

Abb. 2: Entscheidungsbaum
Der Entscheidungsbaum in Abb. 2 zeigt das Problem eines Lieferanten, eine umstrittene Forderung von 100 Geldeinheiten durch Prozess einzuklagen oder dem Schuldner einen Verzicht von 50 % anzubieten. Der Ausgang des Prozesses kann Sieg, Niederlage oder ein gerichtlicher Vergleich von 50 % sein. Die subjektiven Wahrscheinlichkeiten sind an den Ästen angegeben. Im Fall eines eigenen Vergleichsangebots ist entweder mit Annahme durch den Schuldner, Ablehnung oder einem Gegenvorschlag von 25 % der Forderung zu rechnen. Der Lieferant kann, sofern der Schuldner den Vergleichsvorschlag nicht annimmt, immer noch einen Prozess führen. Die an den Endpunkten des Baums eingetragenen Werte sind die Konsequenzen, ausgedrückt in Geldeinheiten.
Zur optimalen Lösung von Entscheidungsproblemen unter Risiko wird auf das Kriterium der Maximierung des Nutzenerwartungswertes zurückgegriffen. Es besagt: Wähle diejenige Alternative, die die höchste mit den Wahrscheinlichkeiten gewichtete Summe des Nutzens der möglichen Konsequenzen besitzt. Im Beispiel der Entscheidungsmatrix (Tab. 2) hat die Alternative a den Nutzen

Dieses Prinzip wird im deutschen Sprachraum nach dem Mathematiker Daniel Bernoulli, D. (18. Jh.) als Bernoulliprinzip bezeichnet. International wird es dagegen John von Neumann und Oskar Morgenstern zugeschrieben, die es erstmals axiomatisch begründet haben (von Neumann, J./Morgenstern, O. 1947). Die Nutzenfunktion u(x) über der Zielvariablen X – hierbei steht u für utility – muss nach bestimmten Vorschriften ermittelt werden, die garantieren, dass das Kriterium des Nutzenerwartungswertes sich aus wenigen plausiblen Axiomen als rational begründen lässt.
Eine Nutzenfunktion u(x) ist nicht notwendig mit der Wertfunktion v(x) des gleichen Entscheiders über den gleichen Bereich der Zielvariablen X identisch. Während Wertfunktionen aus Befragungen hervorgehen, die die Präferenzen des Entscheiders gegenüber sicheren Ausprägungen der Zielvariablen ausdrücken, beruhen Nutzenfunktionen auf Präferenzen gegenüber Lotterien (Wahrscheinlichkeitsverteilungen von Zielvariablen) und enthalten deshalb auch Informationen über die Risikoeinstellung des Entscheiders.
Risikoneutralität bezüglich einer unsicheren Zielvariablen liegt vor, wenn der Entscheider indifferent zwischen einer Wahrscheinlichkeitsverteilung über dieser Variablen und deren Erwartungswert ist. Ein risikoneutraler Entscheider würde also indifferent zwischen einem Münzwurf, bei dem er mit je 50% Wahrscheinlichkeit null oder 1.000 Eur gewinnt, und einem sicheren Gewinn von 500 Eur sein. Risikoscheu dagegen bedeutet, dass das Sicherheitsäquivalent geringer als der Erwartungswert ist. Der Entscheider wäre z.B. indifferent zwischen der Lotterie und einem sicheren Gewinn von 350 Eur. Bei Risikoneutralität ist diejenige Alternative optimal, die den Erwartungswert der Zielvariablen maximiert bzw. minimiert; der Nutzen ist eine lineare Funktion der Zielvariablen. Im Beispiel der Abb. 2 weist die Strategie „ Prozess führen “ mit 61,5 Geldeinheiten den höchsten Erwartungswert auf und ist bei Risikoneutralität optimal.
Eine Nutzenfunktion kann wie folgt konstruiert werden. Sei willkürlich der Nutzen des geringsten Gewinns (hier z.B. null Euro) gleich null gesetzt, der Nutzen der höchsten Gewinns (hier 1.000 Euro) gleich eins. Bei einer Lotterie mit gleichen Chancen beträgt deren Nutzenerwartungswert 0,5 0 + 0,5 1 = 0,5. Empfindet der Entscheider einen sicheren Gewinn von 350 Euro als der Lotterie gleichwertig, so ist u(350) = 0,5. Damit ist ein Punkt der Nutzenfunktion bestimmt. Durch weitere Indifferenzaussagen über Lotterien und deren Sicherheitsäquivalente lassen sich zusätzliche Punkte bestimmen, die dann durch eine durchgehende Kurve angenähert werden können (Abb. 3). Der konkave Verlauf der Funktion repräsentiert Risikoscheu im gesamten Wertebereich.
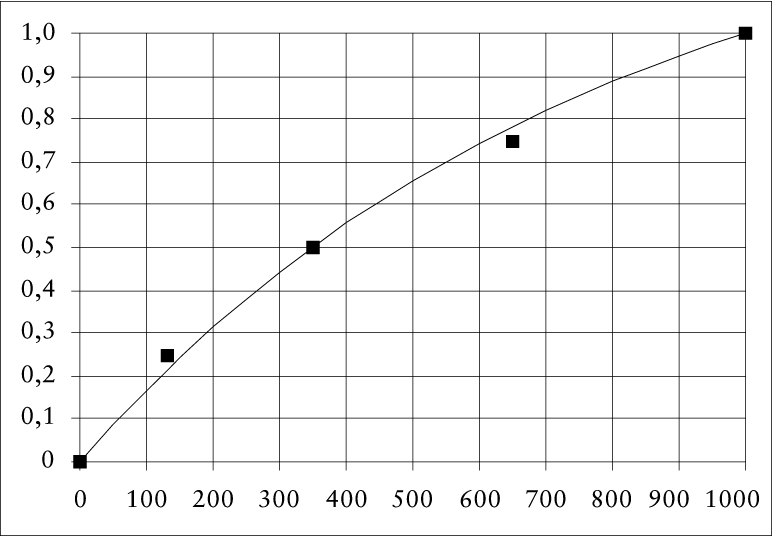
Abb. 3: Bestimmung einer Nutzenfunktion
V. Weitere Hinweise
Als Lehrbücher der Entscheidungstheorie seien Bamberg/Coenenberg, Clemen, Eisenführ/Weber und Laux genannt (Bamberg, G./Coenenberg, A.G. 2004; Clemen, R.T. 1996; Eisenführ, F./Weber, M. 2003 und Laux, H. 2005). Populärwissenschaftliche Darstellungen der Grundgedanken der Entscheidungstheorie sind bei Hammond/Keeney/Raiffa, Keeney und Russo/Schoemaker zu finden (Hammond, J.S./Keeney, R.L./Raiffa, H. 1999; Keeney, R.L. 1992; Russo, J.E./Schoemaker, P.J.H. 1989). Psychologische Erkenntnisse über fehlerhaftes intuitives Entscheidungsverhalten sind leicht verständlich bei Bazerman, Hastie/Dawes, Jungermann/Pfister/Fischer und Plous dargestellt (Bazerman, M.H. 2002; Hastie, R./Dawes, R.M. 2001; Jungermann, H./Pfister, H.-R./Fischer, K. 1998; Plous, S. 1993).
Zeitschriften mit entscheidungstheoretischem Fokus sind u.a. Decision Sciences, Interfaces, Journal of Behavioral Decision Making, Journal of Risk and Uncertainty, Journal of Multicriteria Decision Analysis, Journal of Group Decision and Negotiation und Management Science.
Der Nutzen entscheidungstheoretischer Konzepte hat sich durch die gestiegene Rechenleistung der Computer stark erhöht. Eine beträchtliche Menge kommerzieller Programme zur Entscheidungsanalyse steht dem Anwender zur Verfügung. Das Lehrbuch von Kirkwood enthält Anwendungsbeispiele unter Verwendung der Tabellenkalkulations-Software Microsoft Excel (Kirkwood, C.W. 1997).
Aktuelle Informationen über die Entwicklung des Gebietes, Tagungen, Software etc. sind über die Internet-Adresse der Decision Analysis Society zu bekommen: http://faculty.fuqua.duke.edu/daweb/.
Literatur:
Bamberg, Günter/Coenenberg, Adolf G. : Betriebswirtschaftliche Entscheidungslehre, München, 12. A., 2004
Bazerman, Max H. : Judgment in managerial decision making, New York, 5. A., 2002
Clemen, Robert T. : Making hard decisions, Pacific Grove, Ca., 2. A., 1996
Eisenführ, Franz/Weber, Martin : Rationales Entscheiden, Berlin et al., 4. A., 2003
Hammond, John S./Keeney, Ralph L./Raiffa, Howard : Smart choices. A practical guide to making better decisions, Cambridge, Ma. 1999
Hastie, Reid/Dawes, Robyn M. : Rational choice in an uncertain world, Thousand Oaks, Ca. 2001
Jungermann, Helmut/Pfister, Hans-Rüdiger/Fischer, Katrin : Die Psychologie der Entscheidung, Heidelberg 1998
Kahneman, Daniel/Slovic, Paul/Tversky, Amos : Judgment under Uncertainty: Heuristics and Biases, Cambridge, Ma. 1982
Keeney, Ralph L. : Value focused thinking, Cambridge, Ma. 1992
Keeney, Ralph L./Raiffa, Howard : Decisions with Multiple Objectives: Preferences and Value Tradeoffs, New York 1976
Kirkwood, Craig W. : Strategic decision making. Multiobjective decision analysis with spreadsheets, Belmont 1997
Laux, Helmut : Entscheidungstheorie, Berlin et al., 6. A., 2005
Phillips, Larry D. : Requisite Decision Modeling: A Case Study, in: Journal of Operational Research Society, Jg. 33, 1982, S. 303 – 311
Oliver, R.M./Smith, J.Q. : Influence diagrams, belief nets and decision analysis, hrsg. v. , New York 1990
Plous, Scott : The psychology of judgement and decision making, New York 1993
Russo, J. Edward/Schoemaker, Paul J. H. : Decision traps. The ten barriers to brilliant decision-making & how to overcome them, New York 1989
Simon, Herbert A. : Models of Man, New York 1957
Spetzler, C.S./Staël von Holstein, C.A.S. : Probability encoding in decision analysis, in: Jg. 22, Management Science, 1975, S. 340 – 358
von Neumann, John/Morgenstern, Oskar : Theory of Games and Economic Behavior, Princeton, 2. A., 1947
Weber, Martin/Krahnen, Jan P./Weber, Adelheid : Scoring-Verfahren – häufige Anwendungsfehler und ihre Vermeidung, in: DB, 1995, S. 1621 – 1626
|