Verteilung

in der Deskriptiven Statistik die empirisch beobachtete Häufigkeitsverteilung; in der Wahrscheinlichkeitstheorie ist Verteilung die Zuordnung von Wahrscheinlichkeiten zu den Ereignissen von Zufallsexperimenten. Man spricht deshalb von der Wahrscheinlichkeits-V. Sie entspricht der V. von Zufallsvariablen . Für eine einzelne Zufallsvariable X können die Wahrscheinlichkeiten der Ereignisse


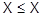
 als Fundament benutzt werden. Man erhält daraus die V.-sfunktion der Zufallsvariablen 


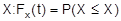
. Die V.-funktionen diskreter und stetiger Zufallsvariabler unterscheiden sich (s. Zufallsvariable). Die V. ist eindimensional, wenn sie sich nur auf eine einzige Zufallsvariable bezieht; sie ist mehrdimensional, wenn sie sich auf mehrere Zufallsvariablen bezieht. Zu den V. s. z.B. Binomial-Verteilung , Normal-Verteilung ,  Standardnormal-Verteilung , Chi-quadrat-Verteilung , Student-Verteilung In der Verteilungstheorie werden die Einkommens-Verteilung, Vermögens-V., Primär-V. usw. untersucht.