Ereignis, Ereignisse

I. in der Wahrscheinlichkeitsrechnung:
1. Elementar-E. sind die möglichen E. eines Versuchs, z.B. die erzielbaren Augenzahlen beim Würfelwurf. Die Menge aller möglichen E. heißt Grundraum oder E.-raum und wird mit W bezeichnet. Den Grundraum W nennt man auch das sichere E., die leere Menge Æ das unmögliche E.
2. E. ist die endliche oder unendliche Menge von Elementar-E., z.B. das E. A beim Würfelwurf, eine gerade Augenzahl zu werfen: A = { 2, 4, 6} . Bezeichnen An, E., so bedeuten


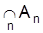
 das gleichzeitige Eintreffen sämtlicher


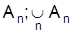
 das Eintreffen mindestens eines


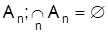
 Unvereinbarkeit der An , man spricht dann von disjunkten E. E. A und B heißen unabhängig, wenn für die Wahrscheinlichkeit ihres gleichzeitigen Eintretens der Multiplikationssatz P (A Ç B) = P (A) * P (B) gilt. Für P(B) ¹ 0 ist dies gleichbedeutend damit, daß die bedingte Wahrscheinlichkeit P (A|B) (für das E. A bei Vorliegen von B) mit der Wahrscheinlichkeit P(A) übereinstimmt. Zwei Zufallvariable X und Y werden unabhängig genannt, wenn für alle zugehörenden E. A, B gilt: P(X Î A, Y Î B) = P(X Î A) * P(Y Î B). II. in der Netzplantechnik Eintreten eines definierten Zustandes im Prozeßablauf.