Indifferenzkurvenanalyse

1. Indifferenzkurve.
1. 1. Definition. Theoretische Grundlage der I. ist die Existenz einer Präferenzordnung über dem Güterraum


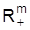
. Ist diese stetig, so existiert eine ordinale Nutzenfunktion (Nutzenindex-, Präferenzfunktion) U = U(q1, ..., qm), deren Argumente die Mengen der m Güter sind. Ist m = 2, lassen sich Indifferenzkurven aus dieser Nutzenfunktion ableiten. Diese geben alle Mengenkombinationen der beiden Güter an, die den gleichen Nutzen aufweisen. Figur 1 enthält eine Indifferenzkurve für die beiden Güter 1 und 2; sie weist für alle zugehörigen Mengenkombinationen den Nutzen


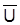
 auf.                        



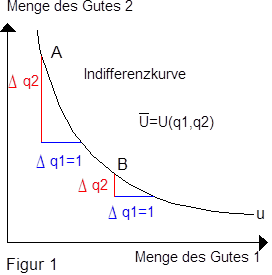
1. 2 Eigenschaften. Eine Indifferenzkurve ist typischerweise streng konvex. Hierin kommt das Gesetz der abnehmenden Grenzrate der Substitution zum Ausdruck. Unter Rate der Substitution des Gutes 2 in bezug auf Gut 1 versteht man jene Menge des Gutes 2, die je zusätzlicher Einheit des Gutes 1 aufgegeben werden muß, damit der Nutzen konstant bleibt; in Figur 1 also das Verhältnis |Dq2 / Dq1|. Wird die zusätzliche Einheit des Gutes 1 infinitesimal klein, so wird aus der Rate der Substitution die Grenzrate der Substitution. Sie entspricht dem (absoluten) Anstieg der Indifferenzkurve in einem Punkt, d.h., sie ist gleich |Dq2 / Dq1|. Substituiert man fortlaufend Gut 2 durch Gut 1, d.h. geht man in Figur 1 vom Punkt A zum Punkt B über, so nimmt die Grenzrate der Substitution ab; dies ist die Aussage des Gesetzes der abnehmenden Grenzrate der Substitution. In ihm kommt inhaltlich zum Ausdruck, daß es immer schwieriger wird, den Zugang eines Gutes durch Verminderung der Menge eines anderen Gutes so auszugleichen, daß der Nutzen konstant bleibt. Indifferenzkurven lassen sich auch direkt aus einer Präferenzordnung ableiten. Ist die Präferenzordnung streng konvex, dann muß auch eine aus ihr abgeleitete Indifferenzkurve streng konvex sein. Durch jeden Punkt des Koordinatensystems der Figur 1 geht eine Indifferenzkurve. Da normalerweise unterstellt wird, daß größere Gütermengen zu höherem Nutzen führen (Nichtsättigung), weist eine Indifferenzkurve einen umso höheren Nutzenindex auf, je weiter sie vom Koordinatenursprung entfernt liegt. Diese Indifferenzkurven können sich nicht schneiden, jedoch können Schnittpunkte mit der Abszisse und der Ordinate existieren.
2. Analyseverfahren. Mit Hilfe einer Schar von Indifferenzkurven ist es möglich, für m = 2 das Haushaltsoptimum eines privaten Haushalts (Haushalt,
1.) zu bestimmen, vgl. Figur
2.                        


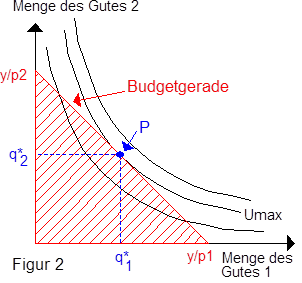
Bei gegebenen Preisen p1 und p2 der beiden Güter 1 und 2 sowie bei gegebenem Einkommen y, sind jene Mengen beider Güter zu bestimmen, die zu einem maximalen Nutzen führen. Haushaltseinkommen und Güterpreise legen die Budgetgerade fest. Diese begrenzt zusammen mit den Achsen des Koordinatensystems den Konsumraum


 ; der Haushalt kann nur aus den Güterbündeln wählen, die innerhalb des schraffierten Gebiets der Figur 2 einschließlich der Begrenzungslinien liegen. Wg. der strengen Konvexität der Indifferenzkurven existiert ein Tangentialpunkt zwischen der Budgetgeraden und einer Indifferenzkurve; dieser Tangentialpunkt (Punkt P in Figur 2) gibt den optimalen Konsumplan oder das Haushaltsoptimum an. Nur die durch P festgelegten Konsumgütermengen


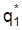
 und


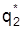
 führen bei gegebenem Einkommen und gegebenen Güterpreisen zu einem maximalen Nutzen Umax. Der Lösungspunkt P ändert sich nicht, wenn die zugrundeliegende ordinale Nutzenfunktion einer beliebigen positiven, monotonen Transformation unterzogen wird. Bei einer solchen Transformation änderten sich weder Lage noch Gestalt der Indifferenzkurven, lediglich ihre Nutzenindizes würden unter Beibehaltung der Reihenfolge andere Werte annehmen. Durch Variation eines Preises bzw. des Einkommens lassen sich die Preis -Konsum-Kurve sowie die Einkommen -Konsum-Kurve (Engel-Kurve) ableiten, vgl. auch Einkommens - und Substitutionseffekt. Für m > 2 sind die gleichen Überlegungen analog durchzuführen. Der optimale Konsumplan wird jedoch analytisch mit Hilfe eines Lagrange-Ansatzes zu bestimmen sein.
3. Weitere Anwendungen. Die I. wird auch zur Lösung anderer Entscheidungsprobleme eines Haushalts angewandt, z.B. zur Bestimmung des Arbeitsangebots (s. Faktorangebot des Haushalts). In der Makroökonomik bedient man sich ebenfalls der Indifferenzkurvenanalyse. Hier werden die Indifferenzkurven aus einer sozialen Wohlfahrtsfunktion (Wohlfahrtsökonomik) abgeleitet und dienen z.B. dem Nachweis von Vorteilen des internationalen Handels.

Literatur: H. Herberg, Preistheorie.
2. A., Stuttgart, Berlin, Köln, Mainz 1989. H. R. Varian, Mikroökonomie.
2. A., München, Wien 1992. J. Schumann, Grundzüge der mikroökonomischen Theorie.
6. A., Berlin, Heidelberg 1993.