Nash-Cournot-Gleichgewicht

siehe unter Cournot-Nash-Gleichgewicht  Oligopol -Preisbildungsmodell , bei dem jede Unternehmung das Angebot des Konkurrenten als fix betrachtet. Im Falle des Dyopols seien q1 (q2) die Funktion, welche die optimale Outputwahl der Unternehmung 1 bei gegebenem Output der Unternehmung 2 beschreibt, und q2 (q1) die analoge Funktion für Unternehmung
2. Man kann diese "Reaktionskurven" in eine (q1, q2)-Ebene zeichnen (siehe Abbildung). Ein Cournot-Nash-Gleichgewicht ist nun einfach eine Kombination (q1*, q2*), die auf beiden Reaktionskurven der Unternehmungen liegt (d.h. in deren Schnittpunkt).                        


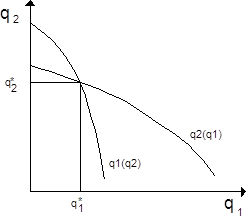
Man kann auch annehmen, daß jede Unternehmung den Preis der anderen Unternehmung als fix gegeben nimmt. Da es sich um ein homogenes Gut (Gut) handelt, müssen beide im Gleichgewicht den gleichen Preis verlangen. Das Ergebnis lautet, daß das N. ein Konkurrenzgleichgewicht ist: Der Preis ist gleich den Grenzkosten (Kosten).