Normalverteilung

Die Normalverteilung (auch: Gauß-Vertei­lung, „ Glockenkurve“) erhält ihre herausra­gende Bedeutung dadurch, dass sie und ihre „Abkömmlinge“ zumindest approximativ vielen Verfahren der Inferenzstatistik zu­grunde liegen. Sie ist stetig, symmetrisch, ein- gipflig und gekennzeichnet durch 2 Parame­ter; |l in der Mitte („arithmetisches Mittel“, „Median“ und „Modus“ zugleich) und der Standardabweichung <7. Setzt man - im Ein­klang mit den wahrscheinlichkeitstheoreti­schen Axiomen - die gesamte von der Nor- malverteilungskurve umschlossene Fläche gleich 1 (oder 100), so kann der Anteil der je­weils umschlossenen Fläche in u-Einheiten berechnet werden. (So umschließt 1 <T 68,3 %, 1,96(7 95%, 2a 95,5% usw.) Die mit ji = 0 und ct= 1 gegebene Normalverteilung be­zeichnet man als Standard-Normalver- teilung. Die vielfach wiedergegebenen Tafeln beziehen sich hierauf (wobei allerdings die Art der Tabellierung durchaus unterschied­lich sein kann). Die Standardisierung empiri­scher Werte erfolgt durch die sog. z-Trans- formation: z = (x-x)/s.         

in theoretischer und praktischer Hinsicht wichtigste stetige Häufigkeitsverteilung der Statistik . Sie besitzt die Verteilungsdichte                        


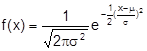
Dabei ist m der Erwartungswert , s2 die Varianz der normalverteilten Zufallsvariablen; sie wird mit N (m,s2) bezeichnet, die Standardnormalverteilung mit N(0,1). Bei graphischer Darstellung ergibt die Dichte der N. eine Glockenkurve, die symmetrisch zur Geraden x = m  ist. Der Erwartungswert m fällt zusammen mit dem Modalwert und dem Median . Die Glockenkurve hat Wendepunkte bei m + s und  m - s .                        


Unter gewissen Voraussetzungen eignet sich die N. zur Approximation vieler theoretischer Verteilungen wie der Binomial -, Hypergeometrischen oder  Chi -Quadrat-Verteilung.