Varianz

(A)  (Definition) entspricht dem   Erwartungswert der quadratischen Abweichungen einer Zufallsvariablen von ihrem Erwartungswert. (B)  (Statistik, Wahrscheinlichkeitsrechnung).
(1) in der beschreibenden Statistik, siehe dazu   Statistik (mit Literaturangaben) und   Empirische Momente;
(2) in der Wahrscheinlichkeitsrechnung, siehe da­zu   Wahrscheinlichkeitsrechung und   Zufallsvariable.


1. Gebräuchliches Streuungsmaß einer statistischen Reihe bzw. Häufigkeitsverteilung. Sind


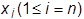
 Ausprägungen eines metrischen Merkmals einer statistischen Reihe gegeben, so ist die V. definiert durch                        


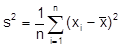
, als Summe der quadratischen Abweichungen der Merkmalswerte vom arithmetischen Mittel


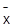
bezogen auf die Gesamtzahl n der Merkmale.
2. Grundbegriff der Wahrscheinlichkeitstheorie. Sind


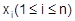
 die Ausprägungen einer diskreten Zufallsvariablen X und f(xi) die zugehörigen Wahrscheinlichkeiten, so ist          Var (X) = E [(X - EX)2 =           


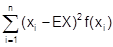
      die V. der Zufallsvariablen X. Für eine stetige Zufallsvariable X mit Dichtefunktion f(x) gilt          Var (X) = E [(X - EX)2 =                   


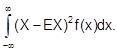
EX = Erwartungswert der Zufallsvariablen X.