Elastizitäten

In den Wirtschaftswissenschaften wird häufig danach gefragt, wie sich eine abhängige Variable (y) (Variable) ändert, wenn eine mit ihr funktional verbundene unabhängige Variable (x) (Variable) variiert. Um den Einfluß der für die Größen gewählten Dimensionen oder Maßeinheiten auszuschalten, erweist es sich als zweckmäßig, nicht die absoluten Veränderungen  (Dx, Dy) zueinander in Beziehung zu setzen, sondern die relativen, auf die Niveauwerte bezogenen Veränderungen. Einen Quotient aus so gebildeten relativen Veränderungen bezeichnet man als E. Grundsätzlich lassen sich aus jeder funktionalen Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen die zugehörigen E. bilden. Sind zwei Variable durch eine stetige Funktion verbunden, so können endliche Änderungen (Dx, Dy) verwendet werden:         


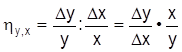
In diesem Fall spricht man von Bogen-E. Der Grenzwert der Bogen-E. (Dx ®:0) wird als Punkt-E. bezeichnet und gilt nur für einen bestimmten Punkt der Funktion :         


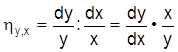
Für Funktionen mit mehreren unabhängigen (erklärenden) Variablen (y = f(x1,...,xn)) können zur Verdeutlichung der spezifischen Einflußstärken einer Größe partielle E. gebildet werden:         


        


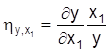
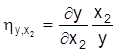
, usw.         


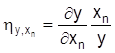
Die Summe aller partiellen E. der erklärenden Variablen wird auch als totale E. bezeichnet. Aus der Vielzahl der möglichen Funktionstypen sollen zwei für die Ökonomie besonders häufig angenommene Zusammenhänge herausgegriffen werden: lineare und isoelastische Funktionen. Lineare Funktionen haben eine konstante erste Ableitung (dy/dx = konstant), woraus aber nicht geschlossen werden kann, daß die E. entlang der Geraden ebenfalls konstant sind, da sich die Ausgangsgrößen x und y ändern können. Allgemein werden in diesen Fällen fünf Abschnitte der linearen Funktion identifiziert: ein vollkommen unelastischer Bereich h = 0, ein unelastischer Bereich  , ein elastischer Bereich h < |1| , ein vollkommen elastischer Bereich h = |¥| sowie den Bereich h = |1|. Nimmt man eine lineare Funktion mit negativer Steigung an, so lassen sich die Bereiche wie folgt zuordnen: Der Ort hy,x = -1 bezeichnet den Halbierungspunkt der Kurve und für hy,x  ist x = 0  sowie für hy,x = 0 gilt y =
0. In vielen Fällen kann es zur Vereinfachung der ökonomischen Analyse zweckmäßig sein, isoelastische Funktionen anzunehmen; sie zeichnen sich dadurch aus, daß die E. entlang der Kurve konstant bleiben. Diese Eigenschaft wird von Potenzfunktionen erfüllt: y = axb, mit a, b = konstant, da die E.         


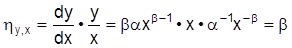
beträgt und somit bei einem konstanten Exponenten von den Ausprägungen von x und y unabhängig ist. Da jede E. als Steigung der logarithmierten Funktion ausgedrückt werden kann, läßt sich dieses Ergebnis auch unmittelbar aus log y = log a + b log x ableiten:          


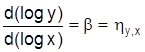
Liegt für eine isoelastische Funktion eine E. von 1 vor, so kann der Kurvenverlauf durch eine gleichseitige Hyperbel verdeutlicht werden. Aus der Vielzahl von E.-Definitionen sollen beispielhaft einige der am häufigsten verwendeten herausgegriffen werden. Die Preis-E. oder Eigenpreis-E. der Nachfrage hqd,pgib die Stärke der Nachfragemengenänderungen bei Preisänderungen des betreffenden Gutes an


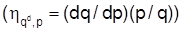
 . Für normal negativ geneigte Nachfragefunktionen  bei sinkendem Preis wird mehr nachgefragt und umgekehrt  ist diese E. negativ definiert. Je größer der absolute Wert der Preis-E., je elastischer die Nachfrage ist, um so eher sind die Nachfrager bereit, bei Preissteigerungen auf das Gut zu verzichten. Je unelastischer die Nachfrage hinsichtlich des Preises ist, um so unabweisbarer ist das Bedürfnis und um so kleiner ist der absolute Wert von hqd,p. I. Ggs. zur direkten Preis-E. beziehen sich die relativen Nachfragemengenänderungen der Kreuzpreis-E. der Nachfrage nicht auf den zugehörigen Gutspreis, sondern auf die Preisänderungen eines beliebigen anderen Gutes:         


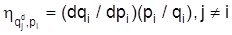
. Ist die Kreuzpreis-E. positiv, so bestehen zwischen den Güter i und j substitutive Beziehungen; für negative Kreuzpreis-E. kann auf komplementäre Güter (Gut) oder aber auf substitutive Güter (Gut) geschlossen werden, wobei im letzten Fall der Substitutionseffekt durch den Einkommenseffekt überkompensiert wird. Für sehr viele Güter, die in keiner Beziehung zueinander stehen, kann eine Kreuzpreis-E. von Null angenommen werden. Die Einkommens-E. der Nachfrage


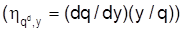
bildet den Zusammenhang zwischen der relativen Nachfrage- und inkommensveränderung ab. Die überwiegende Anzahl der Güter wird mit zunehmenden Einkommen auch vermehrt nachgefragt, so daß die Einkommens-E. positiv ist (superiore Güter). Ist sie negativ, so liegen inferiore Güter (Gut) vor. Umfassender als mit der Kreuzpreiselastizität der Nachfrage können die Konkurrenzbeziehungen zwischen Gütern durch die Substitutions-E.         


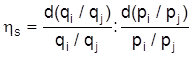
beschrieben werden, die die relativen Veränderungen der Mengenquotienten zu den relativen Variationen der relativen Preise zueinander in Beziehung setzt. Somit werden simultan die Änderungen aller betroffenen Mengen und Preise erfaßt. Da mit steigendem Marktpreis von den Unternehmen (Betrieb , I.) eine zunehmende Gütermenge angeboten wird, ist die direkte Preis-E. oder Eigenpreis-E. des Angebotes positiv


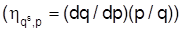
 , die zugehörigen Kreuzpreis-E. von Mehrproduktunternehmen sind bei Kuppelprodukten positiv und bei Gütern, die um dieselben begrenzten Inputfaktoren konkurrieren (Alternativproduktion) negativ. Letztlich ist die Ausprägung der Angebots-E. von der zugrundeliegenden Produktionstechnologie abhängig. Die im Zusammenhang damit am häufigsten verwendeten E. sind die partiellen und totalen Produktions-E., wobei die letztere auch als Niveau-E. oder Skalen-Elastizitäten auftreten kann. Die partielle Produktions-E. gibt an, wie groß die relative Outputveränderung bei einer relativen Veränderung eines Inputfaktors vi ist. Nach den Überlegungen zu Potenzfunktionen wird unmittelbar deutlich, daß die Exponenten mi einer Cobb-Douglas-Produktionsfunktion         


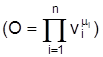
die partiellen Produktions-E. des zugehörigen Faktors vi darstellen. Die Summe aller partiellen Produktions-E. bildet die totale Produktions-E., die im Falle einer Cobb-Douglas-Funktion            


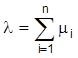
 beträgt.

Literatur: W. Krelle, Elastizitäten von Angebot und Nachfrage. HdSW, Bd.
3. Göttingen, Stuttgart, Tübingen 1961, 176-183. H. Gerfin/P. Heimann, Elastizität. HdWW, Bd.
2. Göttingen, Stuttgart, Tübingen 1980.