Miller-Orr-Modell

  stochastisches Kassenhaltungsmodell (1966), wobei das Problem der optimalen Überführung von überschüssigen Kassenbeständen (Kasse) in rentable kurzfristige Anlagen und nicht so sehr das komplexe Problem der Liquiditätssicherung (Liquidität) im Vordergrund steht. Dem Modell liegt innerhalb der Periode schwankender Kassenbestand zugrunde: Der Kassenbestand bewege sich innerhalb einer Periode in Richtung und Größe zufallsabhängig, jedoch könne über eine zunehmende Anzahl von Perioden eine Normalverteilung unterstellt werden. Der Planungszeitraum wird in gleich große Zeiteinheiten t unterteilt. In jeder Teilperiode wird ein Geldzufluß mit derWahrscheinlichkeit p und ein Geldabfluß mit der Wahrscheinlichkeit q erwartet. Zur Vereinfachung gilt p = q = 0,5. Transaktionskosten (Kosten) b fallen unabhängig von der Höhe und Richtung des Transfers an. Die angelegten Beträge erbringen einen Zins i. Innerhalb der Kontrollgrenzen null (Untergrenze) und h (Obergrenze) bewegt sich der Kassenstand frei. Erreicht er h, so wird der Kassenbestand auf das niedrigere Niveau z abgesenkt. Der Betrag (h-z) wird in eine kurzfristige Geldanlage übergeführt. Umgekehrt: Sinkt der Kassenbestand auf null, wird ein Betrag in Höhe von z aus der Geldanlage entnommen und der Kasse zugeführt. Das Modell bestimmt unter Maximierung der Rentabilität das Optimum von h und z:            


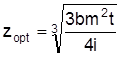
            hopt = 3zopt