Zeitreihenanalyse

umfaßt die Gesamtheit der Methoden zur Untersuchung von Zeitreihen (ZR), d.h. von Folgen zeitlich angeordneter numerischer Beobachtungen jeweils eines bestimmten Sachverhaltes. Das erste Ziel bei der Analyse einer ZR besteht im Erkennen von Gesetzmäßigkeiten im zeitlichen Verlauf. Diese sind i.d.R. nicht exakt durch mathematische Funktionen erfaßbar. Daher sieht man die einzelnen Werte als zufällig gestört, d.h. als Realisationen von Zufallsvariablen an. Die Z. wird damit zu einem Spezialgebiet der Statistik. Hervorstechende Gesetzmäßigkeiten in vielen ökonomischen ZR sind:         
(1)        Die Trendkomponente, d.i. die langfristige Entwicklung des mittleren Niveaus einer ZR.         
(2)        Die Konjunkturkomponente; sie stellt eine mehrjährige, nicht notwendig regelmäßige Schwankung dar.         
(3)        Die Saisonkomponente; diese ist eine jahreszeitlich bedingte Schwankung, die sich jedes Jahr wiederholt und sich höchstens langsam ändert. Dabei werden
(1) und
(2) bisweilen zur glatten,
(2) und
(3) alternativ zur zyklischen Komponente zusammengefaßt. In der Restkomponente, die nach der Elimination der obigen systematischen Komponenten aus der ZR übrig bleibt, sind i.d.R. weitere Gesetzmäßigkeiten enthalten, und zwar in Form von Abhängigkeiten der jweils gleichweit auseinander liegenden Beobachtungen. Die Erfassung der Abhängigkeiten als Funktion des Abstandes oder Zeit-Lags geschieht mittels geeignet modifizierter Korrelationskoeffizienten (Regressionsanalyse). Die (Auto-) Korrelationsfunktion ist dann die Basis der weitergehenden Verfahren der ZRA. Für weitergehende Betrachtungen sind stochastische Modelle für ZR unabdingbar. Modelle beschreiben dabei nicht notwendig den wahren Erzeugermechanismus, sondern einen möglichst einfachen Mechanismus, der Reihen von ähnlicher Gestalt hervorbringt. Das klassische Komponentenmodell zerlegt eine ZR


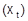
 additiv oder multiplikativ in die oben genannten Komponenten:


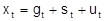
  bzw. 


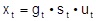
  , wobei (gt) den Trend oder die glatte Komponente,  (st) die Saison- und (ut)  die Restkomponente darstellt. Für die Saisonbereinigung, d.h. die Schätzung und Elimination der saisonalen Komponente, sind komplizierte und rechenaufwendige Verfahren entwickelt worden. Zu nennen sind insbesondere das Census X 11-, das ASA II- und das Berliner Verfahren. Die Schätzung von (gt) erfolgt in diesem Rahmen meist durch die Anwendung gleitender Durchschnitte oder über die Anpassung von einfachen Zeitfunktionen. Die neueren Modelle gehen von schwach stationären stochastischen Prozessen aus. Dies sind Folgen von Zufallsvariablen (Xt) bei denen sich Erwartungswert ,    Varianz und Abhängigkeitsstruktur über die Zeit nicht ändert. Diese Prozesse bilden auch den theoretischen Hintergrund für die Spektralanalyse . Hier geht man davon aus, daß ZR aus zyklischen Bestandteilen aller möglichen Perioden zusammengesetzt sind. Eine Transformation der Autokorrelationsfunktion erlaubt hierbei zu erkennen, mit welcher Stärke Zyklen in der Reihe vertreten sind. In der empirischen Analyse erscheint der Trend dann als Zyklus mit sehr großer Periode und die Saison als zyklische Schwankung mit der Saisonperiode. Konjunkturzyklen (Konjunkturtheorie) wirken sich nur bei selten vorliegenden, sehr langen Reihen aus. Besondere Bedeutung haben in den siebziger Jahren die ARIMA - Prozesse , auch Box-Jenkins-Modelle genannt, erhalten. Die Zufallsvariablen Xt werden dabei als gewichtete Summe von vergangenen beobachteten Werten und von Störungen angesehen. Die Modellgleichung eines stationären ARMA-Prozesses lautet:              


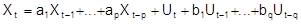
Bei Reihen mit Trend bzw. Saison benötigt man instationäre Modelle. Box und Jenkins bilden aus diesem Grund geeignete Differenzen und sehen erst die transformierte ZR als Realisation eines ARMA-Prozesses an. Das Modell für die Ausgangsreihe wird dann als ARIMA-Prozeß bezeichnet. Die Bedeutung der Box-Jenkins-Modelle liegt darin, daß zwar nur wenige Parameter bestimmt werden müssen, sie aber dennoch flexibel genug sind, eine Vielzahl von empirischen ZR hinreichend genau zu beschreiben. Ein großes Defizit weisen sie aber bzgl. der Interpretierbarkeit der angepaßten Modelle auf. Auch aus diesem Grund ist seit einiger Zeit eine erneute Hinwendung zu strukturellen Modellen zu beobachten. Diese werden nunmehr im Rahmen von Zustandsraum-Modellen betrachtet. Zustandsraum-Modelle sind durch zwei Gleichungen gegeben. Die Systemgleichung beschreibt die (stochastische) Entwicklung des Zustandes, i.d.R. der strukturellen Komponenten. Mit der Beobachtungsgleichung wird erfaßt, daß der Zustand nicht direkt beobachtet wird, sondern transformiert und durch Zufallsstörungen überlagert. Ein wichtiges Anwendungsgebiet der Z. ist die Prognose . Hier geht es um die Extrapolation der vorliegenden ZR in die Zukunft. Regressionsansätze beim klassischen Komponentenmodell haben sich nicht bewährt. Favorisiert werden vielmehr einerseits die einfachen, aber heuristischen Methoden des exponentiellen Glättens und andererseits die auf ARIMA-Modellen basierenden Box-Jenkins Prognosen. Bei den ARIMA-Modellen erhält man die Prognose durch sukzessives Fortschreiben der Definitionsgleichung, wobei zukünftige Störungen außer acht gelassen werden. Diese beiden Prognoseverfahren können als Spezialfälle des Kalman-Filters aufgefaßt werden, der ein rekursives, prognoseorientiertes Verfahren zur Schätzung von Zustandsraum-Modellen darstellt. Bis jetzt wurde von univariaten ZR ausgegangen; die Beobachtungen sind einzelne Zahlen. Bestehen sie jeweils aus Wertepaaren oder mehreren Werten, so liegt eine bi- bzw. multivariate ZR vor. Diese kann auch als gleichzeitige Beobachtung mehrerer univariater ZR aufgefaßt werden. Bei multivariaten ZR sind die Abhängigkeiten zwischen den einzelnen univariaten ZR, aus denen sie sich zusammensetzen, von zentraler Bedeutung. Sie werden mit den Kreuzkorrelationsfunktionen erfaßt. Das darauf basierende Kreuzspektrum gibt in zweierlei Hinsicht Aufschluß über die Abhängigkeiten zwischen zwei ZR, und zwar über die Korrelationen zwischen den Zyklen gleicher Periode und über die Phasenverschiebung der zyklischen Bestandteile der ZR. Die modellmäßige Erfassung der Beziehungen zwischen zwei ZR geschieht größtenteils im Rahmen linearer Systeme. Die ZR (yt) hängt z.B. linear von der ZR (xr)ab, wenn 


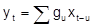
 mit festen Gewichten  gu gilt. Derartige Transformationen werden auch als Filtration bezeichnet. In der Praxis interessiert vor allem, ob eine Beziehung dieser Art existiert, wie sie ggfs. aussieht und ob (xt) zu einer Verbesserung der Prognose von (yt) beiträgt. Die Z. zählt zu den am intensivsten beforschten Gebieten der Statistik. Nachdem die Untersuchung der ARIMA-Modelle als weitgehend abgeschlossen angesehen werden kann, sind heutzutage noch verschiedene Verallgemeinerungen von Interesse. Immer mehr Gewicht gewinnt wie angedeutet der systemtheoretische Zugang. Einmal können mit ihm leicht Instationaritäten erfaßt werden. Diesen gilt derzeit ein relevanter Teil der Aufmerksamkeit. Zum anderen geben sie auch einen geeigneten Rahmen für nichtlineare Prozeß- Modelle, die einen Schwerpunkt der aktuellen Forschung bilden.

Literatur: G. E. P. Box/G. M. Jenkings, Time Series Analysis, Forecasting And Control. San Francisco 1976. A. C. Harvey, Forecasting, structural time series models and the Kalman filter. Cambridge 1989. M. B. Priestley, Spectral Analysis And Time Series, Vol. 1: Univariate Series, Vol. 2: Multivariate Series, Prediction And Control; London 1981. R. Schlittgen/B. H. J. Streitberg, Zeitreihenanalyse. München 1984.