Regressionsanalyse

Die Regressionsanalyse ist ein häufig eingesetztes Analyseverfahren (Datenanalyse), das sowohl für die Beschreibung und Erklärung von Zusammenhängen als auch für die Durchführung von Prognosen grosse Bedeutung besitzt. Untersucht werden die Wirkungsbeziehungen zwischen einer abhängigen Va­riablen (Regressand) und einer oder mehreren unabhängigen Variablen (Regressoren). Die Regressi­onsanalyse ist anwendbar, wenn sowohl die abhängige als auch die unabhängige Variablen metrisches Skalenniveau (Messniveau) besitzen. Ein Beispiel für die Anwendung der Regressionsanalyse bildet die Frage, ob und wie die Absatzmenge eines Produktes vom Preis (und ggf. zusätzlich von den Werbeausgaben und der Zahl der Verkaufsstät­ten) abhängt. Nach der Anzahl der einbezogenen Variablen wird zwischen der einfachen (zwei Variab­len) und der multiplen Regressionsanalyse (mehr als zwei Variablen) unterschieden. Ferner wird nach der Art der Zusammenhänge zwischen linearer und nicht-linearer Regressionsanalyse differenziert.

Die Regressionsanalyse untersucht die lineare Abhängigkeit zwi­schen einer metrisch skalierten abhängigen Variablen (Regressand) und einer oder meh­reren (Regressionsanalyse, multiple) me­trisch skalierten unabhängigen Variablen (Regressoren). Der Zwei-Variablen-Fall bil­det die einfachste stochastische Beziehung zwischen zwei Variablen x und y ab mit dem Modell oder für die Stichprobe y ist hier die abhängige Variable, x die unab­hängige oder erklärende Variable, £ eine sto­chastische Störgröße und ßo und ßi die unbe­kannten Regressionsparameter, bo, bi, e; die geschätzten Parameter. Das Subskript i be­zeichnet die i-te Beobachtung. Die Werte für x und y sind beobachtbar, die für e nicht. Beobachtungen können über die Zeit (Zeitreihenanalyse), über Personen bzw. Objekte (Querschnittsanalyse) oder glei­chermaßen über Zeit und Personen vorlie­gen. Aufgrund der stochastischen Eigen­schaft des Modells durch die Störgröße e existiert für jeden der Werte von x auch eine Wahrscheinlichkeitsverteilung für die Werte von y. Dem Regressionsmodell liegen fünf Annah­men über die Eigenschaft der Störgrößen zu­grunde: Ei ist normalverteilt. & hat einen Erwartungswert von Null: E (£i) = 0- . , Jedes Residuum hat die gleiche Varianz er (Homoskedastizität): E (£;2) = CT2 für alle i. Die Residuen sind nicht autoregressiv, d.h. sie sind paarweise unkorreliert: E (£i£j) = 0,i*j. Die erklärende Variable x; ist nicht stocha­stisch und hat bei Meßwiederholungen fe­ste Werte. Das Regressionsproblem besteht darin, Schätzwerte für ßi und £ zu finden. Die Schät­zung der Regressionsparameter kann über die Kleinste-Quadrate-Schätzung erfol­gen. Durch die Punkte der Beobacntungs- werte (x, y) wird dabei eine Gerade gelegt, so dass die Summe der quadrierten Abweichun­gen (Residuen) minimiert wird. Sind die An­nahmen des Modells erfüllt, dann sind nach dem Gauss-Markov- Theorem die geschätz­ten Koeffizienten b beste lineare erwartungs­treue Schätzer (BLUE) für die gesuchten Parameter. Aus der Gleichung des linearen Regressionsmodells ergibt sich die Zielfunk­tion für die Schätzung
Nach der Methode der Kleinsten Quadrate ergeben sich die Parameter aus: wenn bi festgelegt ist. Unter den Annahmen des klassischen linearen Regressionsmodells sind die Kleinste-Quadrate-Schätzung und die Maximum Likelihood Schätzung äquivalent. Durch die Annahme normalverteilter Resi­duen besteht die Möglichkeit Hypothesen über den Einfluß des Regressors zu testen. Soll der Einfluß als statistisch gesichert ange­sehen werden, so ist die Nullhypothese Ho: ß = 0 gegen die Alternativhypothese Hi : ß  0 zu prüfen. Sind die Annahmen des Re­gressionsmodells erfüllt, dann ergibt sich für die Nullhypothese die Teststatistik über t = b/Sb- Die Prüfgröße folgt einer t-Vertei­lung mit (n-2) Freiheitsgraden. Ist der empi­rische t-Wert gleich oder größer als der kriti­sche Tabellenwert ta/2, bei vorgegebenem Signifikanzniveau a, dann ist statistisch gesi­chert, dass der Regressionskoeffizient von 0 verschieden ist. Die Güte des Regressionsmodells wird über das Bestimmtheitsmaß (Determinationsko­effizienten) R2 gemessen. Er erfaßt den An­teil der Varianz in y, der auf die Varianz von x zurückzuführen ist. Das Bestimmtheitsmaß des einfachen Regressionsmodells ist defi­niert über R2 hat einen Wertebereich zwischen 0 und 1. Ein Wert von 0 gibt den schlechtesten Fit, der Wert 1 den besten Fit an. Die Probleme des einfachen Regressionsmodells entstehen bei Verletzung der Modellannahmen wie: Nichtlinearität, Autoregressiven Residu­en (Autokorrelation), Heteroskedastizität. Das Modell eignet sich sowohl zur Prognose als auch zur Diagnose von Beziehungen und ist in fast allen statistischen Datenanalyseprogrammenenthalten.

Siehe auch Regression,

Literatur:  Kmenta, Elements of Econometrics, New York 1986. Schneeweiß, H., Ökonometrie, Würzburg 1971.
Literatur: Backhaus K., Erichson B., Plinke W., Weiber R.: Multivariate Analysemethoden. Eine anwendungsorientierte Einführung, 10. Auflage, Springer, Berlin u.a., 2003.

faßt Verfahren zusammen, die sich mit der Untersuchung von Zusammenhängen, stochastischen Abhängigkeiten zwischen Variablen befassen, wobei i. Ggs. zur Korrelationsanalyse die betrachteten Größen unterschiedlich aufgefaßt und behandelt werden: Zu klären ist für eine Größe, welche Einflußfaktoren auf sie einwirken und welcher Art dieser Einfluß ist. Folgendes einfache Beispiel verdeutlicht die anstehende Fragestellung: Es bezeichne C die Konsumausgaben eines Haushalts und Y das verfügbare Einkommen . Man wird erwarten, daß die Konsumausgaben wesentlich vom verfügbaren Einkommen abhängen. Trifft diese Erwartung in voller Strenge zu, so liegt ein funktionaler Zusammenhang der Gestalt
(1)  C = g(Y) vor, wobei die Funktion g i.a. nicht bekannt ist. Zur Klärung der genannten Fragen geht man so vor, daß man für die als relevant erachteten Größen Beobachtungen sammelt. Im Beispiel erhält man so etwa T Datensätze (C1, Y1), ..., (CT, YT), u. zw. in Form von Zeitreihendaten oder Querschnittsdaten oder in Form einer Mischung dieser Datentypen. Die Auswertung zeigt dann in aller Regel, daß ein strenger funktionaler Zusammenhang der Art
(1) nicht besteht. Zwar kann man leicht Funktionen g mit der Eigenschaft
(2)  Ct = g(Yt)  ,t = 1, ..., T, ermitteln, jedoch trifft
(2) nicht für alle möglichen Wertepaare (Y¢, C¢) zu, wie es die Beziehung
(1) verlangt. Auch bei Berücksichtigung weiterer Einflußgrößen ergibt sich  abgesehen von Extremfällen  die gleiche Situation wie zuvor, daß nämlich ein strenger funktionaler Zusammenhang nicht unterstellt werden kann. Dies läßt sich dadurch erklären, daß neben den explizit berücksichtigten Größen, denen eine systematische Wirkung auf die Konsumausgaben zukommt, noch weitere Einflußfaktoren vorhanden sind. Diese üben zwar einzeln keine erkennbare, systematische Wirkung aus, sie überlagern sich jedoch und bewirken insgesamt irreguläre Abweichungen von einem strengen funktionalen Zusammenhang. Solche Abweichungen sind hier auch insofern zu erwarten, als im Beispiel menschliches Verhalten erfaßt werden soll, also Verhaltensweisen, die nicht allein durch rationale Überlegungen bestimmt sind. Entsprechend dieser Deutung, die natürlich nicht nur für das Beispiel gültig ist, geht man von folgendem Konzept zur Erfassung des interessierenden Zusammenhangs aus: Man setzt die zu klärende Größe als Funktion der als wesentlich erachteten Einflußfaktoren zuzüglich einer additiven zufälligen Störgröße an. Man erhält also den Ansatz
(3)  y = g (x1,..., xn) + u , darin bezeichnet y die zu erklärende Größe, x1, ..., xn die systematischen Einflußfaktoren von y, u die zufällige Störgröße. In dieser Aufspaltung nennt man die systematische Komponente g (x1, ..., xn) Regressionsfunktion und die irreguläre Komponente u latente (Stör-) Variable  da u nach Annahme nicht beobachtet werden kann. Ziel der R. ist die Ermittlung der Regressionsfunktion im Sinne einer Schätzung, die als Näherung für die nicht bekannte Regressionsfunktion brauchbar ist. Denn die Bestimmung der wahren Funktion ist nicht möglich. Die Schätzung erfolgt im Rahmen eines Modells , d.h. es ist ein Satz von Annahmen zu formulieren, die
(3) dann auch erst zu einem sinnvollen, identifizierbaren Ansatz machen. Im klassischen multiplen linearen Regressionsmodell (auch: Modell der linearen Mehrfachregression) unterstellt man für die Regressionsfunktion die mathematisch einfachste Gestalt, nämlich eine lineare Funktion. Das Modell hat folgendes Aussehen (der Zählindex für die Beobachtungen wird der Einfachheit halber als Zeitindex interpretiert): Zwischen den Größen y, x1, ..., xn, u besteht ein linearer Zusammenhang, der zu den Zeitpunkten t = 1, ..., T beobachtet werden kann, es gilt: (A1)   Yt = b0 + b1xt1 + ... + bnxtn + ut ,     t = 1, ... T.                       (A2)  Die Beobachtungen xtk, t = 1, ..., T, k = 1, ..., n sind exogen bestimmte,       deterministische Größen. (A3)  Der Rang der Beobachtungsmatrix                                    


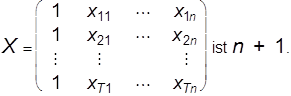
(A4)  E (ut) = 0, t = 1, ..., T, Var (ut) = s2, t =1,...,T (Homoskedastie),          cov (ut, ut\') = 0 für t  ¹  t¢ (keine Autokorrelation). (A5)  u1, ..., uT sind normal verteilt. Bezeichnungen: yt:  endogene /abhängige/ zu erklärende Variable, Regressand xtk:            exogene/praedeterminierte/erklärende Variable, Regressoren ut:  Stör-, Rest-, latente Variable bo: Absolutglied (nicht bekannte reelle Zahl) b1, ..., bn:  Regressionskoeffizienten (nicht bekannte reelle Zahlen). Die Annahmen stellen Restriktionen von unterschiedlicher Stärke dar. So ist die Annahme eines linearen Zusammenhanges sehr restriktiv, bei Anwendungen ist zu prüfen, ob die Annahme jedenfalls als Näherung brauchbar oder evtl. durch eine Variablentransformation erreichbar ist. Die Annahme (A2) bedeutet ebenfalls eine gewichtige Einschränkung, sie ist beispielsweise verletzt, wenn als Regressoren auch verzögerte Variablen des Regressanden herangezogen werden. Unterstellt man im Eingangsbeispiel die sog. Habit-Persistence-Hypothese , so erhält man im linearen Fall      Ct = b0 + b1 Yt + b2 Ct-1 + ut, t = 1, ..., T, und (A2) gilt nicht. Die Rangbedingung (A3) besagt anschaulich, daß die Beobachtungen der Regressoren genügend breit variieren müssen. Im Fall der einfachen linearen Regression (n = 1) dürfen z.B. nicht alle Werte xt1 übereinstimmen. Bei Anwendungen können Schwierigkeiten auftreten, wenn (A3) zwar erfüllt ist, die Beobachtungen jedoch starke Bindungen aufweisen (Problem der Multikollinearität). Die Annahmen (A4) und (A5) kennzeichnen die stochastischen Eigenschaften des Modells. Sie sind für die nicht beobachtbaren Störvariablen formuliert, mittels der Regressionsbeziehung (A1) können sie jedoch auch als Forderungen an die beobachtbaren, abhängigen Variablen yt dargestellt werden. Die Forderungen in (A4) über die Existenz und das Aussehen von Erwartungswerten, Varianzen und Kovarianzen der Störvariablen werden zur Analyse der Eigenschaften der Modellschätzung benötigt, während die Normalverteilungsannahme (A5) zur Konstruktion von Tests und Bereichsschätzungen (induktive Statistik) dient. Unter den Annahmen sind die Homoskedastie (Gleichheit der Varianzen) und die Unkorreliertheit der Störvariablen bei Anwendungen als problematisch zu beurteilen und bedürfen der Kontrolle. Für die Schätzung der nicht bekannten Regressionskoeffizienten und der Varianz der Störvariablen wird im klassischen Modell zumeist die sog. Kleinst-Quadrate-Methode (kurz: KQ-Methode) verwendet, dieser liegt die folgende Idee zugrunde: Man bestimme die Regressionsfunktion g so, daß die Summe D der quadrierten Abstände der Beobachtungspunkte (xt1, ..., xtn, yt) von den zugehörigen Punkten (xt1, ..., xtn, g (xt1, ..., xtn)) minimal wird. Im linearen Fall hat man demnach die Funktion    
(4)       


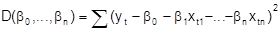
zu minimieren. Zur Lösung dieser Minimierungsaufgabe setzt man die ersten partiellen Ableitungen von D gleich Null:
(5)    


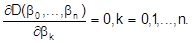
Das resultierende Gleichungssystem ist linear in den bk und kann umformuliert werden zu den sog. Normalgleichungen
(6)         


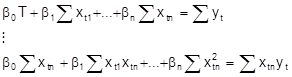
Wg. (A3) besitzt dieses Gleichungssystem genau eine Lösung


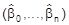
, dies ist die gesuchte Minimalstelle von D. Man nennt


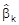
 den KQ-Schätzer für bk,  k = 0, ..., n. Im Fall der einfachen linearen Regression (n = 1) erhält man die KQ-Schätzer
(7)            


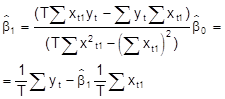
Eine formelmäßige Darstellung der


 ist für größere n nur noch in Matrixdarstellung übersichtlich. Mittels der KQ-Schätzer ergeben sich als Schätzung für die Regressionsfunktion
(8)       


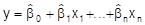
und durch Einsetzen der xtk in
(8) die geschätzten Regressionswerte


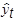
. Die Differenz zwischen einem beobachteten und dem geschätzten Wert bezeichnet man als Residuum:
(9)    


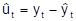
, t = 1, ..., T. Die Residuen lassen sich als Schätzung für die nicht beobachtbaren Störvariablen auffassen, durch (10)  


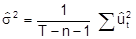
ist ein erwartungstreuer Schätzer (induktive Statistik) für s2 gegeben. Die Benutzung der KQ-Schätzung rechtfertigt sich mit ihren Optimalitätseigenschaften. Zur Beurteilung etwa des Schätzers für den Regressionskoeffizienten bk betrachtet man den Schätzfehler 


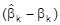
 sowie den quadratischen Schätzfehler


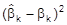
. Der KQ-Schätzer


 ist erwartungstreu, d.h. E


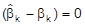
 , k = 0, ..., n. Der KQ-Schätzer


 ist linear in den yt, und das Gauß-Markoff-Theorem besagt, daß er unter allen linearen, erwartungstreuen Schätzern für bk den kleinsten mittleren quadratischen Fehler besitzt, d.h. es ist


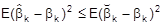
  für jeden Schätzer


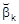
 des genannten Typs; ist obendrein die Normalverteilungsannahme (A5) erfüllt, so kann die Beschränkung auf lineare Schätzer fallengelassen werden. Mittels statistischer Tests können Hypothesen über die Regressionskoeffizienten geprüft werden. Routinemäßig prüft man z.B. die Hypothesen H0 : bk = 0 (keine Abhängigkeit vom k-ten Regressor) gegen H1 : bk ¹ 0, aber auch z.B. H0 : b0 = ... = bn = 0 (die Regressoren besitzen keinen Erklärungswert) gegen H1 : H0 falsch. Ebenso können Hypothesen über lineare Zusammenhänge zwischen den Koeffizienten oder über Änderungen der Koeffizienten im Beobachtungszeitraum (Test auf Strukturbruch) geprüft werden. Die dazu verwendeten Tests besitzen alle die Eigenschaft, daß eine irrtümliche Ablehnung der Nullhypothese H0 höchstens mit einer vorgegebenen Wahrscheinlichkeit a, dem sog. Signifikanzniveau , erfolgt. Für kleinere Werte von a, üblich sind z.B. a =
0. 05, a =
0. 01 o.ä., spricht man bei einer Ablehnung von H0 von einem signifikanten Gegensatz zwischen Beobachtungen und Nullhypothese, z.B. bei Ablehnung von H0 : bk = 0 wird bk als signifikant verschieden von Null bezeichnet. Im Hinblick auf Anwendungen ist das klassische lineare multiple Regressionsmodell insofern attraktiv, als die Schätzung relativ leicht zu bewerkstelligen ist und die Schätzer wünschenswerte Eigenschaften besitzen. Falls jedoch ernstere Zweifel an seiner Anwendbarkeit bestehen, müssen Erweiterungen des Modells betrachtet werden. Dies ist insbesondere der Fall, wenn zur Erklärung einer abhängigen Variablen neben unabhängigen Größen weitere Variablen herangezogen werden müssen, die untereinander Abhängigkeiten aufweisen (Situationen dieser Art treten bereits bei einfachen Marktgleichgewichtsmodellen (Gleichgewicht) in Form einer Angebots-, einer Nachfragefunktion nebst einer Gleichgewichtsbedingung auf). Statt einer sind zugleich mehrere abhängige Variable zu betrachten, statt einer Gleichung hat man zu jedem Zeitpunkt mehrere Gleichungen zu betrachten. Man bezeichnet diese Ansätze als Mehrgleichungsmodelle oder auch als interdependente Systeme. Die relevanten ökonometrischen Modelle, die seit den späten dreißiger Jahren für viele Staaten und Wirtschaftsregionen aufgebaut wurden, sind von diesem Typ.

Literatur: P. J. Dhrymes, Introductory Econometrics. New York, Heidelberg, Berlin 1978. H. Schneeweiß. Ökonometrie. Würzburg, Wien 1990. A. Sen/M. Srivastava, Regression Analysis. Theory, Methods and Applications. New York, Heidelberg, Berlin 1990.