|
Korrelationsanalyse
Verfahren zur Messung von Wechselbeziehungen (Korrelation) zwischen sich verändernden Größen. Je nach Anzahl der untersuchten Variablen unterscheidet man zwischen einfacher (zwei Variablen) und der multiplen Korrelationsanalyse (mehrere Variablen). Als Maß für die Stärke und Richtung des Zusammenhangs dient dtr Korrelationskoeffizient, der den Wert 0 einnimmt, falls die Variablen linear unabhängig bzw. unkorreliert sind. Die Variablen sind umso stärker korreliert, je näher der Wert bei ± 1 liegt. Der lineare Korrelationskoeffizient (nach Bravais-Pearson) für metrische Variablen zwischen zwei Variablen ist definiert als
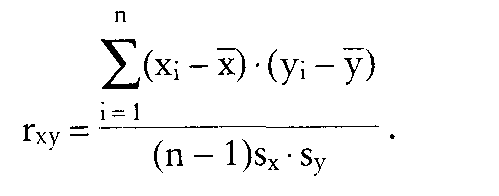
sx und sy stehen für die Standardabweichungen, x und y für die Mittelwerte der Variablenrealisationen x; und yi. Korrelationskoeffizienten, die auf nichtmetrischen Daten beruhen, aber ähnliche Eigenschaften wie rxy haben, sind der Te- trachorische, Polychorische und Polyserielle Korrelationskoeffizient (mit der Annahme kontinuierlicher normalverteilter Variablen aber kategorieller Messung).
Die K. beschäftigt sich mit der quantitativen Bestimmung der Stärke des linearen Zusammenhangs von Merkmalen oder Variablen . Hierzu werden Maßzahlen (Korrelationen), die Werte im Intervall von 1 bis +1 annehmen, verwandt. Beim Wert +1 spricht man von einem (totalen) positiv linearen, beim Wert 1 von einem (totalen) negativ linearen Zusammenhang und der Wert 0 besagt, daß kein linearer (eventuell aber doch z.B. ein quadratischer) Zusammenhang zwischen den Variablen besteht, d.h. die Variablen sind unkorreliert. Je weiter eine Korrelation vom Wert 0 abweicht, desto stärker ist natürlich der lineare Zusammenhang der Merkmale. Die Korrelation zwischen zwei Merkmalen X und Y, die in einem sachlogischen Zusammenhang stehen sollten, da sonst sogenannte Nonsenskorrelationen entstehen, schätzt man durch einen Korrelationskoeffizienten. Dazu werden an n Objekten aus einer interessierenden Grundgesamtheit die beiden Merkmale X und Y beobachtet, so daß dann n Beobachtungs-Tupel (x1, y1), (x2, y2), ..., (xn, yn) zur Verfügung stehen. Bezeichnen
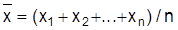
und
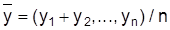
die arithmetischen Mittel der n Beobachtungswerte für die Merkmale X und Y, so ist der für metrische (in der Gesamtheit normalverteilte) Merkmale (Deskriptive Statistik) übliche Pearsonsche Korrelationskoeffizient gegeben als
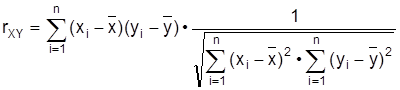
Um zu prüfen, ob der Zusammenhang zwischen X und Y signifikant ist, d. h., ob X und Y tatsächlich korreliert sind, oder ob ein Wert rXY ¹ 0 nur daher rührt, daß man lediglich n Objekte und nicht die Gesamtheit aller Objekte untersucht hat, kann man sich eines Korrelationstests bedienen. Und zwar verwirft man die Hypothese der Unkorreliertheit zum Sicherheitsniveau a Î (0, 1) , zumeist a =
0. 9, a =
0. 95 oder a =
0. 99, falls mit
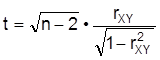
gilt
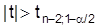
, wobei tn-2;g das g-Quantil der zentralen t-Verteilung mit n-2 Freiheitsgraden bezeichnet. Kann man von vornherein einen positiven (negativen) linearen Zusammenhang von X und Y ausschließen, so wird die Hypothese zum Niveau a verworfen, falls t < tn-2;a (t > tn-2;1-a). Sind die Merkmale X und Y nicht normalverteilt oder lediglich ordinaler Natur, so wird ihre Korrelation durch sogenannte Rangkorrelationskoeffizienten geschätzt. Dazu werden in den beiden Reihen x1, ..., Xn und y1, ..., yn getrennt Rangzahlen vergeben. Bezeichnet etwa x
(1) £ x
(2) £ ,..., £ x(n) die geordnete Beobachtungsreihe zum Merkmal X, so wird dem kleinsten Wert x
(1) die Rangzahl R (x
(1)) = 1, dem Wert x
(2) die Rangzahl R (x
(2)) = 2 dem größten Wert x(n) die Rangzahl R (x(n)) = n zugeordnet. Sind mehrere Beobachtungswerte gleich (Bindungen), so werden die in Frage stehenden Rangzahlen gemittelt (midranks) und der Mittelwert den jeweils gleichen Beobachtungswerten zugeordnet; genauso verfährt man mit y1, ..., yn. Dann ist etwa der Spearmansche Rangkorrelationskoeffizient als Maß für die Korrelation von X und Y gerade
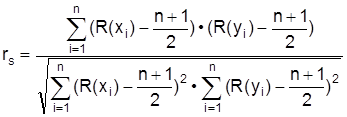
also der Pearsonsche Korrelationskoeffizient der Rangzahlen. Ein anderer Rangkorrelationskoeffizient ist Kendalls t. Bei ihm werden zunächst wie beim Spearmanschen Koeffizienten Rangzahlen vergeben. Sodann werden die ursprünglichen Beobachtungstupel (x1, y1), (x2, y2), ..., (xn, yn) nach der Größe der Rangzahlen zum Merkmal X geordnet; bei Bindungen wird die Reihenfolge zufällig festgelegt. Sodann zählt man für i=1, ..., n die Anzahl der Werte yj die in der Reihenfolge hinter yi stehen und kleiner oder gleich yi sind. Bezeichnet man die Anzahlen mit q1, ..., qn, so berechnet sich Kendalls t zu
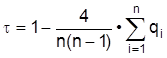
Weitere Korrelationskoeffizienten bzw. (bei nominalen Merkmalen) Assoziationsmaße, Korrelationstests und -konfidenzintervalle sowie Methoden zum Vergleich mehrerer Korrelationskoeffizienten findet man z.B. in Hartung et al. (1985, Kap. VII und IX) und Hartung/Elpelt (1986, Kap. III). Oft wird eine Korrelation zwischen zwei Merkmalen X und Y nur dadurch verursacht, daß beide Merkmale stark mit einem dritten Merkmal Z korreliert sind (Scheinkorrelation von X und Y). Um die eigentliche Korrelation der Merkmale X und Y messen zu können, muß man den Einfluß von Z ausschalten und partialisieren. Dies geschieht durch Verwendung partieller Korrelationskoeffizienten. Hier müssen an n Objekten alle drei Merkmale X, Y und Z beobachtet werden, wodurch die Tripel (x1, y1, z1), (x2, y2, z2), ..., (xn, yn, zn) zustandekommen. Basierend auf den Pearsonschen Korrelationskoeffizienten rXY, rXZ und rYZ zwischen je zweien der Merkmale wird die partielle Korrelation von X und Y unter Partialisierung von Z dann durch
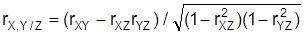
geschätzt. Basierend auf Kendalls t resp. auf den drei Rangkorrelationskoeffizienten tXY, tXZ, tYZ kann diese partielle Korrelation auch durch
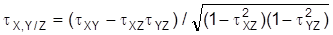
geschätzt werden. Für weitere Ausführungen zu partiellen Korrelationen, insbesondere diesbezügliche Korrelationstests sei verwiesen auf Hartung et al. (1985) und Hartung/Elpelt (1986). Als Maß für den linearen Zusammenhang einer Variablengruppe und eines einzelnen Merkmals dient die multiple Korrelation. Im einfachsten Fall besteht die Variablengruppe aus zwei Merkmalen X1 und X2, deren Zusammenhang mit einem dritten Merkmal Y untersucht werden soll. Wie im Fall partieller Korrelationen berechnet man zunächst anhand von n an Objekten einer interessierenden Grundgesamtheit beobachteten Tripeln zu den drei Merkmalen zunächst die Pearsonschen Korrelationskoeffizienten
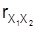
,
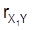
und
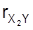
, um dann als Schätzer für die multiple Korrelation den multiplen Korrelationskoeffizienten
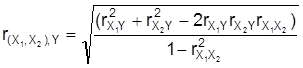
zu verwenden. Besteht die Variablengruppe aus drei Merkmalen X1, X2 und X3, so berechnet sich der multiple Korrelationskoeffizient als Schätzer für die multiple Korrelation zwischen der Gruppe (X1, X2 und X3) und dem Merkmal Y wie folgt. Durch Beobachtungen an n Objekten aus einer Grundgesamtheit beschafft man sich n Beobachtungs-Quadrupel zu den insgesamt vier Merkmalen und berechnet dann zunächst die Pearsonschen Korrelationskoeffizienten

,
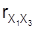
,
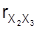
,

,

,
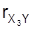
zwischen je zweien der vier Merkmale. Mit den Größen
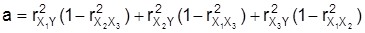
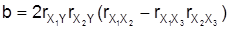
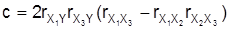
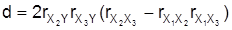
ergibt sich dann der multiple Korrelationskoeffizient zu
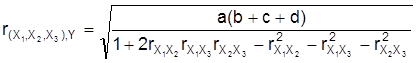
Der allgemeine Fall multipler Korrelationskoeffizienten sowie zugehörige Korrelationstests werden in Hartung/Elpelt (1986) behandelt. Für Korrelationen zwischen zwei Variablengruppen (kanonische Korrelationen) sowie (bi-) partielle multiple und kanonische Korrelationskoeffizienten und entsprechende Korrelationstests sei ebenfalls auf Hartung et al. (1985, Kap. IX) sowie Hartung/Elpelt (1986, Kap. III) verwiesen.
Literatur: J. Hartung/B. Elpelt/K.-H. Klösener, Statistik. Lehr- und Handbuch der angewandten Statistik. 10. A., München- Wien 1995. J. Hartung/B. Elpelt, Multivariate Statistik. Lehr- und Handbuch der angewandten Statistik. 5. A., München Wien 1995.
Literatur: Hammann, P.; Erichson, B., Marktforschung, 2. Aufl., Stuttgart 1990. Olsson, U.; Dras- goui, F.; Dorans, N.J., The polyserial correlation coefficient, in: Psychometrika, Vol. 47 (1982), S. 337-347.
|