Deskriptive Statistik

Die d. stellt Verfahren zur Verfügung, um Datenmaterial (Daten,
3.) zu ordnen, in Tabellen und Schaubildern übersichtlich darzustellen und um wesentliche Eigenschaften durch Kennwerte (Parameter) zu beschreiben. Diese Darstellungen oder Kennwerte können zunächst eng an die inhaltliche Bedeutung der Daten gebunden sein, was sich in vielen fachspezifischen Maßzahlen äußert (z.B. bei Preisindices, Indexzahl). Als methodische, nicht fachgebundene Wissenschaft analysiert und systematisiert die D. Verfahren der Datenaufbereitung, um tieferes Verständnis zu vermitteln, neue Anwendungsmöglichkeiten zu eröffnen oder Interpretationsmuster zu geben. Sie unterscheidet sich von der Induktiven Statistik, dem anderen Hauptgebiet der Statistik, dadurch, daß sie sich auf die Beschreibung der empirisch erhobenen Daten beschränkt und nicht versucht, Schlüsse von Stichproben auf Grundgesamtheiten zu begründen. Grundlegende Begriffe. Eine Erhebung soll die Untersuchungseinheiten unter bestimmten Gesichtspunkten klassifizieren oder untersuchen (z.B. die Einwohner eines Landes nach Alter, Geschlecht usw.). Ein derartiger Gesichtspunkt heißt Merkmal : die Eigenschaften, die bezüglich eines Merkmals unterschieden werden, heißen Merkmalsausprägungen (z.B. männlich, weiblich; 20 Jahre alt). Formal werden hier Merkmale als Abbildungen aufgefaßt, die den Untersuchungseinheiten Zahlen zuordnen; man spricht dann auch von Variablen bzw. Variablenwerten. Die Skaleneigenschaften von Merkmalen legen fest, wie weit man unterschiedliche Werte interpretieren kann bzw. will. Ein Merkmal ist:    -           nominalskaliert (qualitativ), falls die Werte nur zeigen, ob die Untersuchungseinheiten sich voneinander unterscheiden (z.B. Geschlecht, Beruf).    -           ordinalskaliert (Rangmerkmal), falls die Werte eine Reihenfolge oder Rangordnung der Objekte wiedergeben (z.B. bei Bewertungen "gut" - "befriedigend" - "schlecht").    -           metrisch (quantitativ), wenn die Differenz von Werten interpretierbar ist (z.B. Geburtsjahr, Alter, Einkommen). Die Bedeutung der Skaleneigenschaften besteht hauptsächlich darin, Kriterien für den sinnvollen Einsatz von Kennwerten zu geben. Die im nächsten Abschnitt angegebenen Maßzahlen der Streuung und das arithmetische Mittel erfordern metrisches Niveau, die Quantile , größter und kleinster Wert, ordinales Niveau und der Modus ist auch bei nominalskalierten Merkmalen sinnvoll. Weiterhin werden metrische Merkmale nach der Mächtigkeit ihres Wertebereichs unterschieden: Diskrete Merkmale können nur isolierte Zahlenwerte annehmen (z.B. Kinderzahl von Familien), stetige Variablen alle Zahlen eines reellen Intervalls. Merkmale wie z.B. Einkommen oder Gewicht werden als stetige Merkmale aufgefaßt, weil sehr viele und sehr dicht beieinanderliegende Werte möglich sind. Eindimensionale Häufigkeitsverteilungen und ihre Kennwerte. Bei insgesamt n Untersuchungseinheiten bezeichnet xn die Ausprägung des Merkmals X der n-ten Untersuchungseinheit, n=1, ..., n. Die k auftretenden (od. möglichen) verschiedenen Merkmalsausprägungen sind mit xi, i=1, ..., k bezeichnet, wobei bei mindestens ordinalskalierten Merkmalen die xi der Größe nach geordnet sind. Als erster Schritt der Datenaufbereitung ordnet die absolute Häufigkeitsverteilung den Ausprägungen xi die Anzahl ni und die relative Häufigkeitsverteilung den Anteil ni / n der Untersuchungseinheiten zu, die xi als Ausprägung haben. Sie kann z.B. durch ein Säulen- oder Stabdiagramm dargestellt werden. Bei Vorliegen vieler Ausprägungen oder zum Vergleich mit anderen Gesamtheiten erscheint es sinnvoll, die Verteilung summarisch durch Kennwerte zu beschreiben. Einfache Lageparameter sind größter, kleinster und häufigster Wert (Modus, Modalwert). Ein p-Quantil xp teilt die Untersuchungseinheiten so auf, daß etwa (exakt: höchstens) ein Anteil p kleinere und (höchstens) ein Anteil (1p) größere Ausprägungen hat. Die 0,25; 0,5; 0,75-Quantile heißen auch Quartile, x0,5 als ein Mittelwert der Verteilung heißt Median . Die Quartile 1500, 2000 und 3000 eines Merkmals "Einkommen in EUR" sagen z.B. aus, daß jeweils etwa ein Viertel der Untersuchungseinheiten weniger als 1500, zwischen 1500 und 2000, zwischen 2000 und 3000 und mehr als 3000 EUR Einkommen hat. Der gebräuchlichste Lageparameter ist das arithmetische Mittel als Durchschnittswert der Ausprägungen:                       


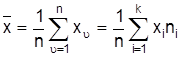
Dem arithmetischen Mittel verwandte Parameter sind gewogenes , geometrisches , harmonisches und quadratisches Mittel  .Die  Angabe mehrerer Parameter (z.B. aller Quartile) gibt Information über die Form der Verteilung oder die Streuung der Daten. Kennwerte der Streuung versuchen diese Information in einer Zahl zusammenzufassen. Einfache derartige Kennwerte sind die Spannweite als Differenz von größtem und kleinstem Wert oder der mittlere Quartilsabstand          1/2 (X0.75 - X0.25). Eine Klasse von Streuungsparametern berechnet sich aus den Abständen der Werte von einem Mittelwert. Aus dieser Klasse wird fast ausschließlich die mittlere quadratische Abweichung (Abweichung) oder Varianz s2 (Varianzanalyse) bzw. Standardabweichung


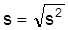
 benutzt:            


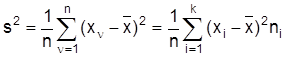
Ein anderer, der Streuung ähnlicher Aspekt bei der Beurteilung von Daten ist die Konzentration. Die Konzentrations- (Konzentration) oder Lorenzkurve oder die zugehörige Maßzahl beschreiben, wie sich die Merkmalssumme auf die Untersuchungseinheiten verteilt, ob z.B. wenige Betriebe einen großen Teil der Arbeitnehmer einer Branche beschäftigen. Bei metrischen Merkmalen wird oft anstelle des exakten Wertes nur angegeben, in welches von k Intervallen die Ausprägung fällt (z.B. wird in Fragebögen zumeist nicht nach dem genauen Einkommen, sondern nur nach der Zugehörigkeit zu bestimmten Einkommensklassen gefragt). Außerdem kann eine Gruppierung von Daten ein erster Schritt zur Informationszusammenfassung sein oder mit Zahlenangaben können genau genommen Intervalle gemeint sein (z.B. die Angabe 10 cm für eine Länge zwischen 9,5 und 10,5 cm). Die Häufigkeitsverteilung ordnet bei gruppierten Daten den Intervallen die absoluten bzw. relativen Häufigkeiten zu. Sie wird durch ein Histogramm (Häufigkeitsdichte) dargestellt: Um wiederzugeben, wie dicht die Werte näherungsweise liegen, wird über jedes Intervall ein Rechteck gezeichnet, dessen Höhe proportional zum Quotienten von Häufigkeit und Breite ist. Bei der (näherungsweisen) Berechnung von Quantilen wird angenommen, die Daten seien gleichmäßig innerhalb der Intervalle verteilt.


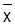
 und s2 werden vereinfachend mit den Intervallmittelpunkten berechnet. Zweidimensionale Häufigkeitsverteilungen und Zusammenhangsmaße. Die Beschreibung der Beziehung zwischen zwei Merkmalen X und Y basiert auf der gemeinsamen Häufigkeitsverteilung, die jeder Ausprägungskombination (xi, yj) ihre Häufigkeit nij (bzw. die relative Häufigkeit nij / n) zuordnet. Man kann sie in einer Kreuztabelle oder Kontingenztafel darstellen:


                       


           


           


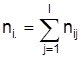
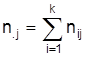
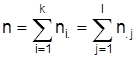
                                               Die eindimensionalen Verteilungen von X und Y heißen nach ihrer Position in der Tabelle auch Randverteilungen. Die Abhängigkeit eines Merkmals X von einem anderen Merkmal Y kann detailliert durch bedingte Verteilungen beschrieben werden, indem getrennte Häufigkeitsverteilungen von X für die durch Y = yj gegebenen Teilmengen aller Untersuchungseinheiten erstellt werden (z.B. Parteipräferenz nach Altersgruppe, Geschlecht usw.). Die bedingte relative Häufigkeitsverteilung von X unter der Bedingung Y=yj ordnet den xi die Zahlen nij / n.j zu. Mittelwerte und andere Kennwerte der bedingten Verteilungen heißen auch bedingte Mittelwerte usw. Merkmale X und Y heißen (statistisch) unabhängig, wenn alle bedingten relativen Häufigkeitsverteilungen von X unter den Bedingungen Y=yj (bzw. von Y unter den Bedingungen X=xi) übereinstimmen. Zusammenhangsmaße, die nur Eigenschaften der Nominalskala ausnutzen, heißen Assoziations- oder Kontingenzkoeffizienten. Diese Kennzahlen beschreiben den Grad der Abhängigkeit mit Zahlen aus dem Intervall [0, 1 und betragen 0 bei Unabhängigkeit. Eine Klasse von Kontingenzkoeffizienten basiert auf dem Vergleich der beobachteten Häufigkeiten nij mit den Werten


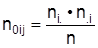
der Indifferenztabelle. Die Indifferenztabelle gibt an, welche Häufigkeiten bei Unabhängigkeit der Merkmale zu erwarten wären. Gebildet wird zunächst die Kenngröße            


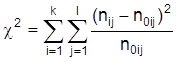
Der maximale Wert


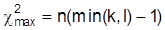
 wird angenommen, wenn bei einem Merkmal jede Ausprägung nur zugleich mit einer einzigen Ausprägung des anderen Merkmals auftritt. Eine Normierung dieses Kennwertes auf den Bereich [0, 1 ist der Kontingenzkoeffizient von Cramér:            


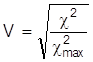
            Die Assoziationskoeffizienten von Goodman und Kruskal gehen von folgendem Denkmodell aus: Man will für alle Untersuchungseinheiten die Ausprägungen des Merkmals X nach bestimmten Regeln einmal mit und einmal ohne Kenntnis der Ausprägung von Y vorhersagen. Die bei Berücksichtigung der Ausprägung von Y ermöglichte relative Fehlerverminderung gilt dann als Maß der Abhängigkeit. Die Abhängigkeit eines metrischen Merkmals X von einem qualitativen Merkmal Y (z.B. Einkommen von Geschlecht) kann durch den Koeffizienten h2 gemessen werden. Er basiert auf einem Vergleich der bedingten Varianzen von X unter den Bedingungen yj mit der Gesamtvarianz von X (vgl. Varianzzerlegung, Varianzanalyse). Ein einfaches Mittel zur Darstellung der gemeinsamen Verteilung zweier metrischer Variablen ist ein Streuungsdiagramm . Jede Untersuchungseinheit wird als Punkt mit den Koordinaten (xn, yn) in ein Koordinatensystem eingezeichnet. Die Regressions - und Korrelationsanalyse bieten Verfahren, eine Gerade möglichst gut an diese Punkte anzupassen und die Güte dieser Anpassung zu beurteilen. Hier sei nur der lineare Korrelationskoeffizient von Bravais-Pearson genannt:                        


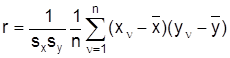
wobei sx und sy die Standardabweichungen von X und Y bezeichnen. Bei r=0 heißen die Merkmale unkorreliert; speziell sind unabhängige Merkmale unkorreliert. Das Vorzeichen von r gibt an, ob die Regressionsgerade positive oder negative Steigung hat. Die Extremwerte ±1 werden angenommen, wenn die Punkte exakt auf einer Geraden liegen. Bei ordinalskalierten Merkmalen wird die Abhängigkeit ebenfalls durch Kennwerte beschrieben, die 0 bei Unabhängigkeit betragen, deren Vorzeichen angibt, ob mit steigenden x-Werten die y-Werte tendenziell steigen oder fallen und die bei perfekter derartiger Beziehung +1 oder 1 als Extremwerte haben. Eine Möglichkeit zur Messung besteht in der Zuordnung von Rangzahlen. Der Untersuchungseinheit mit der kleinsten Ausprägung wird die Rangzahl 1 zugeordnet, der nächstgrößeren 2 usw. Bei Einheiten mit gleichen Ausprägungen werden die entsprechenden Rangzahlen gemittelt. Da Rangzahlen metrisch sind, kann man sinnvoll den linearen Korrelationskoeffizienten von Bravais-Pearson der Rangzahlen bilden; er heißt dann Rangkorrelationskoeffizient von Spearman. Eine andere Möglichkeit zur Messung ordinalen Zusammenhangs besteht im Vergleich aller Paare von Untersuchungseinheiten bezüglich beider Merkmale. Hierauf basieren die Rangkorrelationskoeffizienten von Kendall und von Goodman und Kruskal. Weitere Gebiete der D. Zur Beschreibung der Beziehungen zwischen mehr als zwei Merkmalen sei allgemein auf multivariate Verfahren verwiesen (siehe Regression -, Korrelations -, Varianz -, Clusteranalyse). Die Zeitreihenanalyse untersucht Veränderungen von Merkmalsausprägungen im Lauf der Zeit (z.B. die Entwicklung der Arbeitslosenzahlen in der Bundesrepublik oder des Umsatzes einer Branche). Maß- oder Indexzahlen setzen nach sachlichen Gesichtspunkten verschiedene Kennzahlen durch Quotienten- oder Mittelbildung in Bezug (z.B. Bevölkerungsdichte, Preisindices). Sie werden hier nicht näher behandelt, da bei der Konstruktion und Beurteilung dieser Kennzahlen die inhaltliche Bedeutung der Merkmale primär ist. Zur graphischen Präsentation von Daten sei hier nur auf die entsprechenden Stichworte in den unten angegebenen Encyclopedien verwiesen. Ein relativ neues (bzw. wiederentdecktes) Gebiet der Statistik ist die Explorative Datenanalyse. Wie die D. stellt sie Verfahren der Datenaufbereitung bereit und verzichtet auf die stochastischen Modellannahmen der Induktiven Statistik. Allerdings geht sie im Vergleich zur Deskriptiven Statistik von unbestimmteren Fragestellungen und offeneren Konzepten aus, um Hinweise auf Besonderheiten und unbekannte Strukturen in den Daten zu finden. Dabei läßt sie als Ergebnis auch divergierende Aussagen nebeneinander stehen.

Literatur: F. Ferschl, Deskriptive Statistik. Würzburg-Wien 1978. W. H. Kruskal / J. M. Tanur (Hrsg.), International Encyclopedia of Statistics. New York (insbesondere die Stichworte: Statistics, Descriptive; Graphic Presentation; Data Analysis, Exploratory). S. Kotz / N. L. Johnson (Hrsg.), Encyclopedia of Statistical Sciences. New York 1983 (insbesondere die Stichworte: Graphical Representation, Exploratory Data Analysis).