Inhaltsübersicht I. Gegenstand und Ziel II. Verfahrensablauf am Beispiel der zweifaktoriellen Varianzanalyse III. Mehrdimensionale Varianzanalyse IV. Anwendungsvoraussetzungen V. Stellenwert der Varianzanalyse im Marketing I. Gegenstand und Ziel Die Varianzanalyse (englisch Analysis of Variance, ANOVA) umfasst eine Reihe statistischer Auswertungsverfahren zur Feststellung des Einflusses qualitativer Merkmale und quantitativer Messergebnisse (Hochstädter, D./Kaiser, U. 1988). Ihr Ziel ist die Überprüfung von vermuteten Ursache-Wirkungszusammenhängen zwischen nominalskalierten, unabhängigen und metrisch skalierten abhängigen Variablen. Ergebnis der Varianzanalyse ist die Zurückweisung oder Bestätigung einer angenommenen kausalen Beziehung. Dagegen werden keine Aussagen darüber gemacht, wie die Kausalität beschrieben werden kann. Als Instrument der Überprüfung von Kausalhypothesen ist die Varianzanalyse das wichtigste Verfahren zur Auswertung von Experimenten. Für die Verfahren der Varianzanalyse ist es einerseits von Bedeutung, ob die untersuchte Kausalität durch einen oder durch mehrere ursächliche Faktoren bedingt ist. Nach der Zahl berücksichtigter Faktoren unterscheidet man die einfaktorielle, zweifaktorielle, n-faktorielle Varianzanalyse. Andererseits kann sich eine Ursache auch in mehrfacher Hinsicht auswirken. Untersucht die Varianzanalyse (einen oder mehrere) ursächliche Einflüsse auf gleichzeitig mindestens zwei Wirkungsgrößen, so spricht man von der multiplen oder mehrdimensionalen Varianzanalyse (Abb. 1). 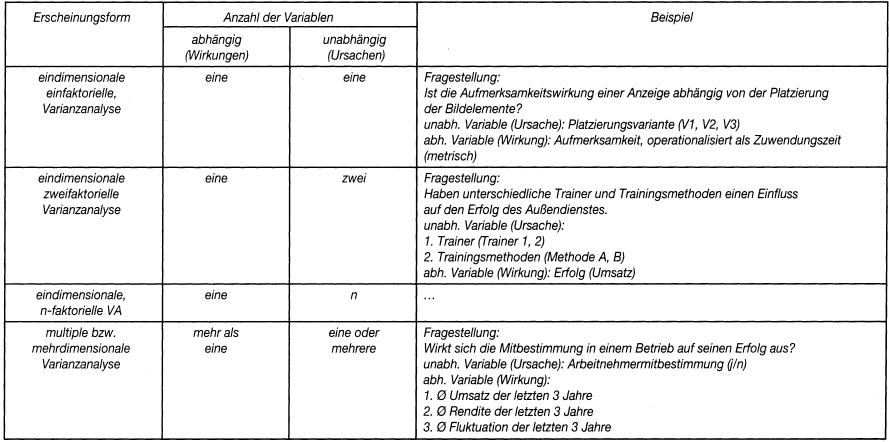Abb. 1: Ausgewählte Erscheinungsformen der Varianzanalyse II. Verfahrensablauf am Beispiel der zweifaktoriellen Varianzanalyse 1. Analytischer Teil Die Logik des Verfahrens soll auf der Grundlage eines Beispiels erläutert werden: Für den Markterfolg von PC-Standardsoftware ist die Bedienerfreundlichkeit wichtig. Deshalb wurden bei der Gestaltung eines Programms drei verschiedene Varianten entworfen, deren Unterschiede ausschließlich im Layout wichtiger Bedienungselemente liegen. Weiter ist anzunehmen, dass auch die farbliche Gestaltung der Bedienungselemente auf dem Bildschirm einen Einfluss auf die Bedienerfreundlichkeit hat. Aus diesem Grunde wurden auch zwei verschiedene Farbvarianten für die Bedienungselemente ausgewählt. Nun ist zu klären, ob sich das Layout und/oder die Farbgestaltung tatsächlich auf die Bedienerfreundlichkeit der Software auswirken. In diesem Beispiel liegen zwei unabhängige Variablen vor: erstens das Maskenlayout X1 mit 3 (allgemein: k = 1, 2, ? K, also K = 3) Abstufungen und zweitens die Farbgestaltung X2 mit 2 (allgemein: v = 1, 2, ? V, also V = 2) Abstufungen. Abhängige Variable Y ist die »Bedienerfreundlichkeit«. Als Indikator hierfür wird die Zeit gewählt, die im Rahmen einer gestellten Aufgabe vom Aufruf einer Maske bis zur Auslösung des nächsten Bedienungsschrittes vergeht. Je kürzer diese Zeitspanne, umso größer ist die Bedienerfreundlichkeit. Für jede Kombination der Einflussfaktoren X1 und X2 werden Stichproben vom Umfang I = 5 (allgemein: i = 1, 2, ? I) durchgeführt. Jeder Stichprobe liegt also eine andere Programmvariante mit einer spezifischen Kombination von Maskenlayout und Farbgestaltung zugrunde. Die Gesamtzahl der Stichproben beläuft sich somit auf 2 * 3 = 6. Man spricht daher auch von einem 2 * 3-faktoriellen Design der Untersuchung. Tab. 1 enthält die einzelnen Stichproben mit ihren Messwerten yikv und den hieraus errechneten Mittelwerten. 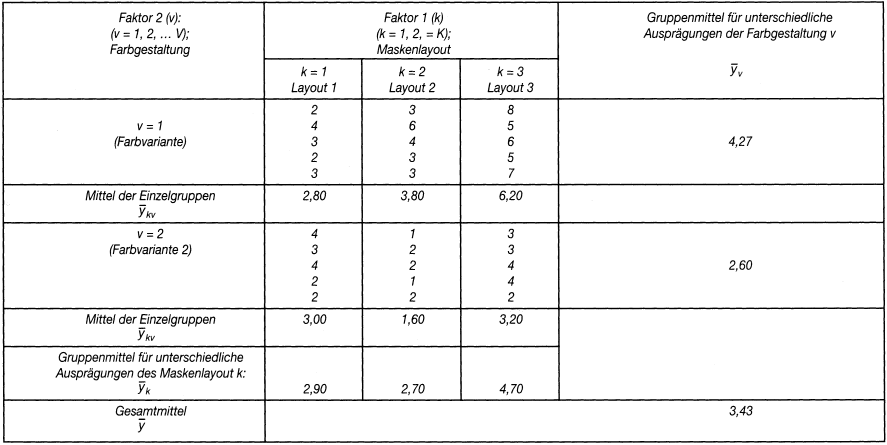Tab. 1: Ausgangswerte zum Beispiel der zweifaktoriellen Varianzanalyse Dabei ist festzustellen, dass die 6 Programmvarianten (oder Stichproben) voneinander abweichende durchschnittliche Bedienungszeiten aufweisen, also einen unterschiedlichen Bedienungskomfort haben (vgl. hierzu die Mittel der Einzelgruppen y¯kv in Tab. 1). Unklar ist jedoch, ob die Unterschiede zwischen den Mittelwerten tatsächlich auf die Veränderung des Layout und/oder der Farbe zurückzuführen sind und kein Ergebnis rein zufälliger Variationen darstellen. Bei dieser Frage geht es nicht nur um den Vergleich der Ergebnisse aus 6 Stichproben. Der logische Kern des Problems zielt vielmehr darauf ab, ob die Stichproben aus derselben Grundgesamtheit stammen: Lassen sich die Mittelwerte als Zufallsergebnisse aus einer einzigen Gesamtheit interpretieren oder muss man annehmen, dass sie aus verschiedenartigen Gesamtheiten stammen? Zur Verdeutlichung: »Bei einer Auswahl von je 10 Nüssen werden in einer ersten Stichprobe 6, in einer zweiten 8 gute Nüsse gefunden. Ist diese Abweichung nun zufällig, weil die Nüsse aus demselben Sack sind, oder hat der Unterschied eine tiefere Bedeutung, weil die Nüsse aus verschiedenen Säcken stammen?« (Swoboda, H. 1971, S. 335). Zur Beantwortung dieser Frage sind die Verteilungen der einzelnen Messwerte näher zu betrachten. Dabei interessiert zunächst die Gesamtstreuung, d.h. das Verhalten der 30 Messwerte gegenüber dem Gesamtdurchschnitt y¯. Der Grund hierfür liegt darin, dass einerseits zufällige, nicht erfasste Faktoren innerhalb der Stichproben und andererseits die bewusst veränderten Faktoren des Maskenlayout und der Farbgestaltung für das Entstehen der Gesamtstreuung verantwortlich sind. Errechnet wird die Gesamtstreuung SSG (mit SS für Sum of Squares, und G für Gesamt) über die quadrierten Abweichungen der Einzelwerte vom Gesamtmittel, die über alle Ausprägungen von k und v sowie die Stichprobeneinheiten i aufsummiert werden (vgl. Tab. 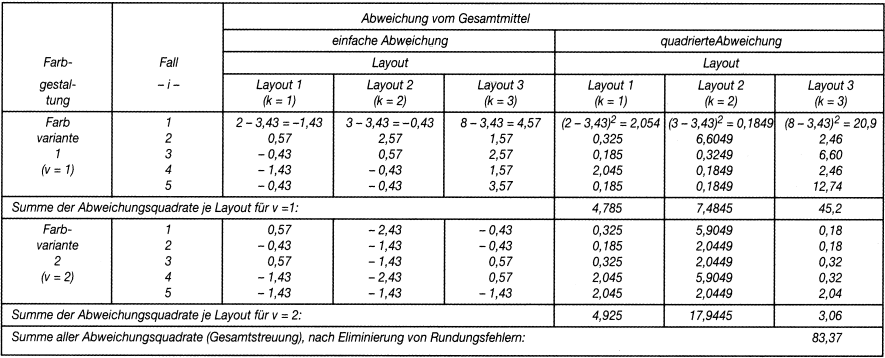2): Tab. 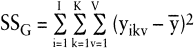2: Die Ermittlung der Gesamtstreuung (1) In der errechneten Gesamtstreuung von 83,37 spiegelt sich nun also die durch nicht kontrollierte Faktoren bedingte zufällige Streuung innerhalb der Stichproben und die »systematische« Streuung zwischen den Stichproben, die durch die Faktoren Maskenlayout und Farbgestaltung ausgelöst wurden. Die zu lösende Aufgabe besteht mithin darin, diese Einflüsse voneinander zu trennen. Hierzu dient die Streuungszerlegung respektive »Varianzanalyse«. Durch sie wird die zufallsbedingte Streuung innerhalb der Stichproben von der systematischen Streuung zwischen den Stichproben getrennt. Nun setzt sich die systematische Streuung bei einem mehrfaktoriellen Design allerdings aus unterschiedlichen Komponenten zusammen. So sind einmal die isolierten Einflüsse von Maskenlayout und Farbgestaltung herauszustellen. Man spricht dabei von Haupteffekten. Ein weiterer Einfluss ergibt sich aus der möglichen Wechselwirkung zwischen den unabhängigen Variablen: Kann es z.B. sein, dass sich die Farbgestaltung bei Maskenlayout 1 in anderer Weise auf die Bedienerfreundlichkeit auswirkt als bei Maskenlayout 2 oder 3? Solche Einflüsse werden Interaktionseffekte genannt. Für die Durchführung der Varianzanalyse bedeutet dies, dass die Gesamtstreuung bzw. die Streuung zwischen den Stichproben in mehrere Bestandteile zu zerlegen ist. So sind jene Streuungsanteile festzustellen, die auf die einzelnen Faktoren und auf die Wechselwirkung zwischen ihnen entfallen (vgl. Abb. 2). Hinsichtlich der Streuungskomponenten wird dabei unterstellt, dass sich diese additiv zur Gesamtstreuung zusammenfassen lassen. Abb. 2: Die Streuungszerlegung bei der zweifaktoriellen Varianzanalyse Zur Streuungszerlegung: Zunächst wird die zufallsbedingte Streuung innerhalb der Stichproben SS1 ermittelt: Hierzu wird in jeder Stichprobe die Summe der quadratischen Abweichungen zwischen den einzelnen Beobachtungswerten und dem zugehörigen Stichprobenmittel gebildet. Hieraus resultieren 6 Summen von Abweichungsquadraten. Diese werden ihrerseits für jede Kombination von k und v aufsummiert. 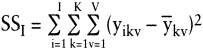Formal gilt: (2) Es resultiert: SS1 = (2 – 2,8)2 + (4 – 2,8)2 + (3 – 2,8)2 + (2 – 2,8)2 + (3 – 2,8)2 + (3 – 3,8)2 + (6 – 3,8)2 + (4 – 3,8)2 + (3 – 3,8)2 + (3 – 3,8)2 + ? ? + ? ? + ? ? = 24,4 Die Summe der systematischen Streuung zwischen den Stichproben kann nun als Differenz zwischen Gesamtstreuung und Streuung »innerhalb« mit SSG – SS1 = 83,37 – 24,40 = 59,97 errechnet werden (vgl. Abb. 2). Sie enthält die »Haupteffekte« Maskenlayout und Farbgestaltung sowie den »Interaktionseffekt« zwischen diesen Faktoren. Bezüglich der Haupteffekte stellt sich die Frage, in welchem Maße ein einzelner Faktor zu Abweichungen vom Gesamtmittel beiträgt. Hierzu kann folgende Überlegung angestellt werden: Die systematische Streuung zwischen den Stichproben bleibt auf jeden Fall erhalten, solange die jeweiligen Stichprobenmittel konstant bleiben. Bestünde nun bei unveränderten Mittelwerten eine zufallsbedingte, stichprobeninterne Streuung von 0, so müsste die Gesamtstreuung identisch der systematischen Streuung zwischen den Stichproben sein. Gerade diese Situation kann aber künstlich geschaffen werden, indem die einzelnen Messwerte 1-mal durch das zugehörige Stichprobenmittel ersetzt werden. Da im Fall der zweifaktoriellen Varianzanalyse jedoch die systematischen Streuungen zwischen den Stichproben für die Haupteffekte interessieren, wird jeder Messwert 1-mal durch das jeweilige Gruppenmittel y¯k bzw. y¯v ersetzt. Somit wird die interne Streuung bei unveränderten »Zwischen«-Streuungen künstlich auf null reduziert. Dieser Zusammenhang ist für den Haupteffekt 1: »Maskenlayout« in Tab. 3 dargestellt; für den Haupteffekt 2: »Farbgestaltung« wäre analog vorzugehen. 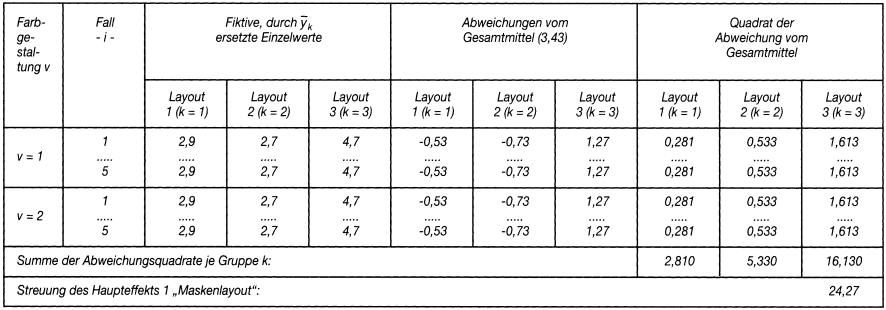Formal gilt für die Streuungen der beiden Haupteffekte: Tab. 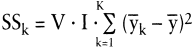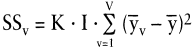3: Die Ermittlung der Streuung von Haupteffekt 1: »Maskenlayout« Zusammenfassend belaufen sich die Streuungen auf 24,27 für das »Maskenlayout« und 20,83 für die »Farbgestaltung«. Als Letztes ist die auf Interaktion von Maskenlayout und Farbgestaltung zurückgehende Streuungskomponente festzustellen. Nach Abb. 2 kann sie bereits als Differenz zwischen der Gesamtstreuung und den bislang ermittelten Streuungen errechnet werden: SSkv = SSG  – SS1  – SSk  – SSv = 83,37 – 24,40 – 24,27 – 20,83 = 13,87 Ihre sachlogische Herleitung beruht auf folgender Überlegung: Um die zufallsbedingte interne Streuung bei unveränderter »Zwischen«-Streuung erneut zu eliminieren, werden in jeder Stichprobe alle Messwerte 1-mal durch das zugehörige Stichprobenmittel y¯kv ersetzt. Zieht man von diesem »künstlichen Zellenwert« die zugehörige layout- und farbbedingte Abweichung vom Gesamtmittel und schließlich das Gesamtmittel selbst ab, so bleibt letztlich eine auf die fiktive Einzelmessung bezogene Abweichung, die durch den Interaktionseffekt zwischen k und v bedingt sein muss. Um hieraus die Streuung zu errechnen, wird diese Einzelabweichung quadriert. Da in jeder Stichprobe (nach den oben getroffenen Annahmen) I-gleiche Einzelmessungen vorgenommen wurden, kann die auf Interaktion bezogene Streuung in der Stichprobe mit dem I-fachen der quadrierten Einzelabweichung ermittelt werden. Diese Streuungen sind für alle sechs Stichproben zu ermitteln und aufzusummieren (vgl. Tab. 4). Formal gilt: Tab. 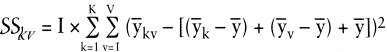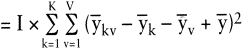4: Die Ermittlung der interaktionsbedingten Streuung Damit ist die Streuungszerlegung im engeren Sinne abgeschlossen. Die ermittelten Größen wurden dabei als Summen von Abweichungsquadraten ausgewiesen. Vor ihrer weiteren Betrachtung werden sie nunmehr standardisiert, d.h. in mittlere Abweichungsquadrate bzw. Varianzen umgerechnet. Hierzu sind sie durch die zugehörige Zahl von Freiheitsgraden (engl.: degrees of freedom, df) zu dividieren. Die Berechnung der Freiheitsgrade ist in Tab. 5, die Berechnung der Varianzen in Tab. 6 zusammengefasst. Tab. 5: Berechnung der Freiheitsgrade für das Beispiel Tab. 6: Berechnung der Varianzen für die zweifaktorielle Varianzanalyse 2. Teststatistischer Teil Wie sind nun die (standardisierten) Ergebnisse der vorgenommenen Streuungszerlegung zu beurteilen? Hierzu gilt: Je größer die systematische, im Beispiel: die durch Layout und Farbgestaltung der Bedienungselemente bedingte Varianz »zwischen«, und je kleiner die zufallsbedingte Varianz »innerhalb« der Strichproben ist, umso eher dürfte die Annahme berechtigt sein, dass die Stichproben tatsächlich unterschiedlichen Gesamtheiten entstammen und somit das Maskenlayout bzw. die Farbgestaltung einen Einfluss auf die Bedienerfreundlichkeit der Software haben. Als letztliche Instanz für die zu findende Antwort dienen teststatistische Grundlagen. Deshalb wird die Varianzanalyse verschiedentlich auch den Testverfahren zugeordnet (Bleymüller, J./Gehlert, G./Gülicher, H. 1992). Geprüft wird H0: »Die Stichproben entstammen der gleichen Gesamtheit; d.h. die Unterschiede zwischen den Mittelwerten sind zufälliger Natur.« Hierzu wird das relative Größenverhältnis der jeweiligen Varianzen »zwischen« und »innerhalb« der Stichproben als empirischer Wert der F-Verteilung gebildet und mit dem theoretischen Wert entsprechend dem gewünschten Signifikanzniveau und der gegebenen Freiheitsgrade verglichen. Liegt der empirische Wert über dem theoretischen, wird die Null-Hypothese abgelehnt. In diesem Fall kann eine signifikante Andersartigkeit der Stichprobenergebnisse angenommen werden. Umgekehrt gilt, dass die Unterschiede zwischen den Mittelwerten dann keine größere Bedeutung haben, wenn der theoretische Wert der F-Verteilung über dem empirischen liegt. Für das Beispiel wird in Bezug auf die Einflussgrößen »Maskenlayout«, »Farbgestaltung« sowie der möglichen Interaktion zwischen diesen getestet. Die Ergebnisse sind in Tab. 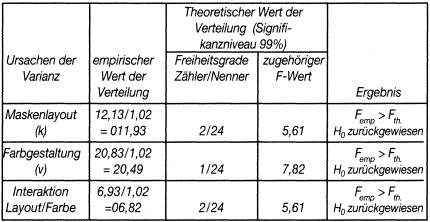7 zusammengefasst: Tab. 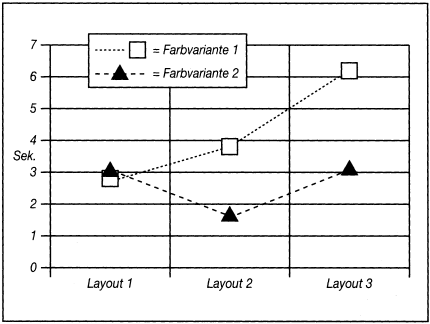7: Die Ergebnisse der zweifaktoriellen Varianzanalyse Abb. 3: Bedienungszeiten in Abhängigkeit von Maskenlayout und Farbgestaltung Die Ergebnisse zeigen: Sowohl das Maskenlayout als auch die Farbgestaltung haben einen signifikanten Einfluss auf die Bedienerfreundlichkeit der untersuchten Software. Auch kann eine gemeinsame Wirkung von Maskenlayout und Farbgestaltung angenommen werden. Zur Interpretation solcher Interaktionseffekte in zweifaktoriellen Modellen der Varianzanalyse sind die Polygonzüge hilfreich, die durch Verbindung der Zellenmittelwerte y¯1v ? y¯Kv mit v = 1, ?,V entstehen (vgl. Abb. 3). Ungefähre Parallelität weist darauf hin, dass keine Interaktion besteht. Nicht parallele Verläufe deuten dagegen Interaktionseffekte an. Abb. 3 verdeutlicht dabei Struktur und Art der Wechselwirkungen. So zeigt sich, dass eine Wechselwirkung zwischen den Farbvarianten sowie Layout 1 und 2 besteht. Während die Farbvarianten bei Layout 1 ähnliche Wirkungen auslösen, ist dies bei Layout 2 nicht der Fall. Weitergehende Fragen, etwa die paarweise Überprüfung der einzelnen Abstufungen eines Faktors oder der paarweise Vergleich einzelner Zellenmittelwerte können durch geeignete Zusatztest beantwortet werden. Die bekanntesten dürften dabei der Duncan-Test, der Schaffé-Test und der Student-Newman-Keuls-Test sein (Zöfel, P. 1992). 3. Varianten der eindimensionalen Varianzanalyse Varianzanalysen sind entsprechend den Gegebenheiten des jeweiligen Untersuchungsdesigns zu variieren. Im Folgenden werden wichtige Varianten skizziert, jedoch nicht näher erläutert. Die zuvor dargestellte Streuungszerlegung beruht u.a. darauf, dass in den einzelnen Stichproben (Zellen) gleich viele Beobachtungen vorliegen Dies war in dem Beispiel mit einem Stichprobenumfang von I = 5 gegeben. Oft entstehen jedoch so genannte unbalancierte Verhältnisse, so durch Ausfälle in einzelnen Stichproben. Auch Kosten-, Zeit- oder Kapazitätsgründe verhindern häufig einen gleichen Stichprobenumfang in den Zellen. Schließlich ist es in hierarchisch angelegten Untersuchungen oft zwangsläufig, dass nachgelagerte Faktoren nicht über gleich viele Stufen verfügen. In all diesen Fällen können Reparametrisierungen vorgenommen werden. Die Auswirkungen auf die Varianzzerlegung sind bei Läuter/Pincus beschrieben (Läuter, H./Pincus, R. 1989), Rechenbeispiele finden sich bei Zöfel (Zöfel, P. 1992). Auch lassen sich neben den bislang beschriebenen »kreuztabellarisch« wirkenden Faktoren »hierarchisch« wirkende Faktoren herausstellen. Dies ist z.B. dann gegeben, wenn eine bestimmte Ausprägung (oder Abstufung) von Faktor 2 nicht mit allen, sondern nur mit einer Ausprägung des Faktors 1 auftreten kann. Beispiel: Es soll festgestellt werden, ob sich alternative Werbemethoden (Faktor 1) in verschiedenen Verkaufsregionen (Faktor 2) auf den Umsatz (abhängige Variable) auswirken. Da in einer Verkaufsregion nur jeweils eine Werbemethode angewandt werden kann, ergibt sich der typische hierarchische Aufbau: Bestimmte Zerlegungsergebnisse der Streuung entsprechend der kreuztabellarischen Einflussanalyse ergeben dann keinen Sinn. Insofern ist die methodische Vorgehensweise der Varianzanalyse zu korrigieren (Läuter, H./Pincus, R. 1989). Eine weitere Variante der Varianzanalyse bezieht sich darauf, dass nicht immer alle Abstufungen eines Faktors untersucht werden können. In diesem Falle müsste aus der Reihe der möglichen Faktorabstufungen eine Zufallsstichprobe gezogen werden. Man spricht in diesem Fall auch von randomisierten Effekten. Als Beispiel sei erwähnt, dass der Einfluss von Vertriebsleiter-Persönlichkeiten auf Leistungen von Außendienstmitarbeitern untersucht werden soll. Wie auch immer das Konstrukt der »Persönlichkeit« abgegrenzt sein mag, so kann doch jeder einzelne Vertriebsleiter als Abstufung dieses Einflussfaktors betrachtet werden. Da jedoch nicht alle Vertriebsleiter in eine Untersuchung einbezogen werden können, muss eine Zufallsauswahl getroffen und schließlich ein Rückschluss auf die Verkaufsleiterpersönlichkeit im Allgemeinen gezogen werden (Ritsert, J./Stracke, E./Heider, F. 1976). III. Mehrdimensionale Varianzanalyse Während die ein-, zwei- bzw. n-faktorielle Varianzanalyse von nur einer abhängigen Variablen ausgeht, wird bei der multiplen Varianzanalyse der gleichzeitige Einfluss eines oder mehrerer unabhängiger Faktoren auf mehrere abhängige Größten untersucht. Beispiel: Alternative Entlohnungssysteme (unabhängiger Faktor) bewirken einerseits einen Leistungsanreiz, der sich auf Umsatzergebnisse von Verkaufsmitarbeitern (1. abhängige Variable) auswirkt. Andererseits können hieraus auch Verkaufspraktiken entstehen, die Reaktanz bei den Kunden auslösen und zu negativen Imagewirkungen beitragen (2. abhängige Variable). Bei der Prüfung einer solchen Hypothese könnten die Wirkungen auf Umsatzergebnisse und Image zunächst isoliert untersucht werden. Gerade die vermutete wechselseitige Abhängigkeit lässt es jedoch zweckmäßig erscheinen, eine simultane Wirkungsuntersuchung vorzunehmen. Die multivariate Betrachtung der Abhängigkeiten führt häufig zu Ergebnissen, die bei Anwendung der eindimensionalen Varianzanalyse im Verborgenen bleiben. Andererseits können zur Differenzierung von Gruppen unwichtige Faktorausprägungen durch Nivellierung den Blick auf andere, wichtige Faktorausprägungen versperren (zur multiplen Varianzanalyse vgl. Ahrens, H./Läuter, J. 1981; Läuter, H./Pincus, R. 1989). IV. Anwendungsvoraussetzungen Die an die Anwendung der Varianzanalyse geknüpften Voraussetzungen beruhen auf der mathematisch-statistischen Axiomatik des Verfahrens. Sie lassen sich wie folgt zusammenfassen: 1.  Skalenniveau: Die Varianzanalyse setzt voraus, dass die in der vermuteten Kausalität untersuchten Ursachen (unabhängige Variablen) kategorialer Natur sind, als in Form einer Nominalskala vorliegen. Die Wirkungsgrößen (abhängige Variablen) müssen dagegen metrisch skaliert sein. Die Forderung nach dem Nominalskalenniveau der unabhängigen Variablen ist dabei nicht restriktiv, da eine beliebig skalierte Variable immer auf Nominalskalenniveau reduziert werden kann. 2.  Additivität: Wie die Ausführungen unter II. gezeigt haben, geht das hier behandelte lineare Modell der Varianzanalyse bei der Streuungszerlegung von einer Additivität der einzelnen Wirkungskomponenten aus: So kann jeder einzelne Beobachtungswert in der erläuterten zweifaktoriellen Varianzanalyse yikv als Summe des arithmetischen Mittels in der Grundgesamtheit (Μ), der Wirkung des Faktors 1 (αk), des Faktors 2 (βv), der Interaktion von Faktor 1 und 2 (αβ)kv und der Wirkung nicht kontrollierter Zufallseinflüsse (εikv) dargestellt werden. yikv = Μ + αk + β + (αβ)kv + εikv Diese Annahme ist sicher dann erfüllt, wenn die Werte von y unabhängig voneinander gewonnen werden. Hierzu sind die Elemente der Gesamtstichprobe nach dem Zufallsprinzip auszuwählen und auf die Untersuchungszellen aufzuteilen. 3.  Normalverteilungs-Axiom: Viele statistische Testverfahren beruhen auf der Annahme der Normalverteilung. Diese beinhaltet letztlich, dass die Messwerte der zugrunde liegenden Merkmalsverteilungen (nahezu) unabhängig voneinander entstehen und im Wesentlichen keine Ausreißer enthalten. Nach dem zentralen Grenzwertansatz folgt hieraus, dass derartige Merkmalsverteilungen näherungsweise normalverteilt sind. Auch der F-Test, der in der Varianzanalyse eingesetzt wird, setzt voraus, dass die Stichproben aus normalverteilten Gesamtheiten zufällig gezogen wurden. Aus diesem Grunde wird »Normalverteilung« auch für die Varianzanalyse gefordert. Ist sie nicht gegeben, kann der F-Test zu verzerrten Ergebnissen führen. In der Regel werden dabei signifikante Testwerte leichter erreicht. Insofern sollte der empirische den kritisch-theoretischen F-Wert deutlich überschreiten. Sofern Zweifel an normalverteilten Populationsdaten bestehen, sind diese zur Vermeidung fehlerhafter Schlussfolgerungen zu beseitigen. Hierzu können der Chiquadrat-Test, der Kolmogoroff-Smirnow-Test und (bei weniger als 20 Werten) der Nullklassentest herangezogen werden (Hartung, J./Elpelt, B./Klösener, K.-H. 1993). Für die eindimensional-einfaktorielle Varianzanalyse kann auf diese Prüfung verzichtet werden, wenn anstelle des F-Tests verteilungsunabhängige Alternativen wie der Kruskal-Wallis-Test oder der Friedman-Test Anwendung finden. Für mehrfaktorielle Designs stehen solche Alternativen jedoch kaum zur Verfügung. 4.  Varianzhomogenität: Die Forderung nach der Varianzhomogenität bedeutet, dass sich die Varianzen in den einzelnen Stichproben nicht signifikant voneinander unterscheiden dürfen, sie müssen statistisch vergleichbar sein. Genauer ausgedrückt: Sie sollten »nicht stärker voneinander abweichen, als es einer Irrtumswahrscheinlichkeit von p = 0,01 entspricht« (Zöfel, P. 1992, S. 240). Da für die Varianzen innerhalb der Stichproben die zufälligen, in einer Untersuchung nicht kontrollierten Einflüsse verantwortlich sind, beinhaltet die Forderung nach Varianzhomogenität, dass die Zufallseinflüsse in allen Zellen gleichermaßen zur Geltung kommen müssen. Damit ist diese Anforderung gleichbedeutend mit homogenen, also übereinstimmenden Versuchsbedingungen außerhalb der kontrollierten Einflussfaktoren. Es ist einleuchtend, dass dies eine Voraussetzung für die Interpretierbarkeit der Ergebnisse darstellt. Allerdings ist diese Anforderung mitunter schwer zu realisieren. Heterogenität der Varianzen bewirkt, dass kausale Beziehungen tendenziell eher angenommen werden (genau die gegenteilige Aussage findet sich bei Kerlinger (Kerlinger, F. 1978). Dies bedeutet, dass der F-Wert etwas überhöht ausgewiesen wird. Aus diesem Grunde »sollte man mit p = 0,01 testen, um ein faktisches Signifikanzniveau von p = 0,05 zu erhalten« (Zöfel, P. 1992, S. 36). Studien zur Abschätzung des Fehlers bei Varianzheterogenität haben ergeben, dass bei einem Verhältnis von s2max/s2min≈ 10 eine reichliche Verdoppelung des Signifikanzniveaus eintritt (Glaser, W. R. 1978). Bei annähernd gleichen Stichprobenumfängen in den Zellen kann die Voraussetzung der Varianzhomogenität mit dem Hartley- und dem Cochran-Test geprüft werden. Bei verschieden großen Stichprobenumfängen eignet sich der rechenintensive Bartlett-Test. V. Stellenwert der Varianzanalyse im Marketing Die Varianzanalyse kennzeichnet immer dann ein außergewöhnlich wichtiges Verfahren der statistischen Datenanalyse, wenn im Rahmen der Untersuchung von Kausalitäten keine funktional gesicherte Vorstellung über die Beziehungen zwischen verursachenden und Ergebnisvariablen vorliegen. Das Gleiche gilt, wenn die verursachenden Größen nicht quantitativ messbar, sondern nur qualitativ beschreibbar sind. Gerade solche Analysesituationen sind in der empirischen Marketingforschung häufig gegeben. Zunächst kommt dabei der Varianzanalyse unter wissenschaftstheoretischem Aspekt im Begründungszusammenhang von Hypothesen und Theorien besondere Bedeutung zu. Dies gilt insbesondere für die verhaltenswissenschaftliche Forschung im Marketing. Auch in der Marketingpolitik tritt die skizzierte Analysesituation häufig auf. So stellt sich immer wieder die Frage, ob ein veränderter Einsatz oder veränderte Einsatzkombinationen von Marketinginstrumenten Einfluss auf relevante Ergebnisgrößen haben. Mit ihrer Beantwortung trägt die Varianzanalyse zur Optimierung des Instrumentaleinsatzes im Marketing bei. Da die Varianzanalyse das zentrale Instrument der Auswertung von Experimenten darstellt, kann die Frage nach ihrem Stellenwert nicht unabhängig von der Bedeutung der Experimente im Marketing gesehen werden. Dabei haben in den letzten Jahren insbesondere drei Tendenzen eine deutliche Zunahme der experimentellen Forschung und damit eine steigende Bedeutung der Varianzanalyse bewirkt: Erstens ist Statistiksoftware in großem Umfang insbesondere auch für PC-Anwendungen verfügbar (Sarnow, K. 1994; Bankhofer, U./Bausch, T. 1991). Das Rechnen, nicht nur von Varianzanalysen, ist damit immer einfacher geworden und stellt keinen Engpass mehr dar. Zweitens wurde die Durchführung von Feldtests im Marketing aufgrund veränderter und regional weitaus besser abgrenzbarer Kommunikationsinstrumente erheblich einfacher und kostengünstiger. Drittens ist die Gewinnung von Experimentalinformationen gerade in der Konsumentenforschung durch den Einsatz moderner Kassensysteme im Handel extrem vereinfacht und verbilligt worden. Literatur: Ahrens, H. : Varianzanalyse, Berlin 1968 Ahrens, H./Läuter, J. : Mehrdimensionale Varianzanalyse, 2. A., Berlin 1981 Backhaus, K./Erichson, B./Plinke, W. : Multivariate Analysemthoden, 7. A., Berlin et al. 1993 Bankhofer, U./Bausch, T. : Elf Statistikprogramme im Vergleichstest, in: PC-Magazin, H. 15/1991, S. 45 – 52 Berekoven, L./Eckert, W./Ellenrieder, P. : Marktforschung, 6. A., Wiesbaden 1993 Bleymüller, J./Gehlert, G./Gülicher, H. : Statistik für Wirtschaftswissenschaftler, 8. A., München 1992 Böhler, H. : Marktforschung, 2. A., Stuttgart et al. 1992 Bortz, J. : Lehrbuch der Statistik für Sozialwissenschaftler, 4. A., Berlin 1993 Crowder, M. J./Hand, D. J. : Analysis of repeated measures, London 1990 Fisher, R. A. : Statistical Methods for Research Workers, 1. A., Edinburgh et al. 1925 Glaser, W. R. : Varianzanalyse, Stuttgart et al. 1978 Hartung, J./Elpelt, B./Klösener, K. H. : Statistik, 9. A., München et al. 1993 Heiberger, R. M. : Computation for the analysis of designed experiments, New York 1989 Hochstädter, D./Kaiser, U. : Die Varianzanalyse, in: WISU, 1988, S. 665 – 669 Kerlinger, F. : Grundlagen der Sozialwissenschaften, 1. Bd., 2. A., Weinheim et al. 1978 Köhler, W./Schachtel, G./Volesek, P. : Biostatistik, 2. A., Berlin 1992 Läuter, H./Pincus, R. : Mathematisch-statistische Datenanalyse, München 1989 Marinell, G. : Multivariate Verfahren, 3. A., München et al. 1990 Maxwell, S. E./Delany, H. D. : Designing experiments and analysing data, Belmont 1990 Meffert, H. : Marktforschung, Wiesbaden 1986 Montgomery, D. C. : Design and analysis of experiments, 3. A., New York 1991 Nollau, H. : Statistische Analysen, Basel 1979 o. V., : Marktübersicht Statistiksoftware, in: PC-Magazin, H. 16/1991, S. 54 – 55 Pruscha, H. : Angewandte Methoden der mathematischen Statistik, Stuttgart 1989 Ritsert, J./Stracke, E./Heider, F. : Grundzüge der Varianz- und Faktorenanalyse, Frankfurt a.M. et al. 1976 Sarnow, K. : Abstraktionsinstrumente, in: ct Magazin für Computer Technik, H. 3/1994, S. 174 – 188 Saville, D. J./Wood, G. R. : Statistical Methods, New York et al. 1991 Schlittgen, R. : Einführung in die Statistik, 4. A., München 1993 Swoboda, H. : Exakte Geheimnisse, München et al. 1971 Unger, F. : Marktforschung, Heidelberg 1989 Zöfel, P. : Univariate Varianzanalysen, Stuttgart et al. 1992