Lorenzkurve

Für die Messung und graphische Darstellung der personellen Einkommensverteilung wurde von Pareto, Gibrat, Lorenz und anderen Autoren eine Reihe von statistischen Verteilungsmaßen entwickelt. Dabei dient regelmäßig die Normal- oder die Gleichverteilung der Einzeleinkommen als Vergleichsgrundlage. In Abb. 1 demonstriert die Glockenkurve A eine Normalverteilung, in Abb. 2 die Diagonale A eine Gleichverteilung der individuellen Einkommen . Die in Abb. 1 durch die Glockenkurve A dargestellte Normalverteilung ist eine symmetrische Häufigkeitsverteilung . Auf der Waagrechten ist die absolute Höhe des Einzeleinkommens (y), auf der Senkrechten die absolute Zahl der Personen (n) abgetragen, die ein Einkommen dieser Höhe beziehen. Bei einer Normalverteilung ist der häufigste Wert der Einzeleinkommen unter der Annahme ymin = 0 gleich der Hälfte des maximalen Einzeleinkommens.                        


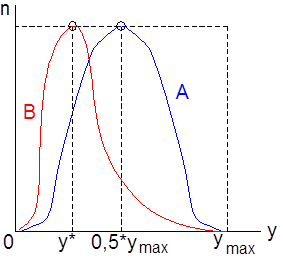
Die tatsächliche personelle Einkommensverteilung weicht regelmäßig von der Normalverteilung ab. In Abb. 1 ist die Häufigkeitsverteilung B asymmetrisch. Sie ist im Vergleich zur Glockenkurve A linkssteil od., was dasselbe besagt, sie ist rechtsschief. Die Kurve B ist im Vergleich zur Normalverteilung A nach links gestaucht. Der häufigste Wert der Einzeleinkommen (y*) ist derart kleiner als die Hälfte des maximalen individuellen Einkommens (ymax). Die häufigsten Einzeleinkommen liegen also in Wirklichkeit nicht im mittleren, sondern im unteren Drittel der Einkommensskala. Diese Tatsache findet in den Theorien der personellen Einkommensverteilung zahlreiche Begründungen. In Abb. 2 wird die durch die L. B abgebildete faktische Verteilung nicht, wie in Abb. 1, mit der Normalverteilung verglichen, sondern mit der Gleichverteilung, dargestellt durch die Diagonale A.                        


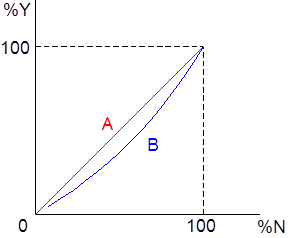
Auf der Waagrechten ist der prozentuale Anteil (%N) der Zahl aller Personen, deren Einkommen zwischen Null und einem bestimmten Wert liegt, an der Gesamtzahl (N) aller Einkommensbezieher abgetragen, auf der Senkrechten der prozentuale Anteil (%Y) dieser Personen am gesamten Volkseinkommen (Y). Dabei werden die Individuen "von unten nach oben" kumuliert. Wären alle Einzeleinkommen gleich, dann würde die L. B mit der Diagonalen A zusammenfallen. Bei Gleichverteilung hätten x% der Einkommensbezieher immer auch x% des Volkseinkommens. Die faktische Einkommensverteilung ist aber keine Gleichverteilung: Die L. verläuft unterhalb der Diagonalen, und die Abweichung zwischen beiden Kurven ist umso größer, je stärker die Einzeleinkommen voneinander abweichen. Als Maß für die faktische Ungleichheit der Einzeleinkommen kann darum das Verhältnis der Fläche zwischen den Kurven A und B zur Fläche unter A genommen werden. Dieses Verteilungsmaß ist der Gini -Koeffizient. Der Gini-Koeffizient ist bei Gleichverteilung gleich Null und bei extremer Ungleichverteilung gleich eins. Je größer also der Gini-Koeffizient, umso größer die Abweichung der faktischen Verteilung von der Gleichverteilung der individuellen Einkommen.

Literatur: G. Blümle, Theorie der Einkommensverteilung. Eine Einführung. Berlin-Heidelberg-New York 1975.