Maximum-Likelihood-Methode

eine Methode zur Konstruktion von Schätzfunktionen für statistische Parameter, die gegenüber anderen Verfahren zu präferieren ist, da Maximum-Likelihood-(ML-) Schätzfunktionen unter ziemlich allgemeinen Voraussetzungen günstige statistische Eigenschaften aufweisen: Konsistenz (und daher asymptotische Erwartungstreue), relative Effizienz, asymptotische Normalverteilung der Schätzfunktionen bei großen Stichproben (n ® ¥) . ML-Schätzer für beliebige Parameter Q (z.B. Mittelwert, Varianz , Koeffizienten in der Regressionsanalyse) erhält man prinzipiell gemäß folgendem Vorgehen: Die Likelihood-Funktion L(Q|x1, ..., xn) eines gegebenen Stichprobenergebnisses (x1, ..., xn)  für eine Zufallsvariable X wird, soweit L differenzierbar ist, für den Parameter Q maximiert; für alle möglichen Werte für Q wird somit der Wert


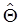
 als Parameterschätzer ausgewählt, für den L, die Wahrscheinlichkeit des Auftretens der vorliegenden Stichprobe, maximal wird. Der ML-Schätzer


 ist daher eine Funktion der Stichprobenwerte:


= d(x1, ..., xn) . Das gleiche Verfahren wird im Falle mehrerer zu schätzender Parameter angewendet; anstelle der Likelihood-Funktion wird i.d.R. die Logarithmusfunktion lnL maximiert, da sie ihr Maximum an der gleichen Stelle hat.