|
Spieltheorie
Inhaltsübersicht
I. Gegenstand und Entwicklung der Spieltheorie
II. Darstellung von Spielen
III. Gleichgewichtskonzepte
IV. Strategisches Denken
I. Gegenstand und Entwicklung der Spieltheorie
Die Spieltheorie betrachtet Situationen, in denen zwei oder mehr Individuen als sog. „ Spieler “ unabhängig voneinander Entscheidungen treffen. Das Besondere dabei ist, dass der Erfolg eines jeden Spielers nicht nur von seiner eigenen Entscheidung, sondern auch von denen seiner Mitspieler abhängt. Als interaktive Entscheidungstheorie erweitert die Spieltheorie somit die Analyse rein individueller Entscheidungsprobleme. Wie die individuelle Entscheidungstheorie unterstellt sie dabei in der Regel, dass jeder einzelne Spieler rational bestrebt ist, seine erwartete „ Auszahlung “ (Nutzen, Gewinn) zu maximieren. Neben dieses traditionelle Optimierungskalkül tritt in der Spieltheorie aber auch ein strategisches Kalkül, da jeder Spieler bei seiner Entscheidung das Verhalten und die Reaktion der anderen Spieler zu berücksichtigen hat. Beispiele für interaktive Entscheidungssituationen sind neben den bekannten Gesellschaftsspielen (Schach, Poker, etc.) das Wettbewerbsverhalten von Unternehmen, das Bietverhalten in einer Auktion, Verhandlungsprobleme, Konflikte zwischen Tarifparteien sowie Entscheidungsprozesse in verschiedenen Teilbereichen einer Organisation. Der Beitrag der Spieltheorie zur Analyse solcher Situationen umfasst zwei Aspekte: Zum einen bietet sie formale Modelle zur Beschreibung interaktiver Entscheidungsprobleme. Dies beinhaltet nicht nur die Darstellung der „ Spielregeln “ , d.h. der Aktionsmöglichkeiten oder Strategien der einzelnen Spieler, sondern auch die Beschreibung ihrer Präferenzen und ihrer Information über das Spiel und seinen Verlauf. Zum anderen macht die Spieltheorie Aussagen über das zu erwartende Ergebnis eines Spiels, indem sie Gleichgewichtskonzepte für das strategische Verhalten der beteiligten Spieler verwendet.
Die moderne Spieltheorie beginnt in den ersten Jahrzehnten des zwanzigsten Jahrhunderts mit der Analyse von Glücks- und Gesellschaftsspielen (vgl. Borel, Emile 1921; Neumann, John von 1928; Zermelo, Ernst 1913). Diese Ansätze finden ihren Höhepunkt in dem durch John von Neumann und Oskar Morgenstern im Jahre 1944 veröffentlichten Buch „ Theory of Games and Economic Behavior “ (Neumann, John von/Morgenstern, Oskar 1944). Die in diesem Buch entwickelte Theorie ist jedoch auf sog. Nullsummenspiele beschränkt, bei denen die Summe der Gewinne aller Spieler stets gleich Null ist. Gerade in vielen ökonomischen Situationen ist aber der Gewinn eines Spielers nicht automatisch gleich dem Verlust seiner Gegenspieler: Durch kooperatives Verhalten können sich möglicherweise alle Spieler verbessern, und in manchen Konfliktsituationen ist denkbar, dass sie alle einen Verlust erleiden.
Die Tatsache, dass sich die Spieltheorie zur heute dominanten Methodik für die Analyse ökonomischer Interaktionen weiterentwickelt hat, beruht auf Fortschritten, zu denen insb. die drei Nobelpreisträger für Ökonomie des Jahres 1994 – John Harsanyi, John Nash und Reinhard Selten – beigetragen haben: Das von John Nash entwickelte Gleichgewichtskonzept ist nicht auf die Lösung von Nullsummenspielen beschränkt und wird heute allgemein als „ Nash-Gleichgewicht “ bezeichnet (vgl. Nash, John 1950). Auf Reinhard Selten gehen Verfeinerungen des Gleichgewichtskonzepts von Nash zurück; so eliminiert sein Kriterium der „ Teilspielperfektheit “ unglaubwürdiges Verhalten bei dynamischen strategischen Interaktionen (vgl. Selten, Reinhard 1965). Ein von John Harsanyi vorgeschlagener Ansatz erlaubt es, auch Spiele mit unvollständiger Information zu betrachten (vgl. Harsanyi, John 1967). In solchen Spielen ist der einzelne Spieler nicht genau über die Präferenzen und strategischen Möglichkeiten seiner Gegenspieler informiert, z.B. kennt der einzelne Bieter in einer Auktion ja nicht die Zahlungsbereitschaft der anderen Bieter oder im Marktwettbewerb haben die beteiligten Unternehmen im Allgemeinen keine vollständige Information über die Produktionskosten der Konkurrenten.
Die Gleichgewichtskonzepte der „ nicht-kooperativen “ Spieltheorie unterstellen individuelles Optimierungsverhalten in Situationen, in denen die Beteiligten keine bindenden Vereinbarungen über ihr Verhalten treffen können. Rationales Verhalten kann aber auch aus Modellen evolutionärer Selektion resultieren, in denen nur erfolgreiche Verhaltenstrategien den evolutionären Prozess überstehen. Die „ evolutionäre “ Spieltheorie betrachtet solche Selektionsmechanismen nicht nur in der Biologie sondern auch in der Wirtschaftswissenschaft (vgl. Maynard Smith, John 1982). Ein weiterer Bereich der modernen Spieltheorie, dessen zunehmende Bedeutung durch die Verleihung des Nobelpreises Vernon Smith, Vernon im Jahre 2002 gewürdigt wurde, ist die „ experimentelle “ Spieltheorie. Sie untersucht in kontrollierten Laborexperimenten das Verhalten von Individuen in interaktiven Entscheidungssituationen, um theoretische Aussagen der Spieltheorie zu überprüfen oder auch um Einsichten in „ beschränkt rationale “ Verhaltensweisen zu gewinnen.
II. Darstellung von Spielen
Die Spieltheorie bietet zwei Formen der Darstellung einer interaktiven Entscheidungssituation: Die „ Normalform “ beschreibt eine solche Situation auf statische Weise, indem sie davon ausgeht, dass die beteiligten Spieler ihre Strategien simultan und unabhängig voneinander wählen. In der „ Extensivform “ wird die dynamische Struktur eines Spiels, d.h. die Reihenfolge der Entscheidungen der einzelnen Spieler, durch einen „ Spielbaum “ verdeutlicht.
1. Die Normalform
Die Beschreibung eines Spiels in der Normalform beinhaltet die Menge der Spieler, deren strategische Möglichkeiten und ihre Auszahlungen in Abhängigkeit vom Ausgang des Spiels. Als Beispiel wird in Abb. 1 das berühmte „ Gefangenendilemma “ dargestellt, in dem sich zwei Gefangene befinden, die einer gemeinsamen Straftat verdächtigt werden. Für einen vollständigen Tatbeweis ist jedoch das Geständnis zumindest eines Gefangenen erforderlich. Jeder der beiden Gefangenen hat die zwei Strategien „ Gestehen (G) “ und „ Nicht Gestehen (N) “ . Die möglichen vier Strategiekombinationen und die resultierenden Auszahlungen werden in Abb. 1 beschrieben: Wenn beide Spieler nicht gestehen, erhalten sie aufgrund der vorhandenen Evidenz jeder eine Haftstrafe von einem Jahr, d.h. eine Auszahlung in Höhe von – 1. Falls sie beide gestehen, erwartet jeden eine Haft von 6 Jahren. Gesteht nur einer der beiden Gefangenen die Tat, wird er dafür durch seine Freilassung belohnt und der andere hat eine Haftstrafe von 9 Jahren zu verbüßen.
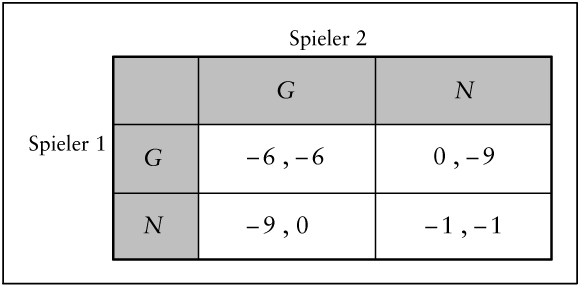
Abb. 1: Das Gefangenendilemma
Das Gefangendilemma spiegelt die Struktur vieler sozialer Konfliktsituationen wider, bei denen die Beteiligten die Wahl zwischen kooperativem (N) und nichtkooperativem Verhalten (G) haben. Abb. 2 dagegen verdeutlicht ein Koordinationsproblem, bei dem die beiden Spieler das Problem haben, sich unabhängig voneinander zwischen den Strategien A und B zu entscheiden. Eine positive Auszahlung erhalten beide Spieler nur dann, wenn ihre Entscheidungen übereinstimmen. Dabei zieht Spieler 1 aber eine Koordination auf A und Spieler 2 eine Koordination auf B vor.
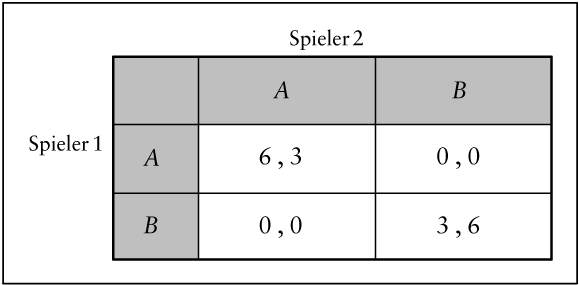
Abb. 2: Ein Koordinationsproblem
2. Die Extensivform
Die Extensivform beschreibt die Reihenfolge, in der die Spieler am Zug sind, durch einen Spielbaum. An den einzelnen Entscheidungsknoten hat der jeweils betroffene Spieler eine Aktion zu wählen. Am Ende des Spielbaums geben die Endknoten die Auszahlungen der Spieler in Abhängigkeit vom Verlauf des Spiels an. In Abb. 3 entscheidet ein Unternehmen als Spieler 1 zunächst darüber, ob es in den Markt eintritt (E) oder nicht (N). Spieler 2 ist ein Unternehmen, das bisher alleine den Markt beherrscht hat. Er kann auf den Markzutritt entweder aggressiv (A) oder friedfertig (F) reagieren. Die Auszahlungen an den Endknoten zeigen, dass Spieler 1 bei der Wahl von E einen Gewinn in Höhe von 2 realisiert, wenn Spieler 2 sich für F entscheidet. Dagegen führt der Marktzutritt zu einem Verlust von – 1 bei einer aggressiven Reaktion des Spielers 2. Spieler 2 erzielt den Gewinn 4, wenn der Konkurrent nicht in den Markt eintritt. Sollte dieser aber E wählen, so ist es für Spieler 2 besser, sich für F zu entscheiden.
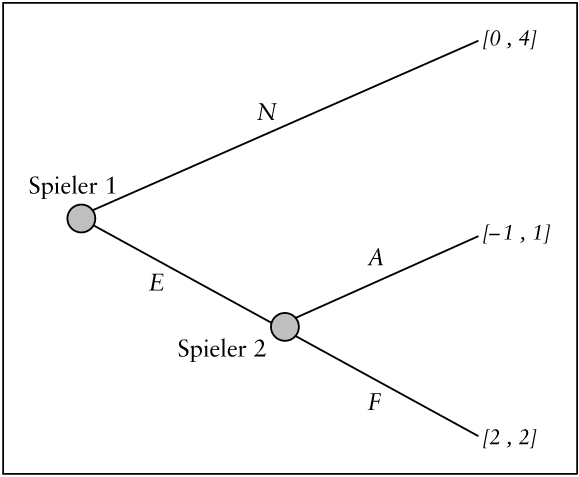
Abb. 3: Marktzutritt
Unvollkommene Information über den bisherigen Verlauf des Spiels lässt sich dadurch berücksichtigen, dass verschiedene Entscheidungsknoten eines Spielers zu einer „ Informationsmenge “ zusammengefasst werden. Eine solche Informationsmenge wird in Abb. 4 durch das gestrichelte Rechteck angedeutet: Sie symbolisiert, dass Spieler 2 nicht weiß, ob Spieler 1 zuvor N oder G gewählt hat. Folglich muss Spieler 2 an dieser Informationsmenge an beiden Entscheidungsknoten dieselbe Aktion wählen; er kann seine Entscheidung nicht vom Verhalten seines Gegenspielers abhängig machen. Es ist leicht zu sehen, dass das Spiel in Abb. 4 äquivalent zu dem Spiel in Abb. 1 ist. In beiden Situationen trifft jeder Spieler seine Wahl von N oder G ohne die Entscheidung des anderen Spielers zu kennen, und für jede Kombination von Strategien sind die Auszahlungen der Spieler in Abb. 1 und Abb. 4 identisch.
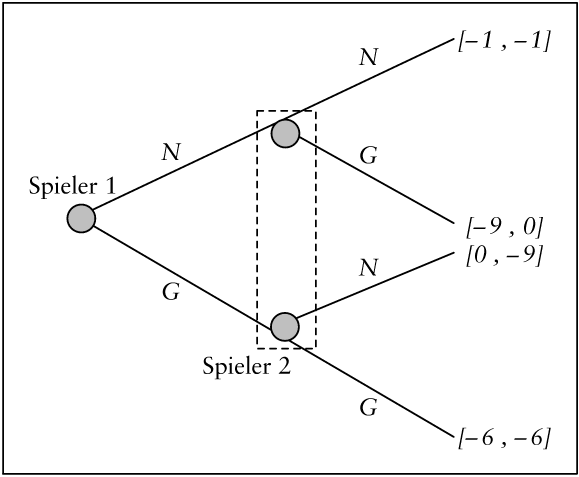
Abb. 4: Unvollkommene Information
Mit Hilfe von Informationsmengen lässt sich auch Unsicherheit der Spieler über bestimmte Tatbestände des Spiels beschreiben. Dazu wird die „ Natur “ als ein künstlicher Spieler eingeführt, der entsprechend einer allgemein bekannten Zufallsregel den Zustand des Spiels bestimmt. Wenn ein Spieler das Ergebnis dieser zufälligen Wahl nicht kennt, agiert er unter Unsicherheit. Auf diese Weise kann man z.B. berücksichtigen, dass jeder Spieler zwar seine eigenen Auszahlungen kennt, dass er aber unvollkommene Information über die Auszahlungen der anderen Spieler hat.
III. Gleichgewichtskonzepte
Die Spieltheorie beschreibt optimierendes Verhalten in einer interaktiven Situation durch Gleichgewichtskonzepte. Dabei setzt sie voraus, dass das Spiel und seine Regeln unter den Beteiligten allgemein bekannt sind.
1. Nash-Gleichgewicht
In dem in Abb. 1 dargestellten Gefangenendilemma ist nahezu offensichtlich, wie ein optimierender Spieler sich verhalten sollte: Falls er erwartet, dass sein Gegenspieler G wählt, beträgt seine Auszahlung – 6 bei der Wahl von G bzw. – 9 bei der Wahl von N. Falls der Gegenspieler N wählt, resultiert aus der Wahl von G die eigene Auszahlung 0, während die Strategie N nur eine Auszahlung in Höhe von – 1 bietet. Unabhängig davon, wie der Gegenspieler sich entscheidet, ist es also immer besser, selbst die Strategie G zu wählen. Diese Strategie ist eine „ dominante “ Strategie. Beachtenswert ist, dass im Ergebnis beide Spieler G wählen, obwohl sie so eine geringere Auszahlung erhalten, als wenn sie sich beide für N entschieden. Dieser Konflikt zwischen individuellem Rationalitätsverhalten und allgemeiner Wohlfahrt kennzeichnet eine Vielzahl ökonomischer Probleme.
Das Kriterium der Dominanz lässt sich nur auf eine beschränkte Klasse von Spielen anwenden. So versagt es z.B. bei dem Spiel in Abb. 2, da hier die optimale Entscheidung jedes Spielers davon abhängt, welche Strategiewahl er bei seinem Gegenspieler vermutet. Aus diesem Grunde verwendet die Spieltheorie in der Regel das allgemeinere Lösungskonzept des „ Nash-Gleichgewichts “ : Eine Strategiekombination, d.h. die Spezifikation einer Strategie für jeden Spieler, stellt ein Nash-Gleichgewicht dar, wenn kein Spieler sich durch einseitige Änderung seines Verhaltens besser stellen kann. Gegeben das Verhalten der Gegenspieler verhält sich also jeder Spieler optimal.
Offensichtlich ist im Gefangenendilemma in Abb. 1 die Strategiekombination G-G das einzige Nash-Gleichgewicht. Jede der anderen drei möglichen Kombinationen würde zumindest einem der beiden Spieler einen Anreiz bieten, auf seine dominante Strategie G auszuweichen. Das Nash-Gleichgewicht bietet aber nicht in allen Spielen eine eindeutige Voraussage. So ist in dem in Abb. 2 dargestellten Koordinationsproblem sowohl A-A wie auch B-B ein Nash-Gleichgewicht. Diese beiden Strategiekombinationen sind stabil, da jeder Spieler bei einseitigem Abweichen eine geringere Auszahlung, nämlich Null, erhält.
Auch das Marktzutrittspiel in Abb. 3 hat zwei Gleichgewichte: So ist E-F ein Gleichgewicht, da Unternehmen 1 durch den Marktzutritt (E) einen Gewinn erzielen kann, wenn Unternehmen 2 friedfertig (F) reagiert. Umgekehrt ist es für Unternehmen 2 besser F als A zu wählen, wenn Unternehmen 1 tatsächlich in den Markt eintritt. Aber auch N-A ist ein Nash-Gleichgewicht des Marktzutrittspiels, denn bei einer aggressiven Reaktion (A) von Unternehmen 2 steht sich Unternehmen 1 bei N besser als bei E. Andererseits ist es für Unternehmen 2 optimal, sich für A zu entscheiden, da diese Entscheidung keine Rolle spielt, solange Unternehmen 1 ohnehin nicht in den Markt eintritt.
2. Rückwärtsinduktion und Teilspielperfektheit
In extensiven Spielen mit vollkommener Information lässt sich ein Nash-Gleichgewicht auch mit dem Verfahren der „ Rückwärtsinduktion “ ermitteln. Dazu ermittelt man zuerst das optimale Verhalten der Spieler an den letzten Entscheidungsknoten. Gegeben dieses Verhalten, lassen sich die optimalen Aktionen der betreffenden Spieler an den vorletzten Entscheidungsknoten ableiten. Wenn man diese Prozedur bis zum Anfangsknoten des Spiels fortsetzt, hat man für jeden Entscheidungsknoten eine optimale Aktionswahl der einzelnen Spieler bestimmt.
Die Anwendung des Prinzips der Rückwärtsinduktion auf das Marktzutrittspiel in Abb. 3 impliziert, dass Spieler 2 auf der letzten Stufe des Spiels F wählt; dadurch erhält er nämlich die Auszahlung 2, während die Wahl von A nur die Auszahlung 1 bietet. Spieler 1 wird sich daher auf der ersten Stufe für E entscheiden und so die Auszahlung 2 realisieren, weil er bei Wahl von N nur eine Auszahlung in Höhe von Null erreichen kann. Das Prinzip der Rückwärtsinduktion selektiert also das Nash-Gleichgewicht E-F. Das andere Gleichgewicht N-A dagegen ist nicht mit Rückwärtsinduktion kompatibel. In der Tat erscheint dieses Gleichgewicht weniger plausibel, da die Wahl von A für Spieler 2 nur solange optimal ist, wie Spieler 1 sich aufgrund dieser Drohung für N entscheidet. Falls Spieler 1 sich nicht durch diese Drohung abschrecken lässt, E zu wählen, wird Spieler 2 doch lieber mit F statt mit A reagieren. In diesem Sinne stellt die Strategie A eine unglaubwürdige Drohung dar.
Das „ teilspielperfekte “ Nash-Gleichgewicht stellt eine Verallgemeinerung des Prinzips der Rückwärtsinduktion dar. Für extensive Spiele fordert es rationales Verhalten im Sinne des Nash-Gleichgewichts nicht nur für den gesamten Spielbaum, sondern auch für alle „ Teilspiele “ , d.h. alle Teilbereiche des Spielbaums, die selbst wieder die Struktur eines Spielbaums haben. Es eliminiert unglaubwürdiges Verhalten auch an solchen Entscheidungsknoten, die im Verlaufe des Spiels nicht erreicht werden. Eine Erweiterung dieser Überlegung des teilspielperfekten Gleichgewichts ist das „ sequentielle “ Gleichgewicht, welches optimales Verhalten auch an Informationsmengen beinhaltet, an denen der betreffende Spieler seine Entscheidung unter unvollkommener Information zu treffen hat (vgl. Kreps, David/Wilson, Robert 1982).
IV. Strategisches Denken
Die Spieltheorie ist ein wichtiges Hilfsmittel zur Analyse von Situationen, in denen zwei oder mehr Individuen interdependente Entscheidungen treffen. Sie bietet aber keinen mechanischen Algorithmus für Handlungsanweisungen oder Voraussagen über das Ergebnis sozialer Interaktion. Vielmehr stellt sie eine Methodik zur Verfügung, welche den Anwender in der Kunst strategischen Denkens und Handelns schult (vgl. z.B.: Dixit, Avinash/Nalebuff, Barry 1991; McMillan, John 1992; Schelling, Thomas 1960).
Strategisches Denken beginnt mit dem Verständnis der interaktiven Situation. Der einzelne Spieler sollte sich nicht nur über seine eigenen Handlungsmöglichkeiten im Klaren sein, sondern auch überlegen, wie seine Gegenspieler die Situation sehen und welche strategischen Möglichkeiten und Anreize sie haben. Bei einer mehrstufigen Interaktion spielen die Reihenfolge und der Informationsstand der Beteiligten eine wichtige Rolle. Auch kann es einen Unterschied machen, ob es sich um ein einmaliges oder ein wiederholtes Spiel handelt, da in der letzteren Situation auch Reputationseffekte auftreten können.
Die Entscheidung für eine Strategie wird in der Regel davon abhängen, welche Strategiewahl den Gegenspielern unterstellt wird. Bei seinen Erwartungen über das Verhalten der anderen Spieler sollte ein Spieler sich stets von dem Gedanken leiten lassen, dass diese ebenso wie er selbst bestrebt sind, möglichst erfolgreich zu sein. In einem dynamischen Spiel ist es unerlässlich, vorausschauend zu denken und entsprechend dem Prinzip der Rückwärtsinduktion sowohl die Reaktionen der Gegenspieler wie auch die eigenen zukünftigen Aktionen in das eigene Kalkül einzubeziehen.
Möglicherweise können ein oder mehrere Spieler auch die Spielregeln zu ihren Gunsten ändern, indem sie z.B. legal bindende Abmachungen treffen. So wird die Interaktion zwischen den Mitgliedern eines Unternehmens durch die Regelung von Entscheidungsbefugnissen und den Zugang zu Informationen und Vermögensgegenständen beeinflusst. In vertragstheoretischen Anwendungen der Spieltheorie dient das Verständnis strategischer Kalküle dazu, optimale Organisationsformen zu analysieren.
Literatur:
Borel, Emile : La Theorie du Jeu et les Equations Integrales a Noyau Symetrique, in: Comptes Rendus de l\'Academie des Sciences, Jg. 173, 1921, S. 1304 – 1308
Dixit, Avinash/Nalebuff, Barry : Thinking Strategically, New York et al. 1991
Harsanyi, John : Games with Incomplete Information Played by Bayesian Players, I: The Basic Model, in: Man.Sc., Jg. 14, 1967, S. 159 – 182
Kreps, David/Wilson, Robert : Sequential Equilibria, in: Econometrica, Jg. 50, 1982, S. 863 – 894
Maynard Smith, John : Evolution and the Theory of Games, Cambridge 1982
McMillan, John : Games, Strategies and Managers, New York et al. 1992
Nash, John : Equilibrium Points in n-Person Games, in: Proceedings of the National Academy of Science USA, Jg. 36, 1950, S. 48 – 49
Neumann, John von : Zur Theorie der Gesellschaftsspiele, in: Mathematische Annalen, Jg. 100, 1928, S. 295 – 320
Neumann, John von/Morgenstern, Oskar : Theory of Games and Economic Behavior, Princeton 1944
Schelling, Thomas : The Strategy of Conflict, Cambridge 1960
Selten, Reinhard : Spieltheoretische Behandlung eines Oligopolmodells mit Nachfrageträgheit, in: Zeitschrift für die gesamte Staatswissenschaft, Jg. 12, 1965, S. 301 – 324
Zermelo, Ernst : Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels, in: Proceedings Fifth International Congress of Mathematicians, Jg. 2, 1913, S. 501 – 504
|