Identifikationsproblem

1. Das I. ist ein Problem empirisch ausgerichteter Wissenschaften, die einen Realitätsausschnitt durch eine mit zunächst unbekannten Parametern in Modellform (Modell) vorliegende Theorie erklären wollen. Dieser Ausschnitt wird durch eine oder mehrere beobachtbare Variable repräsentiert, die durch Meßfehler bedingt den Charakter von Zufallsvariablen haben. Dadurch und durch Hinzunahme latenter Variablen, um Fehler in den Modellgleichungen auszudrücken, wird das Erklärungsmodell zu einem durch eine Verteilung charakterisierten stochastischen Modell. Unterstellt wird die korrekte Spezifikation des Modells, die man nach erfolgreicher Lösung des Identifikationsproblem und der Parameterschätzung anhand diverser Tests feststellen kann. Das Modell S enthält alle Strukturen S, die aufgrund von Vorkenntnissen zur Erklärung des Realitätsausschnitts relevant und zulässig sind. Eine Struktur ist eine ganz bestimmte, durch Wertezuweisung für alle Modellparameter festgelegte Ausprägung des Modells. Das Modell ist die Menge seiner Strukturen. Jede Struktur legt eindeutig einen empirischen Sachverhalt fest, der in Form von Variablen beobachtbar ist. Das I. besteht nun darin, festzustellen, ob umgekehrt die Beobachtung des Sachverhalts ausreicht, die sie erzeugende Struktur S innerhalb des Modells zweifelsfrei zu bestimmen (identifizieren


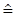
 etwas genau wiedererkennen, lt. Duden).
2. Das I. wird häufig nur als Problem simultaner Gleichungssysteme in der Ökonometrie angesehen; es ist aber allgemeiner. Seien


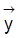
 ein Beobachtungsvektor, der von der gemeinsamen Dichte


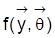
erzeugt sein soll, und


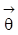
 ein Vektor unbekannter Parameter aus einem Parameterraum W. Definition 1: Zwei Strukturen


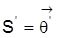
 und


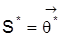
 in W heißen beobachtungsäquivalent, wenn


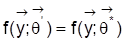
 für alle


. Definition 2: Die Struktur


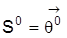
 in S heißt (global) identifizierbar, wenn es keinen anderen Vektor


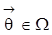
 gibt, der zu


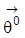
 beobachtungsäquivalent ist. In den Anwendungen ist man oft nur an einem Teil


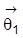
 von


 interessiert. Man betrachtet dann die Zerlegung 


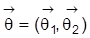
 und der Wert


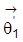
 heißt identifizierbar, wenn es keine zulässigen Werte


,


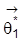
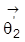
 und


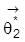
 mit


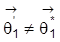
 gibt, für die


 .
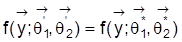
3. Als Beispiel seien die monatlichen Verkaufszahlen zweier Automobiltypen betrachtet, die mit gleicher Varianz s2 normalverteilt sein sollen: X1 ~ n(m1: s2), X2 ~ n(m2: s2). Beobachtet sind nur die summierten Verkaufszahlen beider Typen: yt = x1t + x2t; t = 1, ..., T. Unter der Voraussetzung der Unkorreliertheit von X1 und X2 und deren Autokorrelationsfreiheit lautet die gemeinsame, die Daten generierende Dichte:         


. Zu jedem Wertepaar


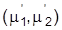
, für das


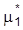
 und


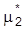
 so gewählt werden, daß 


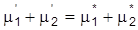
, ergibt sich


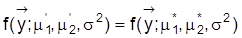
, so daß keine Werte von m1und m2 identifizierbar sind. Hingegen sind alle Werte von s2 identifizierbar. Unterstellt man m1 = m2 =: mY und


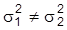
, so ist nun mY identifizierbar, aber wegen


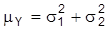
 keine der Varianzen. Ist keine funktionale Beziehung zwischen m1, m2,


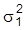
 und


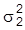
 bekannt, so sind weder die Erwartungswerte noch die Varianzen identifizierbar. In weiterer Abwandlung des Beispiels sei eine Relation zwischen Erwartungswerten und Varianzen, z.B.


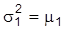
 und


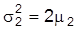
 unterstellt. Der Erwartungswert der Beobachtungsvariablen Y ist noch immer m1 + m2 = mY , und es scheint, als ob m1 und m2nicht identifizierbar sind, da es unendlich viele Paare


 mit


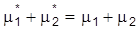
 gibt. Da jedoch für die Varianz von Y gilt:


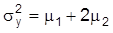
, existiert kein von


 abweichendes Paar, das denselben Erwartungswert mY und dieselbe Varianz


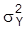
 liefert wie (m1, m2), so daß m1 und m2 identifizierbar sind.  Am vorstehenden Beispiel erkennt man, was auch allgemein nachzuweisen ist, daß Identifizierbarkeit durch Aufstellung von genügend vielen Restriktionen und damit durch Einschränkung des Modells S erreichbar ist. Liegen zu wenig Restriktionen vor, spricht man von Unter- oder Nichtidentifizierbarkeit und eine Parameterschätzung ist unangebracht. Bei Überidentifikation hat man zu viele Restriktionen, und es hängt dann vom jeweiligen Schätzverfahren ab, ob es den Informationsüberfluß durch Reduktion oder geeignete Kombination verarbeitet.
4. Hinsichtlich der Identifizierbarkeit der Parameter des klassischen linearen Regressionsmodells (Regressionsanalyse) gilt: Satz 1: Im linearen Modell


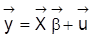
 mit


,


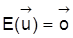
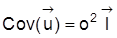
 mit


 als Einheitsmatrix und


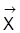
 als fester Designmatrix sind die Varianz


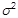
 stets und die Regressionskoeffizienten


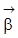
 dann identifizierbar, wenn


 vollen Rang hat. Der Beweis ist einfach. Die Verteilung der Daten hat


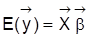
 und


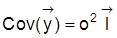
. Man sieht sofort, daß es keine zwei verschiedenen Werte von s2 mit ein und derselben Kovarianzmatrix


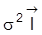
 für


 geben kann. Zum Beweis der Identifizierbarkeit von


 sei angenommen, es gäbe zwei Werte


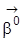
 und


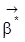
 mit gleichem


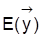
, d.h.


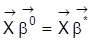
. Dann ist


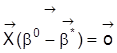
. Hat


  vollen Rang, folgt


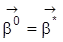
, so daß verschiedene Werte von


 nicht denselben Erwartungswert von


 induzieren können. Hat


 jedoch einen Rangabfall, so spricht man von perfekter Multikollinearität der Regressoren, und es gibt


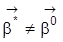
 mit


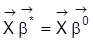
. Bei perfekter Multikollinearität ist


 nicht identifizierbar.
5. Die reduzierte Form


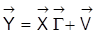
 zu einem ökonometrischen Modell mit Strukturform


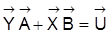
 und


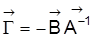
 sowie


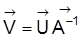
 besteht aus einer Anzahl scheinbar nicht in Relation zueinander stehender linearer Regressionsmodelle mit gemeinsamer Designmatrix


. Aus Satz 1 folgt die Identifizierbarkeit der reduzierte-Form-Parameter in


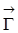
 bei vollem Rang von


.  Für die Identifizierbarkeit der Strukturform-Parameter in


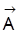
 und


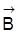
 erweist sich der folgende Satz 2 als nützlich. Satz 2: Wenn


 ein Vektor identifizierbarer Parameter ist und j eine eindeutige Funktion von q, etwa


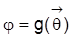
, dann ist auch j identifizierbar. Zum Beweis von Satz 2 betrachte man zwei verschiedene Werte j´ und j* aus dem Wertebereich von g. Da g eindeutig ist, müssen auch die zu j´ und j* gehörenden Werte von


 verschieden sein, und da


  identifizierbar ist, können die zu j´ und j* gehörenden Verteilungen nicht gleich sein, so daß j identifizierbar ist, wenn er als eindeutige Funktion der reduzierte-Form-Parameter zu schätzen ist. Auf dieser Aussage basieren in der Ökonometrie die üblichen Identifikationskriterien, wie z.B. die Rang- und Abzählkriterien (vgl. Rinne, 1976).

Literatur: R. Bowden, The Theory of Parametric Identification. Econometrica 41, 1973, 1069-1074. F. M. Fisher, The Identification Problem in Econometrics. New York, 1966. H. Rinne, Ökonometrie. Stuttgart, 1976. T. J. Rothenberg, Identification in Parametric Models. Econometrica 39, 1971, 577-591.