Ökonometrie

wissenschaftliches Teilgebiet der Ökono­mie, das sich mit ökonomisch-mathemati- schen Modellen mit dem Ziel befaßt, ökono­mische Theorien bzw. Modelle empirisch zu testen und zu schätzen. Dazu bedient sie sich mathematisch-statistischer Methoden, die z.T. Grundlagen der Multivariatenanaly- se in der Marktforschung bilden.

  ist ein Teilgebiet der Wirtschaftswissenschaften, das sich von anderen Teilgebieten nicht durch die zentralen Fragestellungen unterscheidet, wie z.B. die Wirtschaftstheorie von der Wirtschaftspolitik (Theorie der Wirtschaftspolitik), sondern durch die benutzten Begründungsverfahren. Ihr Ziel ist es, ökonomische (Einzel) -Hypothesen und Theorien quantitativ zu spezifizieren und empirisch zu prüfen; d.h., es sollen anhand von allgemein verbindlicher Information, z.B. von Daten der Wirtschaftsstatistik, die Parameter quantitativer ökonomischer Hypothesen und Theorien numerisch bestimmt  geschätzt  und es soll geprüft werden, ob die postulierten Hypothesen und Theorien bzgl. bestimmter Bereiche der ökonomischen Umwelt zutreffen. Diese Hypothesen und Theorien stammen z.T. aus der Wirtschaftstheorie, z.T. werden sie in der Angewandten Ökonometrie entwickelt. Damit eine quantitative Hypothese oder Theorie empirisch geprüft werden kann und ihre Parameter geschätzt werden können, müssen sie als ökonometrische Modelle formuliert werden. Dabei entsprechen ökonometrischen Einzelgleichungsmodellen einzelne Hypothesen und ökonometrischen Mehrgleichungsmodellen (ganze) Theorien. Am Beispiel eines einfachen Einzelgleichungsmodells sollen einige wichtige Begriffe eingeführt werden. Die Keynessche Konsumhypothese (Keynessche Theorie), gemäß der der reale private Konsum einer Periode t, Ct, im wesentlichen vom realen verfügbaren Einkommen derselben Periode, Yt, abhängt, wird als lineares ökonometrisches Modell formuliert.
(1)        Ct = a + bYt + ut      t = 1, 2, ..., T  Da die Keynessche Konsumhypothese nur für eine Gesellschaft mit freier Konsumwahl und Geldwirtschaft gültig sein kann, stellt die Vorgabe des Zeitintervalls [1, T eine Randbedingung für die Gültigkeit des Modells dar.
(1) ist ein Beispiel für ein ökonometrisches Einzelgleichungsmodell
(2)        Yt = f (x1t, x2t, ..., xnt)         t = 1, 2, ..., T Yt heißt abhängige oder endogene Variable oder Regressand. Die x1, x2, ...xn heißen unabhängige oder exogene Variable oder Regressoren, weil sie nicht durch das Modell erklärt  also nicht abhängig von anderen Modellvariablen bestimmt  werden. a und b bzw. die entsprechenden Größen der Funktion f heißen Parameter. ut ist eine Zufallsvariable und heißt Störvariable. Durch sie werden die nicht explizit beachteten  in ihrem Einfluß auf den Regressanden vernachlässigbaren  Variablen zusammengefaßt. Häufig wird f als linear postuliert. Die Störvariable ut muß nicht additiv mit den Regressoren verknüpft sein, ist es jedoch regelmäßig, wenn f linear ist. Die Parameter a und b (bzw. die entsprechenden Parameter bei einer bestimmten Spezifikation von f) sind typischerweise unbekannt, auch wenn man aufgrund von a-priori Information das Vorzeichen und die Größenordnung der Parameter vermuten kann (für
(1) gilt 0 £ a, 0 < b £ 1). Sie müssen also bestimmt  geschätzt  werden. Dafür hat die ökonometrische Methodenlehre, aufbauend auf der statistischen Schätztheorie, Schätzverfahren entwickelt. Diese sind wesentlich abhängig von den Eigenschaften der Störvariablen ut. Ist f in
(2) linear, sind die x1, x2, ..., xn deterministische Variable, und gilt E (ut) = 0, Var (ut) = s2, für alle t , und         


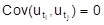
  für ti¹ tj dann bildet
(2) zusammen mit den angegebenen Eigenschaften von ut ein Klassisches Lineares Regressionsmodell (KLR). Die Parameter eines KLR können mit der Kleinst-Quadrate-Methode (KQ-Methode) erwartungstreu, effizient und konsistent geschätzt werden. Besitzen die ut nicht KLR-Eigenschaften, so müssen andere Schätzmethoden benutzt werden, z.B. die gewichtete KQ-Methode. Nachdem die Parameter eines ökonometrischen Modells geschätzt sind, ist es auch numerisch spezifiziert. Dann kann es, falls es richtig ist, zur Prognose unter Umständen als Grundlage wirtschaftspolitischer Entscheidungen herangezogen werden. Bei der Parameterschätzung wird vorläufig unterstellt, daß das postulierte ökonometrische Modell richtig ist. Nach der Schätzung der Parameter muß dies jedoch geprüft werden. Dazu stehen statistische Tests und eher heuristische Verfahren zur Verfügung. Das nach der Schätzung der Parameter auch numerisch spezifizierte ökonometrische Modell wird als "globale" Hypothese, als potentielle Antwort auf eine ökonomische Fragestellung betrachtet. Diese "Gesamthypothese" impliziert einzelne Hypothesen, die statistischen Tests unterworfen werden können. Während das Modell im gesamten durch eher heuristische Verfahren geprüft werden kann, z.B. durch ex-post und ex-ante Prognosen, graphische Darstellungen, Deduktionen aus dem Modell und deren Prüfung, Konsistenzprüfung u.a., lassen sich durch das Gesamtmodell implizierte Einzelhypothesen statistischen Tests unterwerfen. Diese betreffen hauptsächlich das Problem, ob die einzelnen Regressoren einen systematischen Einfluß auf den Regressanden haben, weiter die funktionale Spezifikation und die Eigenschaften der Störvariablen. Solche Tests sind der F-Test, t-Test, Durbin-Watson-Test, Test auf Konstanz der Varianz der Störvariablen u.a. Viele der ausgeführten Überlegungen gelten entsprechend auch für Mehrgleichungsmodelle, besonders was die Spezifikation und empirische Prüfung angeht. Allerdings gibt es nur sehr wenige statistische Tests für Mehrgleichungsmodelle. Zwischen ökonometrischen Einzel- und Mehrgleichungsmodellen bestehen jedoch vorwiegend in Hinsicht auf die statistischen Schätzverfahren wesentliche Unterschiede. Darauf soll im folgenden an einem Standardbeispiel exemplarisch eingegangen werden. Gemäß der Keynesschen Konsumfunktion hängt der Konsum Ct vom Einkommen Yt ab. Weil das Einkommen einer Periode t per definitionem gleich dem Wert der produzierten Konsum- und Investitionsgüter Ct und It ist, gilt für alle betrachteten Perioden
(3)        Yt = Ct + It. Nimmt man an, daß die Investitionen It nicht vom Einkommen Yt oder dem Konsum Ct abhängen, also bzgl. der beiden Beziehungen
(1) und
(3) exogen bestimmt sind, so folgt aus
(1) und
(3), daß Yt und ut korreliert sind: Nach
(1) hängt Ct von ut ab, nach
(3) Yt von Ct, folglich ist Yt eine Funktion von ut. Damit ist Yt eine Zufallsvariable und Yt und ut sind korreliert. Als Folge davon lassen sich mit der Kleinst-Quadrate-Methode a und b nur verzerrt und nicht konsistent schätzen. Wie man sich leicht vorstellen kann, tritt der beschriebene Sachverhalt bei umfangreichen Mehrgleichungsmodellen regelmäßig auf. Modelle dieser Art nennt man simultane oder interdependente Gleichungssysteme. Die ökonometrische Methodenlehre hat für solche Systeme geeignete Schätzverfahren entwickelt. Bei Mehrgleichungssystemen stellt sich oft schwerwiegend das Identifikationsproblem. Es besteht in der Frage, ob und unter welchen Bedingungen die Parameter eines Modells eindeutig geschätzt werden können. Ohne weitere Annahmen oder a-priori Information lassen sich z.B. bei einem Wettbewerbsmodell die Parameter der Angebots- und Nachfragefunktion mit den Daten (pi, qi), i = 1, 2, ..., wobei pi der Preis eines bestimmten Gutes ist und qi die bei diesem Preis abgesetzte Menge ist, nicht eindeutig schätzen  nicht identifizieren. Die Auffassung, daß ökonomische Hypothesen und Theorien empirisch geprüft werden müssen, hat die Angewandte Ökonometrie entstehen lassen. Sie ist ein Teilgebiet der Empirischen Wirtschaftsforschung, in der nicht nur ökonometrische Methoden i.e.S. zur empirischen Prüfung von ökonomischen Hypothesen und Theorien herangezogen werden, sondern auch andere Verfahren, z.B. aus der Statistik.

Literatur: Zur Ökonometrischen Methodenlehre: J. Heil, Einführung in die Ökonometrie.
4. A., Wien, München 1991. H. Schneeweiß, Ökonometrie.
3. A., Würzburg 1978. P. Schönfeld, Methoden der Ökonometrie, 2 Bde. München 1969, 1971. Zur Angewandten Ökonometrie: R. F. Wynn/K. Holden, An Introduction to Applied Econometric Analysis. London 1974.