Schätzverfahren

siehe   Ökonometrie, insbes.   a)


1. Ziel von S. ist die Gewinnung von Aussagen über unbekannte, aber numerisch ausdrückbare Aspekte von Zufallsvariablen . S. stützen sich u.a. auf eine Stichprobe der in Rede stehenden Zufallsvariablen. Das Resultat eines S. ist also auch zufällig, womit klar ist, daß nicht der individuelle Ausgang einer Schätzung beurteilbar ist, sondern nur das Verfahren als solches. Man kann S. einteilen nach    -     dem zu schätzenden Sachverhalt,    -     den verwendeten Informationen,    -     dem methodischen Ansatz,    -     ihren stochastischen Eigenschaften.
2. Geschätzt werden können:          -           künftige Realisationen der Zufallsvariablen (Diese Art der Schätzung heißt Prognose .)          -           Der Umfang und  - bei einem kardinal-extensiven Merkmal - die Merkmalssumme einer endlichen Gesamtheit (Diese Art der Schätzung heißt Hochrechnung und wird in der Stichprobentheorie behandelt.)          -           Funktionen, die das Verteilungsgesetz der Zufallsvariablen beschreiben (Zu nennen sind die Dichte , geschätzt durch z.B. das Histogramm, die Wahrscheinlichkeitsfunktion, geschätzt durch relative Häufigkeiten, und die Verteilungsfunktion, geschätzt durch kumulierte relative Häufigkeiten als Treppen- oder Polygonfunktion.)          -           Funktionalparameter (Das sind Momente der verschiedensten Art wie z.B. der Erwartungswert m, die Varianz s2 oder der Korrelationskoeffizient r, Perzentile wie z.B. Median und Quartile.)          -           Funktionsparameter von Zufallsvariablen mit parametrischer Verteilung (In der Dichte der Weibull-Verteilung sind der Lokalisationsparameter a, der Skalierungsparameter b und der Formparameter c zu schätzende Funktionsparameter.)                        



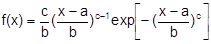
3. Relevante Informationen für ein S. lassen sich in eine von drei Klassen einordnen: Stichprobendaten, Priorinformationen, potentielle Konsequenzen. Für eine Schätzung stets erforderlich sind Stichprobendaten, i.e. in einer Zufallsstichprobe aus der relevanten Verteilung in Form eines Stichprobenvektors x anfallende Beobachtungen. Die klassische Schätztheorie (R. A. Fisher, Karl und E. S. Pearson, J. Neyman) arbeitet ausschließlich mit Stichprobendaten. I.d.R. hat die Stichprobe einen festen, prädeterminierten Umfang n, während man bei sequentiellen S. einen zufälligen Stichprobenumfang hat, d.h. man bricht mit dem Stichprobenziehen beim Erreichen einer gewünschten Schätzgenauigkeit ab. Unter Priorinformationen versteht man das Vorwissen und Vorkenntnisse aus dem früheren Umgang mit dem relevanten oder einem ähnlichen, eng verwandten Vorgang. Gelegentlich hat man auch nur Vermutungen. Die Priorinformation konkretisiert sich bei Schätzung eines stetigen Parameters q in der Festlegung einer Prior-Dichte:


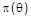
 für


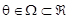
. Bayes-Schätzverfahren basieren auf Stichprobendaten, ausgedrüt durch die Stichprobendichte F(x|q), und Priorinformationen, die mit der  :Bayes-Formel zur Posterior-Dichte                        


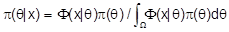
umgeschrieben werden, aus der dann alle Schätzaussagen über q hergeleitet werden. Der Parameter ist hier selbst eine Zufallsvariable. In die dritte Informationsklasse gehören die potentiellen Konsequenzen, die aus der Verwendung der Schätzwerte resultieren und die monetär durch eine Verlustfunktion oder allgemeiner durch eine Nutzenfunktion ausgedrückt werden. Die Verwendung aller drei Arten vorstehender Information führt zu einem entscheidungstheoretischen Schätzansatz.
4. Zu unterscheiden ist  speziell bei Parameterschätzung  zwischen Punkt- und Intervallschätzung. Eine Punktschätzung führt zur Angabe eines Schätzwertes, i.e. einer Zahl, von der man weiß, daß sie allenfalls zufällig mit dem unbekannten Parameterwert übereinstimmen wird. Konstruktionsmethoden für Punktschätzer sind u.a.:          -           Die Momentenmethode, bei der ein Moment der Zufallsvariablen durch das korrespondierende Moment in der Stichprobe geschätzt wird, z.B. m = E(X) durch


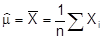
                     (Nach dieser Methode sind auch Funktionsparameter schätzbar, indem man sie durch Momente ausdrückt, für die man dann die Stichprobenmomente einsetzt.)          -           Die Maximum-Likelihood-Methode , bei der die Parameterwerte so gewählt werden, daß die Likelihoodfunktion maximal wird. (Letztere ist die Stichprobendichte oder Stichprobenwahrscheinlichkeit F(x|q), aufgefaßt als Funktion des oder der unbekannten Parameter.)          -           Die Kleinst-Quadrate-Methode, die vornehmlich zur Schätzung der Parameter linearer statistischer Modelle in der Regressionsanalyse Varianzanalyse verwendet wird. Weitere Verfahren sind die c2-Minimum-Methode und  bei Vorliegen geordneter Stichproben  die Methode der Positionsstichproben. Instrumente der Intervallschätzung sind das Konfidenzintervall und das Toleranzintervall. Ein Konfidenzintervall zum Konfidenzniveau 1-a ist in der klassischen Statistik ein in Lage und/od. Breite zufälliger Bereich, der den unbekannten Wert von q mit Wahrscheinlichkeit 1-a überdeckt, und in der Bayes-Statistik ein fester Bereich, der den Anteil 1-a aller Realisationen von q einschließt. Ein Toleranzintervall ist ein Zufallsintervall, in dem mit Wahrscheinlichkeit von mindestens 1-a ein Anteil von wenigstens g aller Realisationen der Zufallsvariablen X enthalten ist, m.a.W. die Wahrscheinlichkeit, mit dem Toleranzintervall eine zukünftige Realisation von X richtig zu prognostizieren, ist mindestens g(1-a).
5. Zur Beurteilung und Auswahl besonders von Parameterschätzverfahren existiert eine Vielzahl von Kriterien:          -           Eine Schätzfunktion


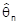
 für q heißt erwartungstreu (unverzerrt), wenn


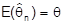
 für alle n. Ansonsten heißt


 verzerrt mit dem Bias


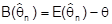
         -           Eine Schätzfunktion heißt (einfach) konsistent, wenn


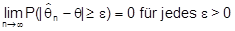
              m.a.W. für erwartungstreue


 gilt das Gesetz der großen Zahlen.          -           Von zwei erwartungstreuen Schätzfunktionen heißt


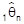
 effizienter als


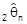
, wenn


 die kleinere Varianz besitzt. Mit der Ungleichung von Rao und Cramér läßt sich unter gewissen Regularitätsvoraussetzungen die Unterschranke der Varianz für die effiziente Schätzung angeben.          -           Eine Schätzfunktion heißt suffizient, wenn sie die gesamte Stichprobeninformation ausschöpft.          -           Eine Schätzfunktion heißt linear, wenn sie eine Linearkombination der Stichprobenvariablen ist.          -           Eine Schätzfunktion heißt (asymptotisch) normal, wenn sie exakt (asymptotisch) normal verteilt ist.          -           Eine Schätzfunktion heißt robust, wenn die Güte der Schätzung auch bei Nichtzutreffen der unterstellten Verteilung im wesentlichen erhalten bleibt.

Literatur: G. Bamberg/F. Baur, Statistik.
7. A., München 1991. R. Deutsch, Estimation Theory, Englewood Cliffs 1965. M. G. Kendall/A. Stuart, The Advanced Theory of Statistics. Vol. 2, 4th ed., London 1979. M. T. Wasan, Parametric Estimation. New York 1970.