|
Kostenbegriffe
Inhaltsübersicht
I. Grundlegende Kostenbegriffe
II. Zweistufige Sichtweise
III. Zusammenfassung
I. Grundlegende Kostenbegriffe
Unter betriebswirtschaftlichen Kosten versteht man den bewerteten sachzielbezogenen Güterverbrauch einer Abrechnungsperiode. Die dieser Definition zugrunde liegende Mengenkomponente bestimmt die zur Leistungserstellung erforderlichen Faktorverbräuche (Ressourcenverbräuche), die über die Wertkomponente vergleichbar gemacht werden. Mengen- und Wertkomponente führen zu unterschiedlichen Präzisierungen des Kostenbegriffs.
1. Wertmäßiger und pagatorischer Kostenbegriff
In Bezug auf die Wertkomponente sind zunächst der wertmäßige und der pagatorische Kostenbegriff zu unterscheiden. Völlig unproblematisch erscheint die Festlegung der Wertkomponente in perfekten Märkten, die dadurch charakterisiert sind, dass jedes zur Produktion erforderliche materielle Gut oder auch jede erforderliche Dienstleistung stets zu einem eindeutigen Marktpreis handelbar ist. Dieser eindeutige Marktpreis stellt dann auch die einzig sinnvolle Bewertung einer zur Produktion erforderlichen Ressource dar.
Während der wertmäßige Kostenbegriff große Freiheitsgrade bei der Gewichtung unterschiedlicher Ressourcenverbräuche zulässt, schreibt der pagatorische Kostenbegriff die Orientierung an Auszahlungen vor. Letzterer orientiert sich damit insbesondere an Anschaffungspreisen. Kalkulatorische Kosten, wie etwa ein kalkulatorischer Unternehmerlohn, werden durch den pagatorischen Kostenbegriff nicht erfasst. Ein weiteres Problem des pagatorischen Kostenbegriffs ist darin zu sehen, dass Anschaffungspreise häufig stark schwanken, was eine Wirtschaftlichkeitskontrolle auf der Basis pagatorischer Kosten erschwert. Ein in die Zukunft gerichteter Ressourceneinsatz sollte nicht davon abhängen, ob in der Vergangenheit, etwa aufgrund einer kurzfristigen Knappheit einer Ressource auf dem Markt, ein außergewöhnlich hoher Anschaffungspreis für die Ressource bezahlt wurde. In der Praxis liegen außerdem für viele der im Rahmen des Wertschöpfungsprozesses einer Unternehmung zu erbringenden Leistungen keine eindeutigen Marktpreise vor. Die Forderung einer Orientierung an Marktpreisen wie beim pagatorischen Kostenbegriff erscheint daher problematisch.
Die Frage nach einem geeigneten Kostenbegriff stellt sich damit offensichtlich immer dann, wenn man von komplexen Entscheidungsfeldern ausgeht, die beispielsweise durch knappe, (kurzfristig) nicht handelbare Produktionsfaktoren charakterisiert sind. Der wertmäßige Kostenbegriff bietet hier die Möglichkeit, Informationen über das zugrunde liegende Entscheidungsfeld zu berücksichtigen. Dabei ist die Idee, Kostenbewertungen zur Lösung konkreter Entscheidungsprobleme heranzuziehen, die durch Entscheidungsmodelle mit spezifischen Präferenzsystemen und Entscheidungsfeldern definiert werden. Das Ziel besteht darin, das Präferenzsystem durch entsprechende Kostenbewertungen so zu modifizieren, dass bestimmte Teile des Entscheidungsfeldes indirekt erfasst werden (vgl. Hax, H. 1967, S. 752 ff.). Die Notwendigkeit, Teile des Entscheidungsfeldes indirekt über das Präferenzsystem abzubilden, ergibt sich natürlich erst dann, wenn das Entscheidungsfeld bei der konkreten Problemlösung nur unvollständig berücksichtigt wird. Zu denken ist hier etwa an eine Restriktion aufgrund einer von mehreren Produkten genutzten Ressource im Rahmen einer Produktionsprogrammplanung. Handelt es sich um eine knappe Ressource, also um einen Engpass, so sind bei einer Vernachlässigung der entsprechenden Restriktion im Entscheidungsfeld positive Opportunitätskosten anzusetzen. Diese Opportunitätskosten sollen die aufgrund der Nutzung der Ressource entgangenen Deckungsbeiträge widerspiegeln. Derartige Opportunitätsüberlegungen lässt der pagatorische Kostenbegriff offensichtlich nicht zu. Er geht damit vielmehr davon aus, dass bei der konkreten Lösung eines Entscheidungsproblems eine genaue Abbildung des zugrunde liegenden Entscheidungsfeldes erfolgt, sodass sich eine indirekte Berücksichtigung von Komponenten des Entscheidungsfeldes in der Zielfunktion erübrigt.
Es lässt sich zeigen, dass, falls eine Berücksichtigung von Teilen des Entscheidungsfeldes über die Zielfunktion möglich ist, die Verwendung des pagatorischen und die des wertmäßigen Kostenbegriffs bei entsprechend angesetzten optimalen Opportunitätskosten zu identischen Lösungen in Bezug auf das zugrunde liegende Entscheidungsproblem, z.B. eine deckungsbeitragsoptimale Produktionsprogrammplanung, führen. In diesem Sinne kann man den pagatorischen Kostenbegriff als den originären und den wertmäßigen als den zugehörigen derivativen Kostenbegriff sehen (vgl. Adam, D. 1970, S. 46). Die Ermittlung optimaler Opportunitätskosten erfordert dabei letztlich die Lösung des entsprechenden Entscheidungsproblems auf Basis pagatorischer Kosten. Es handelt sich damit um einen strukturellen Zusammenhang zwischen pagatorischen und wertmäßigen Kosten, der eine theoretische Rechtfertigung für die Verwendung wertmäßiger Kosten darstellt. Im Rahmen praktischer Anwendungen des wertmäßigen Kostenbegriffs wird es jedoch nur näherungsweise gelingen, optimale Opportunitätskosten anzusetzen.
2. Beispiel
Ein Beispiel (vgl. Kloock, J./Sieben, G./Schildbach, T./Homburg, C. 2005, S. 33 ff.) möge die angestellten Überlegungen verdeutlichen. Es geht um die Produktionsprogrammplanung einer Unternehmung mit zwei Produkten P1 und P2, über deren Produktionsmengen x1 und x2 zu befinden ist. Dabei sollen die folgenden Preis-Absatz-Funktionen gelten:
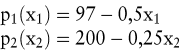
Pro Mengeneinheit fallen für die jeweiligen Produkte Ausgaben in Höhe von k1 = 8 und k2 = 12 an. Außerdem benötigt man zur Produktion der beiden Produkte eine Maschine mit einer Kapazität von 200 Kapazitätseinheiten. Die Produktion einer Mengeneinheit von P1 erfordert 0,5 Kapazitätseinheiten, die von P2 hingegen 1 Kapazitätseinheit. Hieraus erhält man das folgende Totalmodell zur Bestimmung des deckungsbeitragsoptimalen Produktionsprogramms:
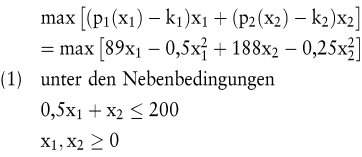
Man geht nun davon aus, dass dieses Modell nicht direkt gelöst wird, sondern eine Zerlegung durchgeführt wird. Zur Bestimmung der optimalen Produktionsmenge für P1 wird das folgende Untermodell gelöst:
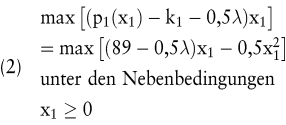
Durch den Parameter λ sollen die Opportunitätskosten für die Nutzung einer Kapazitätseinheit der Maschine berücksichtigt werden. Es erfolgt also gleichsam eine Korrektur des Produktdeckungsbeitrags. Analog erhält man für Produkt P2 das Untermodell:
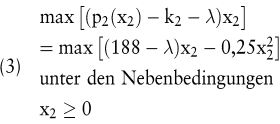
Durch einen Lagrangeansatz für das Totalmodell (1) lassen sich die optimalen Opportunitätskosten λ* ermitteln. Für λ* = 98 erhält man aus den beiden Untermodellen (2) und (3) die Produktionsmengen x1* = 40 und x2* = 180. Diese Produktionsmengen stellen die Optimallösung für das Totalmodell dar.
Mit λ* liegen jedoch auch im Totalmodell x1* und x2* vor, sodass sich die Verwendung von Untermodellen im Prinzip erübrigt. Es wäre jedoch durchaus denkbar, dass man versuchen würde, die anzusetzenden Opportunitätskosten durch ein einfacheres Suchverfahren zu ermitteln. Hierzu könnte man zunächst mit einem beliebigen Wert λ ≥ 0 starten und diesen dann gegebenenfalls verringern oder erhöhen, je nachdem, ob die Maschinenrestriktion (0,5x1 + x2 ≤ 200) im Totalmodell (1) bereits durch die Lösungen der Untermodelle erfüllt wird. Aufgrund von Suchkosten ergibt sich dabei u.U. ein Verfahrensabbruch, bevor man den optimalen Wert λ* = 98 erreicht, sodass man sich mit einem suboptimalen, aber dennoch zulässigen Produktionsprogramm zufrieden gibt. Beendet man das Suchverfahren etwa mit λ = 100, so resultiert das Produktionsprogramm x1 = 39 und x2 = 172. Dies führt zu einer Nutzung der Maschine, die mit 191,5 unter den verfügbaren 200 Kapazitätseinheiten liegt. Es resultiert ein Deckungsbeitrag in Höhe von 27.650,5. Im Gegensatz hierzu wird die Maschinenkapazität bei Verwendung optimaler Opportunitätskosten λ* = 98 durch das optimale Produktionsprogramm x1* = 40 und x2*= 180 voll ausgenutzt, und der optimale Deckungsbeitrag beträgt 28.500.
Ernüchternd hinsichtlich der praktischen Bedeutung des wertmäßigen Kostenbegriffs ist allerdings die Tatsache, dass sich im Rahmen linearer Programme Restriktionen nicht ohne weiteres ersatzweise über Kostenbewertungen in der Zielfunktion berücksichtigen lassen, was eine für die Praxis besonders bedeutende Klasse von Entscheidungsproblemen betrifft. Die Grenzplankostenrechnung als Kostenrechnungssystem für kurzfristige Entscheidungsrechnungen basiert daher auf einer umfassenden Abbildung des zugrunde liegenden Entscheidungsfeldes, die insbesondere über lineare Restriktionen zur Berücksichtigung von Produktionsressourcen erfolgt.
3. Entscheidungsorientierter Kostenbegriff
Wie der pagatorische, so ist auch der entscheidungsorientierte Kostenbegriff im Rahmen der relativen Einzelkostenrechnung von Riebel (vgl. Riebel, P. 1990) streng an Ausgaben (Auszahlungen) orientiert. Dabei dürfen einem Kalkulationsobjekt nur die von der Entscheidung über das Kalkulationsobjekt ausgelösten Ausgaben als Kosten zugerechnet werden. Das insgesamt resultierende Kostenverursachungsprinzip wird als Identitätsprinzip bezeichnet und rechnet einem Kalkulationsobjekt genau die entscheidungsrelevanten Kosten zu. Sämtliche Sunk Costs aufgrund vorgelagerter Entscheidungen, die durch zukünftige Entscheidungen unbeeinflussbar sind, bleiben unberücksichtigt. In Bezug auf die Mengenkomponente wird beim entscheidungsorientierten Kostenbegriff nicht mehr wie beim pagatorischen und beim wertmäßigen Kostenbegriff auf periodenbezogene Güterverbräuche abgehoben. Die Verwendung des entscheidungsorientierten Kostenbegriffs führt daher auch nicht zu einer traditionellen Kostenrechnung, sondern liefert vielmehr ein universell einsetzbares Rechnungssystem zur Bewertung von Entscheidungen.
Kostenrechnungssysteme mit längerfristigem Planungshorizont, wie etwa die Prozesskostenrechnung, verstoßen regelmäßig gegen das Identitätsprinzip, indem sie große Teile des real zugrunde liegenden Entscheidungsfeldes vernachlässigen. So rechnet die Prozesskostenrechnung komplexen Kalkulationsobjekten die Ressourcenkosten fertigungsunterstützender Bereiche gemäß dem Beanspruchungsprinzip zu. Dabei ist jedoch klar, dass die Beanspruchung der Ressourcen indirekter Bereiche nicht in einem unmittelbaren Zusammenhang zu den dort anfallenden Auszahlungen steht. Dennoch wird die (mengenmäßige) Nutzung der entsprechenden Ressourcen mit den Bereitstellungskosten bewertet. Somit werden bewusst vereinfachte Wertansätze gewählt, die als approximative Opportunitätskosten interpretiert werden können und i. Allg. nur zu suboptimalen Entscheidungen führen. Solche suboptimalen Entscheidungen können in der Prozesskostenrechnung beispielsweise die Zusammensetzung des Produktprogramms betreffen.
II. Zweistufige Sichtweise
1. Grundprinzip
Die Verwendung des entscheidungsorientierten Kostenbegriffs erfordert offensichtlich eine sehr genaue Abbildung des Entscheidungsfeldes des zugrunde liegenden Entscheidungsproblems. Insbesondere sind Überlegungen dahingehend notwendig, welche Auszahlungen durch die Entscheidung über ein einziges Kalkulationsobjekt ausgelöst werden. Dies lässt sich nur durch die Berücksichtigung ganzer Entscheidungssequenzen erfassen, wie man sie im Rahmen der flexiblen Planung modelliert. Der entscheidungsorientierte Kostenbegriff ist damit eher als ein theoretischer Idealpunkt zu sehen, an dem andere Kostenbegriffe zu beurteilen sind. So kann etwa eine mit Hilfe des wertmäßigen Kostenbegriffs erzielte Entscheidung anhand eines übergeordneten Entscheidungsmodells unter Verwendung des entscheidungsorientierten Kostenbegriffs bewertet werden (vgl. Schneeweiß, C. 1993, S. 1035 f.).
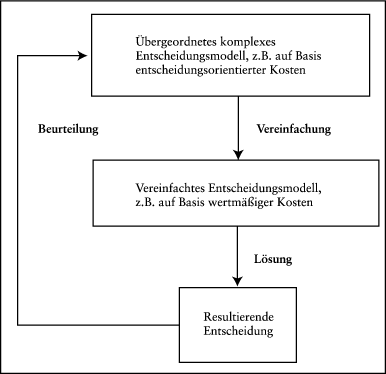
Abb. 1: Grundprinzip einer zweistufigen Vorgehensweise
Abb. 1 verdeutlicht das Grundprinzip einer solch zweistufigen Sichtweise. Ein komplexes Bewertungsmodell dient als (theoretische) Bewertungsebene von Entscheidungen, die mit Hilfe eines vereinfachten Entscheidungsmodells getroffen werden. Die Vereinfachung bezieht sich dabei insbesondere auf die vereinfachte Berücksichtigung des zugrunde liegenden Entscheidungsfeldes, weshalb auf beiden Entscheidungsebenen i. Allg. unterschiedliche Kostenbegriffe verwendet werden. Im Rahmen einer Beurteilung von Entscheidungen, die mit Hilfe vereinfachter Entscheidungsmodelle und unter Verwendung wertmäßiger Kosten generiert werden, spielt es vor allem eine Rolle, ob die wichtigsten Restriktionen des übergeordneten Modells erfüllt sind. Als Beispiel kann hier die Maschinenrestriktion (0,5x1 + x2 ≤ 200) des Totalmodells (1) aus Abschnitt I.2 herangezogen werden. Während das Totalmodell (1) als übergeordnetes Modell fungiert, ergeben sich die vereinfachten Untermodelle (2) und (3) aus einer produktspezifischen Zerlegung dieses Totalmodells, bei der die übergreifende Maschinenrestriktion nur noch über (wertmäßige) Opportunitätskosten berücksichtigt wird. Neben Ressourcenrestriktionen kann es jedoch durchaus auch um die Erfüllung von Mindestansprüchen für bestimmte Ziele gehen. Solche Mindestansprüche sind dann als Restriktionen zu formulieren, deren Einhaltung gegebenenfalls wiederum über den Ansatz von Opportunitätskosten im untergeordneten Modell zu gewährleisten ist.
Eine zweistufige Sichtweise wie in Abb. 1 kann auch zur Erläuterung des investitionstheoretischen Kostenbegriffs (vgl. z.B. Schweitzer, M./Küpper, H.-U. 2003, S. 237 – 267) herangezogen werden. Hier erfolgt eine Präzisierung der Wertkomponente dahingehend, dass man auf der übergeordneten Bewertungsebene von der Maximierung des Kapitalwertes ausgeht. Ziel ist es daher beispielsweise, ein Produktionsprogramm festzulegen, das zu einem kapitalwertmaximalen Zahlungsstrom führt. Ein Zusammenhang zwischen Produktionsprogramm und Zahlungsstrom ergibt sich dabei etwa aufgrund der mit einem Produktionsprogramm einhergehenden Maschinennutzung, die ihrerseits bestimmte Reparatur- und Wartungszahlungen erfordert. Auf der kurzfristigen Produktionsprogrammebene kann der Einfluss auf den längerfristigen Zahlungsstrom nun durch den Ansatz von nutzungsbedingten Abschreibungen für die Maschine erfolgen. Die Höhe der nutzungsbedingten Abschreibungen ist dann möglichst so anzusetzen, dass sie die Veränderung des Kapitalwertkritieriums reflektiert, um ein hinsichtlich dieses übergeordneten Ziels optimales Produktionsprogramm zu erhalten.
Der investitionstheoretische Ansatz berücksichtigt auch im kurzfristigen Bereich sämtliche mit einer Entscheidung verbundenen Zahlungsströme, wozu man sie natürlich zunächst zu prognostizieren hat. Durch die Einordnung in eine zweistufige Sichtweise lässt sich allerdings der Vorwurf entkräften, der investitionstheoretische Ansatz unterliege dem Dilemma der simultanen Planung (vgl. beispielsweise Maltry, H. 1989, S. 89; Schweitzer, M./Küpper, H.-U. 2003, S. 266). Die Interpretation des investitionstheoretischen Ansatzes als Zusammenspiel zwischen einem den langfristigen Zahlungsstrom berücksichtigenden übergeordneten Bewertungsmodell und einem an kurzfristigen Überlegungen ausgerichteten Kostenmodell zeigt, dass es sich letztlich um eine Konkretisierung der Sichtweise in Abb. 1 handelt. Konzeptionell liefert der investitionstheoretische Ansatz dahingehend neue Einsichten, dass er durch seine Spezifikation des übergeordneten Kriteriums als Kapitalwert bzw. allgemeiner als ein mehrperiodiges Kriterium (vgl. Schweitzer, M./Küpper, H.-U. 2003, S. 267) die Notwendigkeit einer Koppelung der kurzfristig orientierten Kostenrechnung mit einem langfristigen Erfolgsziel betont. Die Schwäche des investitionstheoretischen Ansatzes liegt darin, dass er bisher noch nicht auf realistischere Informationssituationen ausgedehnt wurde. Hierzu wäre die Annahme einer idealen Erfassung der untergeordneten Entscheidungsebene aufzugeben, sodass beispielsweise Abschreibungen auf der Grundlage unsicherer Zahlungsströme festzulegen sind.
2. Aspekte der Verhaltenssteuerung
Auf einer übergeordneten Bewertungsebene können aber auch zahlreiche weiter gehende Ziele eine Rolle spielen. Dies trifft gerade bei einer personellen Zerlegung von Entscheidungskompetenzen zu, wie sie typisch ist für dezentrale Unternehmungen. Teilweise müssen hier traditionelle Überlegungen der Kostenrechnung überdacht werden, weil sie nicht mehr auf die theoretisch ermittelten optimalen Kostenwerte führen. Beispielsweise kann die durch Delegation entstehende Informationsasymmetrie zwischen mehreren Entscheidungsträgern dazu führen, dass andere Kostenwerte angesetzt werden müssen als diejenigen, die ein einziger Entscheider im Rahmen einer rein planungsorientierten Kostenrechnung, also ohne Probleme der Verhaltenssteuerung anderer Entscheidungsträger, angesetzt hätte.
Somit bietet eine zweistufige Sichtweise wesentliche Ansatzpunkte zur Beurteilung unterschiedlicher Kostenbegriffe. Dies trifft insbesondere dann zu, wenn zusätzlich davon auszugehen ist, dass Entscheidungsträger ihre sich aus der Informationsasymmetrie ergebenden diskretionären Handlungsspielräume in opportunistischer Weise ausnutzen. Dann sind Kostenwerte i. Allg. unter mehrfachen, konfliktären Zielsetzungen zu beurteilen. Einer Kostenrechnung, die Probleme der Verhaltenssteuerung unter asymmetrischen Informationen und unter konfliktären Zielsetzungen bewältigen will, muss dabei ein äußerst weit gefasster Kostenbegriff zugrunde liegen. Aufgrund von Informationsasymmetrie ist davon auszugehen, dass nicht allen Entscheidungsträgern sämtliche für ihre Entscheidungen relevanten Restriktionen bekannt sind. Selbst in einem Team besteht daher eine zentrale Aufgabe darin, durch geeignete Kostenbewertungen die notwendigen Präferenzanpassungen bei den dezentralen Entscheidungseinheiten zu bewirken. Dies kann etwa durch den Ansatz von (wertmäßigen) Opportunitätskosten geschehen.
Besonders deutlich wird die Notwendigkeit eines flexiblen Kostenbegriffs, wenn mehrere Entscheider im Rahmen von Kommunikationsprozessen miteinander kommunizieren, d.h. Informationen austauschen. Betrachtet man dann auch noch opportunistische Entscheider, so muss mit bewussten Informationsverzerrungen (cheating) gerechnet werden. Beispielsweise können im Rahmen einer Investitionsbudgetierung übertriebene Erfolgsaussichten gemeldet werden, um hohe Investitionsbudgets zu erreichen. Einer allgemein verstandenen Kostenrechnung kommt dann die Aufgabe zu, mit Hilfe geeigneter Kostenbewertungen Anreize zur wahrheitsgemäßen Informationsübermittlung zu schaffen. Die dabei anzusetzenden Kostenbewertungen ergeben sich nicht durch Marktpreise. Vielmehr resultieren sie aus der Verringerung eines übergeordneten monetären Gesamtziels. Kostenbegriffe, die eine derart allgemeine Auslegung zulassen, werden von Schneeweiß und Ewert/Wagenhofer vorgeschlagen. So versteht Schneeweiß unter Kosten Größen, „ die aus tatsächlichen oder erwarteten Auszahlungen abgeleitete Präferenzinformation enthalten und dazu beitragen, zur betrieblichen Leistungserstellung erforderliche Entscheidungen zielgerecht zu treffen “ (Schneeweiß, C. 1993, S. 1031). Ewert/Wagenhofer schlagen eine Kostenkonzeption vor, bei der Kosten die „ Verringerungen der die gegebenenfalls unsicheren, mehrperiodigen monetären Konsequenzen einer Aktion widerspiegelnden Repräsentanzgröße “ (Ewert, R./Wagenhofer, A. 2005, S. 41) darstellen.
In Richtung Verhaltenssteuerung von Entscheidungsträgern gehen auch Überlegungen des Zielkostenmanagements. Hier wird ein Kostenbegriff zugrunde gelegt, bei dem es um die Vorgabe maximal zulässiger Kosten (allowable costs) geht, die aus einer konsequenten Marktorientierung gewonnen werden. Für die Ermittlung der \'allowable costs\' sind dabei der geschätzte Marktpreis und der geplante Produkterfolg maßgebend. Aus der Differenz dieser beiden Größen ergibt sich dann eine entsprechende Kostenvorgabe, an der sich die Mitarbeiter orientieren können. Gegebenenfalls lassen sich aber auch modifizierte, realistischere Vorgaben, etwa im Rahmen partizipativer Aushandlungsprozesse vereinbaren. Im Rahmen einer zweistufigen Sichtweise von Zielkosten wären dann allerdings auf der übergeordneten Bewertungsebene i.Allg. auch Probleme der asymmetrischen Informationsverteilung zu berücksichtigen. Die Informationsasymmetrie bezieht sich dabei insbesondere auf die Potenziale zur Kostenreduktion, über die untergeordnete Mitarbeiter häufig genauere Informationen besitzen als das Topmanagement.
III. Zusammenfassung
Der vorliegende Beitrag sollte zeigen, dass sich unterschiedliche Kostenbegriffe keineswegs ausschließen müssen. Vielmehr ist ihr Zusammenspiel im Rahmen einer zweistufigen Sichtweise mit einer eher theoretischen Bewertungsebene und einer mehr an praktischen Gesichtspunkten orientierten untergeordneten Entscheidungsebene zu analysieren. Gerade wenn bei der übergeordneten Bewertung komplexe Überlegungen der Verhaltenssteuerung anderer Entscheider einfließen, ist auf der übergeordneten Bewertungsebene ein äußerst weit gefasster Kostenbegriff erforderlich.
Literatur:
Adam, Dietrich : Entscheidungsorientierte Kostenbewertung, Wiesbaden 1970
Ewert, Ralf/Wagenhofer, Alfred : Interne Unternehmensrechnung, Berlin et al., 6. A., 2005
Hax, Herbert : Bewertungsprobleme bei der Formulierung von Zielfunktionen für Entscheidungsmodelle, in: ZfbF, Jg. 29, 1967, S. 749 – 761
Kloock, Josef/Sieben, Günter/Schildbach, Thomas/Homburg, Carsten : Kosten- und Leistungsrechnung, Stuttgart, 9. A., 2005
Maltry, Helmut : Plankosten- und Prospektivkostenrechnung, Bergisch Gladbach 1989
Riebel, Paul : Einzelkosten- und Deckungsbeitragsrechnung, Wiesbaden, 6. A., 1990
Schneeweiß, Christoph : Kostenbegriffe aus entscheidungstheoretischer Sicht, in: ZfbF, Jg. 45, H. 12/1993, S. 1025 – 1039
Schweitzer, Marcell/Küpper, Hans-Ulrich : Systeme der Kosten- und Erlösrechnung, München, 8. A., 2003
|