|
Nutzwertanalyse
Inhaltsübersicht
I. Einführung
II. Die Zielgewichtung und ihre Problematik
III. Erweiterungen
I. Einführung
„ Nutzwertanalyse ist die Analyse einer Menge komplexer Handlungsalternativen mit dem Zweck, die Elemente dieser Menge entsprechend den Präferenzen des Entscheidungsträgers bezüglich eines multidimensionalen Zielsystems zu ordnen. Die Abbildung dieser Ordnung erfolgt durch die Angabe der Nutzwerte (Gesamtwerte) der Alternativen. “ Diese Definition von Zangemeister (Zangemeister, C. 1976, S. 45) ist in wörtlicher oder umschreibender Form in der deutschsprachigen betriebswirtschaftlichen Literatur häufig wiederzufinden (vgl. u.a. Bechmann, A. 1982; Bieg, H./Kußmaul, H. 2000, S. 52 ff.; Blohm, H./Lüder, K. 1995, S. 176 ff.; Götze, U./Bloech, J. 1995, S. 133 ff.; Schneeweiß, C. 1991, S. 120 ff.; Weber, M. 1992). Die Menge der Handlungsalternativen wird als gegeben und dem Entscheidungsträger als bekannt unterstellt; sie ist endlich, ihre Elemente werden üblicherweise explizit in einer Tabelle aufgelistet und hier mit H1,..., HN bezeichnet. Der Entscheidende hat, so wird weiter unterstellt, K-dimensionale (mehrdimensionale) Zielvorstellungen bezüglich der gegebenen Alternativen; er ist in der Lage, Zielerreichungsgrade (Zielwerte, Zielerträge, Ausprägungen der Attribute, ?) znk für seine K Ziele (Kriterien, Attribute, Merkmale) für alle Alternativen zu artikulieren (n = 1, ..., N; k = 1, ..., K). Die Zielerreichungsgrade können sowohl reelle Zahlen als auch verbale Artikulierungen des Entscheidungsträgers sein, die Vorstellungen zum Vergleich zweier Alternativen beinhalten. Da von endlich vielen Alternativen und von endlichen vielen Zielen ausgegangen wird, kann das zu analysierende Entscheidungsproblem in einer Tabelle dargestellt werden.
Wenn hier von einer Tabelle – und nicht von einer Matrix – gesprochen wird, dann um zu betonen, dass es sich bei den Elementen dieser Tabelle nicht notwendig um reelle Zahlen handeln muss. Um mithilfe seiner Zielerreichungsgrade zu einer Entscheidung zu gelangen, sollte der Entscheidungsträger seine subjektiven Präferenzen dadurch zum Ausdruck bringen, dass er seine Zielerreichungsgrade in vergleichbare Nutzenwerte (Nutzwerte, Teilnutzen, Nutzenpunkte, Scores, ?) unk mit einheitlicher Dimension transformiert und damit vergleichbar macht (n = 1,..., N; k = 1,..., K). Es ist nicht ausgeschlossen, dass Zielerreichungsgrade und Nutzenwerte ganz oder teilweise übereinstimmen.
Da sinnvollerweise davon auszugehen ist, dass der Idealzielpunkt (utopia point) nicht erreichbar ist, d.h. keine zulässige Alternative existiert, die für alle Ziele eine individuell optimale Lösung darstellt, liegt ein Zielkonflikt vor. Die Nutzwertanalyse ist somit als ein spezielles Entscheidungsunterstützungssystem der multikriteriellen Entscheidungstheorie zu sehen, die ihrerseits zahlreiche Kompromissmodelle (Aggregationsmodelle) zur Lösung von Zielkonflikten erarbeitet und deren Implikationen analysiert hat. Eine umfangreiche, recht allgemeine Klasse von Kompromissmodellen basiert auf Abstandsfunktionen, mit deren Hilfe eine zulässige Kompromisslösung gefunden werden kann, die einen bestimmten Abstand etwa vom unzulässigen Idealzielpunkt minimiert (vgl. Dinkelbach, W./Kleine, A. 1996, S. 52 ff.). Zu dieser Klasse gehört auch das für die Grundlagen der Nutzwertanalyse zentrale Zielgewichtungsmodell (additives Modell, lineares Modell).
II. Die Zielgewichtung und ihre Problematik
Die Zielgewichtung zur Lösung von Zielkonflikten wird in der Betriebswirtschaftslehre seit langem diskutiert (vgl. u.a. Heinen, E. 1966, S. 142 ff.; Strebel, H. 1972). Es werden für alle Alternativen die einzelnen Zielfunktionen, hier die Nutzenwerte, mit vom Entscheidungsträger zu wählenden positiven Gewichten g1,..., gK multipliziert und anschließend addiert. Sodann ist die so gebildete Summe Ψn bezüglich n zu maximieren:
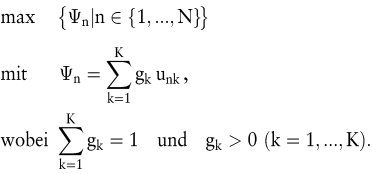
Bei diesem Vorgehen ist garantiert, dass eine so gefundene optimale Lösung effizient bezüglich des vorliegenden Entscheidungsproblems ist, d.h., dass keine andere zulässige Alternative existiert, die in wenigstens einem Ziel zu einem besseren und bei keinem Ziel zu einem schlechteren Ergebnis führt.
Hat der Entscheidungsträger eine optimale Lösung gefunden, dann kann gegebenenfalls die Frage nach dem Bereich entstehen, in dem die Gewichte (Gewichtsvektoren) variieren können, ohne dass die gefundene Lösung ihre Optimalität in Bezug auf die gewählten Gewichte verliert. Anhand der Ergebnisse einer derartigen Sensitivitätsanalyse kann sich der Entscheidende in seiner Wahl der Gewichte bestätigt fühlen oder nicht. – Ist der Entscheidungsträger nicht geneigt, seine Gewichte von vornherein festzulegen, ist es nahe liegend, das Kompromissmodell entweder für mehrere Gewichtsvektoren oder gar für alle zulässigen Gewichte zu lösen. Auch auf diese Weise können dem Entscheidungsträger die Konsequenzen einer Gewichtung transparent gemacht werden, sodass es ihm anschließend leichter fällt, die endgültige Wahl der Gewichte zu treffen (vgl. u.a. Dinkelbach, W. 1982, S. 182 ff.; Zangemeister, C./Bomsdorf, E. 1983). – Auf eine axiomatische Fundierung der Nutzwertanalyse kann an dieser Stelle nicht eingegangen werden (vgl. u.a. Lillich, L. 1992; Eisenführ, F./Weber, M. 1999, S. 115 ff.).
1. Beispiel (Zwei-Ziele-Fall)
Die international aufstrebende Universität des Sparlandes ist in der Lage, einen dringend benötigten Hörsaal mittlerer Größe zu bauen. Die zuständige Baukommission hat bereits fünf Angebote eingeholt, die den vorgegebenen baulichen Rahmenbedingungen entsprechen, sich jedoch bezüglich dreier Kriterien unterscheiden, die noch gegeneinander abzuwägen sind. Es handelt sich (1.) um die Anzahl der Sitzplätze, (2.) um die mehr oder weniger komfortable technische Ausstattung sowie (3.) um unter ökologischen Aspekten unterschiedliche Klimaanlagen, auf deren Berücksichtigung an dieser Stelle zunächst verzichtet wird.
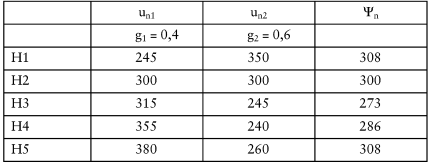
Tab. 1: Entscheidungsmatrix für den Zwei-Ziele-Fall
Die Konkretisierung der beiden ersten Ziele ist relativ trivial. Die jeweiligen Zielwerte können, so wird unterstellt, der Objektbeschreibung unmittelbar entnommen werden. Die Anzahl der Sitzplätze als erstes zu maximierendes Ziel kann unmittelbar als Nutzenwert interpretiert und der zweiten Spalte der Tab. 1 entnommen werden. Entsprechendes gilt für die technische Ausstattung als zweites zu maximierendes Ziel. Die Höhe der Nutzenwerte in der dritten Spalte der Tab. 1 entspricht 1/1000 der jeweiligen Gesamtbeschaffungsausgaben. Bereits ein flüchtiger Blick auf die Entscheidungsmatrix zeigt, dass die beiden Ziele konfliktär sind: Der Hörsaal H5 ist individuelles Optimum des ersten Ziels, der Hörsaal H1 individuelles Optimum des zweiten Ziels (vgl. Tab. 1).
Die Baukommission hatte sich bereits vorab auf eine Gewichtung g1 = 0,4 und g2 = 0,6 geeinigt. Damit lautet die Kompromisszielfunktion:
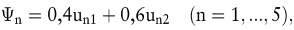
,
deren Werte in der letzten Spalte der Tab. 1 aufgelistet sind. Zur Überraschung der Mitglieder der Kommission sind die bezüglich der zwei Ziele so unterschiedlichen Hörsäle H1 und H5 beide bezüglich der Zielgewichtung als Kompromissmodell optimal (vgl. die Gerade <$>displaystyle Psi_n<$> = 308 durch die Punkte H1 und H5 in Abb. 1). M.a.W.: Die Nutzwertanalyse führt nicht zwingend zu einer eindeutigen Lösung des vorliegenden Entscheidungsproblems.
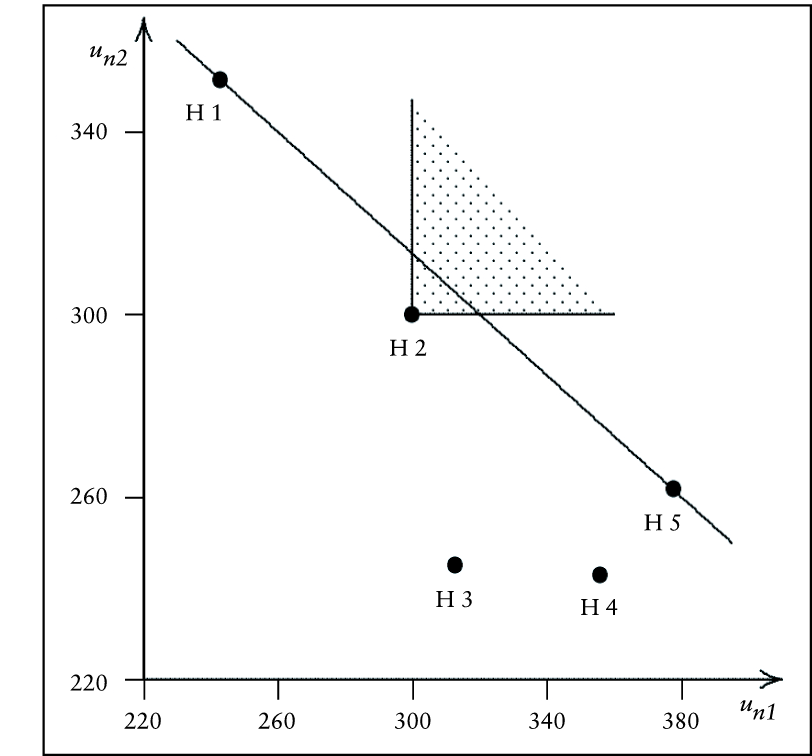
Abb. 1: Alternativenmenge im (un1, un2)-Diagramm
Eine weitere Analyse des Entscheidungsproblems führt zu folgendem Ergebnis: Der bezüglich der Zielgewichtung nicht optimale Hörsaal H2 wird von keinem anderen Hörsaal dominiert, er ist effizient bezüglich des vorliegenden Entscheidungsproblems (vgl. den in Abb. 1 angedeuteten Dominanzkegel für H2). Dieses Problem wird im Rahmen der Nutzwertanalyse weitgehend vernachlässigt. Könnte nicht der Hörsaal H2 ein sinnvoller Kompromiss zwischen den Hörsälen H1 und H5 sein? – Die nicht optimalen Hörsäle H3 und H4 werden vom Hörsaal H5 dominiert, der bei beiden Zielen für alle Gewichtungskombinationen einen höheren Wert aufweist (vgl. Tab. 1 und Abb. 2). Die Abb. 2 verdeutlicht auch, dass in diesem Beispiel für 0 ≤ g2 < 0,6 bzw. 0,4 < g1 ≤ 1 der Hörsaal H5, für 0,6 < g2 ≤ 1 bzw. 0 ≤ g1 < 0,4 der Hörsaal H1 und für g1 = 0,4 bzw. g2 = 0,6 sowohl H1 als auch H5 optimal sind. Die Frage, ob auch weitere Kompromissmodelle, die nicht von vornherein effiziente Alternativen – wie hier die Alternative H2 – als mögliche optimale Lösungen ausschließen, hinzugenommen werden sollen, wird nicht diskutiert (vgl. Dinkelbach, W./Kleine, A. 2001).
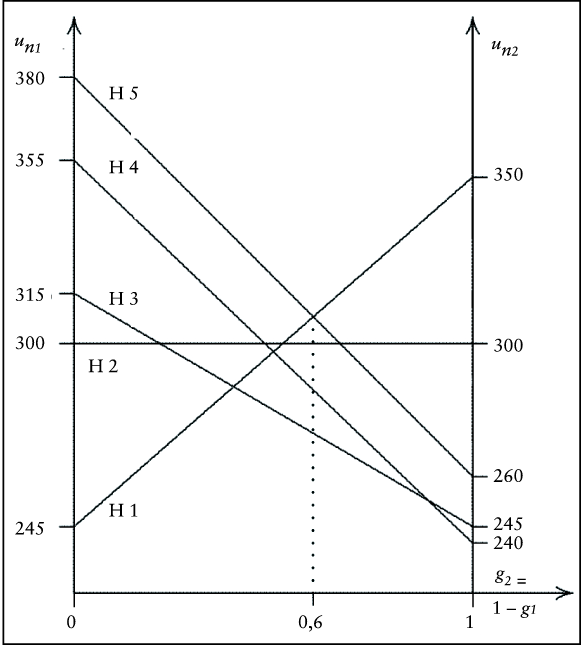
Abb. 2: Grafischer Alternativenvergleich
2. Beispiel (Drei-Ziele-Fall)
Als sich kein Kompromiss anbahnt, schlägt der Umweltbeauftragte vor, die Umweltverträglichkeiten der Klimaanlagen in den Entscheidungsprozess einzubeziehen, etwa in Hinblick auf deren Energieverbrauch und Schadstoffemissionen. Die Hörsäle H1, H2 und H5 werden von den Teilnehmern als befriedigend, der Hörsaal H4 als gut und der Hörsaal H3 als sehr gut eingestuft, jeweils mit den Nutzenwerten 300, 400 bzw. 600 (vgl. Tab. 2).
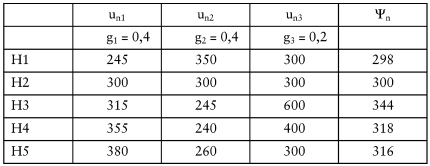
Tab. 2: Entscheidungsmatrix für den Drei-Ziele-Fall
Eine vertiefte Analyse des erweiterten Entscheidungsproblems zeigt die Abb. 3, in der für alle Kombinationen der Gewichte, d.h. für g1 + g2 + g3 = 1 mit g1, g2, g3 ≥ 0, der jeweils optimale Hörsaal bzw. die jeweils optimalen Hörsäle veranschaulicht werden. Auf Drängen der Sitzungsleiterin entscheidet sich die Baukommission für g1 = g2 = 0,4 und g3 = 0,2. Damit ist der Hörsaal H3, also jener, der im Zwei-Ziele-Fall dominiert wurde, optimale Lösung bezüglich einer Zielgewichtung mit den genannten Gewichten (vgl. Punkt * in Abb. 3). Im Übrigen erhält der Hörsaal H1, der im Zwei-Ziele-Fall optimale Lösung war, nunmehr den schlechtesten Kompromisswert (Nutzwert).
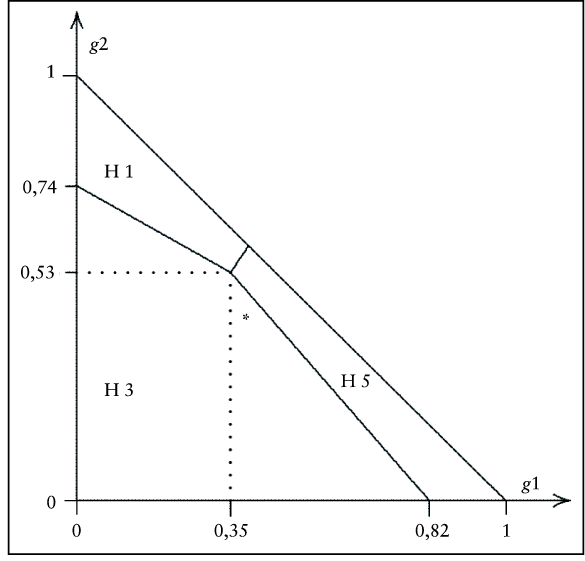
Abb. 3: Grafische Lösung für alle zulässigen Gewichte
Die Ergebnisse einer Nutzwertanalyse sind in hohem Maße, wie das Beispiel gezeigt hat, subjektiv und zugleich sensitiv, selbst dann, wenn die Durchführung der Analyse bei oberflächlicher Betrachtung eine nicht gegebene Objektivität vortäuscht. Aus diesem Grunde sind die hier beispielhaft vorgeführten Sensitivitätsanalysen von zentraler Bedeutung.
III. Erweiterungen
Neben der hier beschriebenen Nutzwertanalyse, die auch als Nutzwertanalyse im engeren Sinne bezeichnet wird, gibt es zahlreiche Varianten. So verzichtet die so genannte Nutzwertanalyse der zweiten Generation etwa auf Einführung reellwertiger (kardinaler) Nutzenwerte und beschränkt sich beim Vergleich von Alternativen auf ordinale Skalen (vgl. Bechmann, A. 1982). Andere Ansätze der Nutzwertanalyse greifen auf Methoden der Fuzzy-Logik zurück und beurteilen Ziele bzw. deren Zielerreichungsgrade mithilfe von Zugehörigkeitsfunktionen, die mittels geeigneter Regeln bzw. Operatoren zu aggregieren sind (vgl. Figge, F. 2000, S. 111 ff.).
Auf die multiattributive Nutzentheorie (Multiattributive Decision Making) gehen insbesondere axiomatisch begründete Erweiterungen der Nutzwertanalyse zurück. Neben der additiven Aggregation der kardinalen Nutzenwerte wird beispielsweise eine Multiplikation oder multilineare gewichtete Verknüpfung entsprechender Nutzenwerte vorgeschlagen (vgl. von Nitzsch,, R. 1992, S. 47 ff.). Diese Varianten ermöglichen die Berücksichtigung von Abhängigkeiten zwischen unterschiedlichen Zielen. Während bei diesen Varianten Interaktionen zwischen den Zielen vom jeweiligen Nutzenniveau abhängen, erlauben Erweiterungen auf der Grundlage nichtadditiver Gewichtungen die Einbeziehung von generellen Abhängigkeiten zwischen Zielen. Diese Verfahren basieren auf einer Gewichtung von Zielen bzw. von Zielpaaren, die sich als Fuzzy Measure interpretieren lassen, sodass eine nutzenmaximale Alternative unter Verwendung eines Choquet-Integrals bestimmt werden kann (vgl. Grabisch, M. 1996; Grabisch, M./Roubens, M. 2000).
Literatur:
Bechmann, Armin : Nutzwertanalyse, in: HdWW, Bd. 9, hrsg. v. Albers, Williet al., Stuttgart 1982, Sp. 799 – 812
Bieg, Hartmut/Kußmaul, Heinz : Investitions- und Finanzierungsmanagement, Bd. I: Investition, München 2000
Blohm, Hans/Lüder, Klaus : Investition, München, 8. A., 1995
Dinkelbach, Werner : Entscheidungsmodelle, Berlin et al. 1982
Dinkelbach, Werner/Kleine, Andreas : Elemente einer betriebswirtschaftlichen Entscheidungslehre, Berlin et al. 1996
Dinkelbach, Werner/Kleine, Andreas : Produktionscontrolling – Effiziente Produktionen in diskreten Technologien, in: ZfB, Jg. 71, Ergänzungsheft 2/2001, S. 51 – 80
Eisenführ, Franz/Weber, Martin : Rationales Entscheiden, Berlin et al., 3. A., 1999
Figge, Frank : Öko-Rating, Berlin et al. 2000
Götze, Uwe/Bloech, Jürgen : Investitionsrechnung, Berlin et al., 2. A., 1995
Grabisch, Michel : The Application of Fuzzy Integrals in Multicriteria Decision Making, in: European Journal of Operational Research, 1996, Bd. 89, S. 445 – 456
Grabisch, Michel/Roubens, Marc : Application of the Choquet Integral in Multicriteria Decision Making, in: Fuzzy Measures and Integrals, hrsg. v. Grabisch, Michel et al., Heidelberg 2000, S. 348 – 374
Heinen, Edmund : Das Zielsystem der Unternehmung, Wiesbaden 1966
Lillich, Lothar : Nutzwertverfahren, Heidelberg 1992
Schneeweiß, Christoph : Planung 1: Systemanalytische und entscheidungstheoretische Grundlagen, Berlin et al. 1991
Strebel, Heinz : Zur Gewichtung von Urteilskriterien bei mehrdimensionalen Zielsystemen, in: ZfB, Jg. 42, 1972, S. 89 – 128
von Nitzsch, Rüdiger : Entscheidungen bei Zielkonflikten, Wiesbaden 1992
Weber, Martin : Nutzwertanalyse, in: HWO, hrsg. v. Frese, Erich, Stuttgart, 3. A., 1992, Sp. 1435 – 1448
Zangemeister, Christof : Nutzwertanalyse in der Systemtechnik, München, 4. A., 1976
Zangemeister, Christof/Bomsdorf, Eckart : Empfindlichkeitsuntersuchungen in der Nutzwertanalyse (NWA): Ermittlung kritischer Zielgewichte und Empfindlichkeitsmaße, in: ZfBF, Jg. 35, 1983, S. 375 – 397
|