|
Investitionsrechnung
Auch: Wirtschaftlichkeitsrechnung. Gesamtheit - und jedes einzelne der Verfahren -der Rentabilitätsberechnungen von geplanten oder realisierten Investitionen auf der Basis quantitativer Grössen. Wichtiges Instrument zur Vorbereitung und Unterstützung von Investitionsentscheidungen. Für die Kreditwürdigkeitsprüfung der um Investitionskredit angegangenen Bank ist eine sorgfältige, überprüfbare, auf realistischen Annahmen beruhende Investitionsrechnung des Kredit suchenden Unternehmens wichtige Beurteilungsunterlage.
1. Begriff. Mit dem Ausdruck I. bezeichnet man die Summe aller Verfahren zur Beurteilung der quantifizierbaren Konsequenzen von Investitionen. Daraus folgt, daß sich die I. immer an quantitativen (= monetären) Zielen orientieren muß. Der I. kommt somit im Rahmen der Investitionsplanung nur eine Teilaufgabe zu, denn die endgültige Investitionsentscheidung muß selbstverständlich auch nicht quantifizierbare Folgen von Investitionen berücksichtigen.
2. Aufgabe. Die I. kommt sowohl in der Entscheidungs- als auch in der Kontrollphase der Investitionsplanung zum Einsatz. In der Entscheidungsphase (= ex ante-Rechnung) dient die I. zur quantitativen Bewertung mehrerer Investitionsmöglichkeiten entsprechend ihrem Beitrag zur Zielrealisierung des Investors. In der Kontrollphase (= ex post-Rechnung) erfolgt sodann der Vergleich der tatsächlich eingetretenen Entwicklung mit den ursprünglichen Plangrößen, um den rechtzeitigen Einsatz evtl. notwendiger Korrekturmaßnahmen sicherzustellen. Als in Frage kommende quantitative Größen zur Beurteilung eines Investitionsprojektes sind insbesondere die Begriffspaare Einzahlungen/Auszahlungen, Einnahmen / Ausgaben , Ertrag / Aufwand und Leistung / Kosten zu nennen. In der Praxis sowie in der Fachliteratur erfolgt die Anknüpfung zumeist an Einzahlungen/Auszahlungen, d.h. an Zahlungsgrößen.
3. Arten. Je nach Unterscheidungskriterium lassen sich die I.-sverfahren in verschiedene Kategorien einteilen: nach der Berücksichtigung des Faktors Zeit (statische/dynamische Verfahren (statische Analyse, dynamische Analyse)), nach der Art der Investitionsentscheidung (Beurteilung eines einzelnen Investitionsprojekts/Investitionsprogrammplanung), nach der Sicherheit der Erwartung (sichere/unsichere Erwartung).
3. 1. Statische/dynamische Verfahren. Die Verfahren zur Beurteilung eines einzelnen Investitionsprojektes lassen sich unter dem Aspekt der Berücksichtigung des zeitlichen Faktors in statische und dynamische Verfahren gliedern. Die dynamischen Methoden unterziehen die Investition einer Totalbetrachtung, d.h. es finden die Ein- und Auszahlungen in allen zukünftigen Perioden bis zum Ende der Planungs- bzw. Nutzungsdauer Eingang in die Rechnung, wohingegen die statischen Modelle sich auf eine einzige (die erste oder eine Durchschnitts-) Periode beziehen. An statischen Verfahren sind insbesondere die Kostenvergleichsrechnung, die Gewinnvergleichsrechnung, die Rentabilitätsrechnung (Rentabilität) und die Amortisationsrechnung (Amortisation) zu nennen. Bei der Kostenvergleichsrechnung werden aus Gründen der Schätzgenauigkeit zumeist die Kosten der ersten Periode (gegliedert in Kapital- und Betriebskosten) als Entscheidungskriterium herangezogen. Bei der Gewinnvergleichsrechnung bildet der durch die Investition durchschnittlich erzielte Gewinn pro Periode den Beurteilungsmaßstab. Die Rentabilitätsrechnung ermöglicht hingegen Aussagen über die absolute Vorteilhaftigkeit eines Projekts. Maßgeblich ist hier die Rentabilität, ausgedrückt als durchschnittlicher Periodengewinn in Prozent des durchschnittlichen Kapitaleinsatzes. Die Vorteilhaftigkeit eines Projektes gilt dann als gegeben, wenn dieser Prozentsatz eine vorgegebene Mindestverzinsung übersteigt. Auch hier wird oft mit dem Gewinn der ersten Periode anstatt eines durchschnittlichen Gewinns gerechnet. Bei der Amortisationsrechnung (Pay-off-Rechnung) wird als Beurteilungsmaßstab kein Geldbetrag oder Prozentsatz, sondern ein Zeitraum herangezogen. Es wird jene Zeitspanne ermittelt, nach der das eingesetzte Kapital wieder zurückgewonnen werden kann (= Wiedergewinnungszeit, Amortisationszeit). Diese Zeit ergibt sich durch Division des Kapitaleinsatzes durch den durchschnittlichen Rückfluß pro Periode. Das Projekt gilt als vorteilhaft, wenn dieser Zeitraum kürzer als eine vorgegebene Frist ist. Dynamische Verfahren sind die Kapitalwertmethode, die Methode des internen Zinsfußes und die Annuitätenmethode. Bei der Kapitalwertmethode (Kapitalwert) wird der Barwert aller zukünftigen Ein- und Auszahlungen (evtl. einschließlich Liquidationserlös (Liquidation)) der Anfangsauszahlung gegenübergestellt. Die in der Zukunft anfallenden Zahlungen werden mit dem Kalkulationszinsfuß diskontiert (Abzinsung) und solchermaßen vergleichbar gemacht:
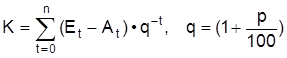
n = Anzahl der Nutzungsperioden, p = Kalkulationszinsfuß, Et = Einzahlungen der Periode t, At = Auszahlungen der Periode t. Das Investitionsprojekt gilt als vorteilhaft, wenn sein Kapitalwert (K) größer oder gleich Null ist, der Kapitalwert ist dann der über die Amortisation und Verzinsung des eingesetzen Kapitals hinaus erwirtschaftete Betrag. Bei der Methode des internen Zinsfußes dient zunächst die Formel der Kapitalwertmethode als Ausgangspunkt: der interne Zinsfuß (Zins) ist jener Kalkulationszinsfuß, für den der Kapitalwert einer gegebenen Einzahlungs-/Auszahlungsreihe gleich Null wird. Der daraus ermittelte interne Zinsfuß reflektiert die Verzinsung des gebundenen Kapitals. Das Investitionsprojekt ist vorteilhaft, wenn dieser Wert eine vorgegebene Mindestverzinsung übersteigt. Problematisch gestaltet sich die praktische Berechnung, da hierzu eine Gleichung n-ten Grades, mit n = Nutzungsdauer des Projektes, zu lösen ist. Deshalb ist der interne Zinsfuß für n ³ 4 nur annäherungsweise, für bestimmte Einzahlungs-/Auszahlungsreihen nicht eindeutig oder gar nicht bestimmbar. Aus diesen Gründen gilt dieses Verfahren als theoretisch unhaltbar, wenngleich es sich in der Praxis großer Beliebtheit erfreut. Das Entscheidungskriterium der Annuitätenmethode ist die Annuität, das ist das Produkt aus Kapitalwert (K) und Annuitätenfaktor. Ist die Annuität größer oder gleich Null, so gilt die Investition als vorteilhaft. Die Annuität (A) gibt dann die Höhe des durchschnittlichen Periodenüberschusses an:
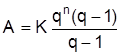
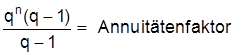
Sowohl statische als auch dynamische Komponenten weist die sogenannte MAPI-Methode auf. Ihr etwas eingeschränkter Anwendungsbereich ist der Ersatz einer bestehenden durch eine neue Anlage. Es soll ermittelt werden, ob diese Ersatzinvestition (Investition) sofort oder erst nach Ablauf eines Jahres erfolgen soll. Beurteilungsmaßstab ist die MAPI-Rentabilitätszahl:
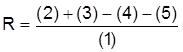
R...... Rentabilitätszahl
(1) .... Nettoinvestitionssumme der neuen Anlage
(2) .... Rohüberschuß der nächsten Periode
(3) .... vermiedener Kapitalverzehr der nächsten Periode
(4) .... Kapitalverzehr der neuen Anlage in der nächsten Periode
(5) .... Ertragsteuern auf den zusätzlichen Gewinn. Bei der Ermittlung des Kapitalverzehrs der neuen Anlage kommen zur Vereinfachung spezielle Diagramme zum Einsatz. Da der Anwendung dieses Verfahrens jedoch recht einschränkende Ausgangsbedingungen zugrundeliegen (Ertragsteuersatz von 50%, Verzinsung des Eigen - und Fremdkapitals sowie Verschuldungsgrad entsprechend amerikanischen Verhältnissen), ist sein Einsatz in der Praxis nicht immer gerechtfertigt.
3. 2. Einzelprojekt-/Investitionsprogrammplanung. Bei der Beurteilung eines einzelnen Investitionsprojektes ist entweder zu entscheiden, ob eine konkrete Investition durchgeführt werden soll oder aber es ist eine bestimmte Investition aus einer Reihe verschiedener, einander ausschließender Investitionsmöglichkeiten zu wählen. Hierbei wird von Interdependenzen zwischen einzelnen Investitionen abstrahiert. Die Rechenverfahren zur Beurteilung einzelner Investitionsprojekte lassen sich ihrerseits in die beiden großen Gruppen der statischen und dynamischen I.-sverfahren (siehe oben) untergliedern. Zur Planung eines Investitionsprogramms hingegen bedient man sich anderer Methoden. Die I.-sarten zur Investitionsprogrammplanung werden in die sukzessiven (klassischen) und die simultanen (Operations Research-Verfahren) eingeteilt. Die Ermittlung des Investitionsprogramms nach der sukzessiven Methode erfordert zunächst eine Einteilung der Einzelinvestitionen in notwendige Investitionen, das sind solche, die unabhängig von ihrer Wirtschaftlichkeit durchgeführt werden müssen, und solche Investitionen, die nicht unbedingt erforderlich, d.h. einer Wirtschaftlichkeitsbetrachtung zu unterwerfen sind. Diese nicht unbedingt notwendigen Investitionsprojekte werden sodann in eine Rangreihe gebracht, wobei das anzuwendende Ordnungskriterium einem dynamischen I.-sverfahren entstammt (z.B. interner Zinsfuß oder Kapitalwertrate, d.h. Verhältnis Kapitalwert/Kapitaleinsatz). In dieser Reihenfolge werden sodann die einzelnen Investitionsprojekte ins Programm aufgenommen, bis entweder die beschränkten Finanzmittel erschöpft oder z.B. der interne Zinsfuß des betrachteten Investitionsprojekts kleiner als der Zinsfuß für die erforderlichen Finanzierungsmittel ist. Bei Vorliegen variabler Zinssätze für das beschränkte Kapitalangebot ist der Schnittpunkt der Kapitalangebots- und der Kapitalnachfragefunktion für die Bestimmung des optimalen Investitionsprogramms maßgeblich. Die Operations Research-Verfahren, auch kombinatorische Verfahren genannt, betrachten jeweils simultan Investitions- und Produktionsprogramm oder Investitions- und Finanzierungsprogramm, wobei das Finanzierungs- bzw. Produktionsprogramm in Form von Restriktionen in die Modelle Eingang findet. Diese Betrachtungen erstrecken sich entweder über eine (Einperioden-) oder mehrere Perioden (Mehrperiodenmodelle), wobei letztere den Vorzug besitzen, zeitlich vertikale Abhängigkeiten verschiedener Investitionsprojekte darstellen zu können. Als Entscheidungskriterium werden der Kapitalwert (= Anfangswert), der Endwert oder eine feste jährliche Entnahme herangezogen. Das Lösungsverfahren besteht in der (ganzzahligen) linearen Optimierung, wobei bis heute allerdings bei der Anzahl der Variablen und Nebenbedingungen kaum praxisrelevante Größenordnungen erreicht werden.
3. 3. Besondere Probleme. Die besonderen Probleme der I. bestehen speziell in den Bereichen der Zurechnung der Ein- und Auszahlungen auf einzelne Investitionsprojekte als auch in der Datenunsicherheit. Das Zurechnungsproblem tritt besonders bei mehrstufigen Produktionsprozessen oder dem Vorliegen zeitlicher (horizontaler oder vertikaler) Interdependenzen auf. Das Problem der Datenunsicherheit liegt prinzipiell nicht nur der I., sondern jeder Form der Planungsrechnung zugrunde. Die Ansätze zur Berücksichtigung der Unsicherheit in den einzelnen Verfahren gehen verschiedene Wege: Durch Zuschläge zu den Auszahlungen und zum Kalkulationszinsfuß sowie Abschläge von den Einzahlungen und der Nutzungsdauer kann die Datenunsicherheit, wenn auch nur pauschal, erfaßt werden (Korrekturverfahren). Im Rahmen der Sensitivitätsanalyse wird die Beeinflussung des Rechenergebnisses (= des Entscheidungskriteriums) durch Datenänderungen untersucht. Zu unterscheiden sind dabei die lokale Sensitivitätsanalyse, bei der jener Bereich festgestellt wird, in dem die Daten schwanken dürfen, ohne daß sich die Beurteilung des Investitionsprojekts ändert, und die globale Sensitivitätsanalyse, bei der der Bereich der Datenschwankungen festgesetzt wird und seine Auswirkungen untersucht werden sollen. Einzelne Kenngrößen, die als Entscheidungskriterium gelten, können auch durch ihre Wahrscheinlichkeitsverteilungen ersetzt werden. Ihr Erwartungswert bzw. ihre Standardabweichung gelten dann als neue Beurteilungskriterien. Diese Methode wird Risikoanalyse genannt. Abschließend sei festgestellt, daß die I. nur einen Teilbereich betrieblicher Planung erfaßt. Nur ihr Zusammenwirken mit anderen Teilplänen, insbesondere im Bereich Finanzierung , Produktion und Absatz , bildet das Fundament verantwortungsbewußter betrieblicher Leitung und Kontrolle.
Literatur: H. Blohm/K. Lüder, Investition. München 1991. H. Heinhold, Arbeitsbuch zur Investitionsrechnung. München 1989. L. Kruschwitz, Investitionsrechnung. Berlin New York 1993.
|