Produktionstheorie

beschäftigt sich mit Konzepten der systematischen Beschreibung von technischen Produktionsmöglichkeiten, die in einer Wirtschaftseinheit (z.B. in einem Teilbereich oder Gesamtbereich eines Betriebes, in einer Gruppe von Betrieben oder in einer Volkswirtschaft) bestehen.  Die Beschreibung ist auf den Informationsbedarf von Ökonomen abgestimmt. Diese benötigen in den meisten Fällen zur Lösung ihrer Probleme kein Handbuch der Verfahrenstechnik, sondern einfachere und aggregiertere Darstellungen, die sich im Rahmen von ökonomischen Modellanalysen und Kalkulationen ohne Schwierigkeiten als integrierter Teilbereich verwenden lassen, Kostentheorie und Unternehmenstheorie . Unter Produktion wird die Transformation von Gütern und Dienstleistungen in andere Güter und Dienstleistungen im Rahmen einer Wirtschaftseinheit verstanden. Die dabei verbrauchten oder gebrauchten Güter und Dienstleistungen heißen Produktionsfaktoren , die entstehenden Güter und Dienstleistungen Produkte .  Ein Produktionspunkt gibt die in einem Produktionsprozeß verbrauchten bzw. gebrauchten Produktionsfaktormengen und die anfallenden Produktmengen an.  Die Gesamtheit der in einer Wirtschaftseinheit alternativ oder kombiniert möglichen Produktionspunkte wird als Technologie der Wirtschaftseinheit bezeichnet.  Ein Produktionspunkt wird üblicherweise in Form eines Vektors in folgender Weise geschrieben: (O1(i), ..., On(i), -v1(i), ..., -vm(i)). Der obere Index (i) kennzeichnet die laufende Nummer des Produktionspunktes. O1(i)  ist die Menge des Produktes der Produktart 1,O2(i)  die Menge des Produktes der Produktart 2 usw.V1(i) ist die Menge des Produktionsfaktors der Art 1,V2(i) die Menge des Produktionsfaktors der Art 2 usw. Der Produktionspunkt i ist genau dann technisch effizient, wenn die Wirtschaftseinheit über keinen anderen Produktionspunkt  nachfolgend Produktionspunkt s genannt  verfügt, der die Ungleichung  (O1(s),..., On(s),...,  -V1(s),..., .-Vm(s))  ³ (O1(i),...,-V(i),...,-Vm (i)) erfüllt.Darstellungen der Technologie einer Wirtschaftseinheit beschränken sich deshalb auf eine Darstellung der technisch effizienten Produktionspunkte, weil technisch ineffiziente Produktionspunkte bei jeder denkbaren Preiskonstellation ökonomisch unterlegen sind. Potentieller technischer Fortschritt findet in einer Wirtschaftseinheit statt, wenn deren Technologie durch einen neuen technisch effizienten Produktionspunkt erweitert wird. Die zeitliche Dimension des Produktionspunktes ist die Produktionsperiode, d.h. der Zeitraum, in dem die Faktoreinsätze und Produkterstellungen erfolgen. Bei der Formulierung von Produktionspunkten werden häufig folgende Vereinfachungen vorgenommen: (a) Nichtberücksichtigung des zeitlichen Ablaufs innerhalb der Produktionsperiode (die zu verschiedenen Zeitpunkten anfallenden Produktmengen einer gleichen Qualität werden zu einer Produktmenge zusammengefaßt).  Entsprechendes gilt für die Faktorseite, Zwischenprodukte erscheinen nicht explizit usw. (b) Produkte unterschiedlicher Qualität werden zu Produktaggregaten zusammengefaßt, Faktoren unterschiedlicher Qualität zu Faktoraggregaten. (c) Vernachlässigung von konstanten oder nicht knappen Produktionsfaktoren und von unwesentlich erscheinenden Neben- und Abfallprodukten.  Eine Wirtschaftseinheit verfügt normalerweise über viele, meistens sogar über unendlich viele Produktionspunkte. Meistens werden Teilmengen oder die Gesamtmenge der Produktionspunkte durch funktionelle Beziehungen zwischen Mengen der verschiedenen Produktionsfaktoren und damit erzielbaren Mengen verschiedener Produkte dargestellt. In diesem Zusammenhang wird der Begriff Produktionsfunktion verwendet und meistens wie folgt definiert: Eine Produktionsfunktion gibt an, welche Produktionsmengen innerhalb eines festgelegten Zeitraums mit alternativen Faktormengen jeweils hergestellt werden können und welche Beziehungen die Produktmengen und Faktormengen untereinander aufweisen. Die wohl einfachste Produktionsfunktion ist die limitationale linear-homogene Produktionsfunktion, die nur ein Produkt berücksichtigt und eine beliebige Teilbarkeit der Produkt- und Produktionsfaktormengen unterstellt. Ausgehend von einem technisch effizienten Produktionspunkt  O1(i),-V1(i),...,-Vm(i)) besagt sie, daß unendlich viele weitere technisch effiziente Produktionspunkte mit den Produkt- und Faktormengen O1 =lO1(i),V1 =lV1(i),...,lVm(i) für³ 0  existieren. Sie wird manchmal in der Form                                                                                      


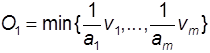
          geschrieben, wobei a1, ..., am (konstante) Produktionskoeffizienten sind. Meistens erfolgt eine Darstellung in der Form                     


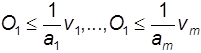
  . Die Formen der Darstellung umfassen auch technisch ineffiziente Produktionspunkte: Eine ProduktionsfaktorkombinationV1,....Vm  ist nämlich nur dann technisch effizient, wenn die Relation                        


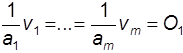
gilt, andernfalls liegt Produktionsfaktorverschwendung vor. Es gilt das Gesetz vom Minimum: Es besteht keine Substitutionsmöglichkeit bei den Produktionsfaktoren, d.h. von einem technisch effizienten Produktionspunkt ausgehend ist es nicht möglich, ein gleichbleibendes Produktionsniveau beizubehalten, wenn die Menge eines Produktionsfaktors vermehrt und dafür die Menge eines anderen Faktors reduziert wird. Weiterhin gibt es keine Vor- und Nachteile der Massenproduktion, d.h. eine Erhöhung aller Produktionsfaktormengen um einen bestimmten Prozentsatz führt weder zu einer überproportionalen noch zu einer unterproportionalen Erhöhung der Produktmenge.  Die limitationale linear-homogene Produktionsfunktion hat sich trotz ihrer Einfachheit bei der Abbildung der Technologien von Wirtschaftseinheiten hervorragend bewährt: Durch geeignete Gliederung der Wirtschaftseinheit in Teilbereiche und durch Formulierung einer Funktion oder mehrerer (alternativ oder in Kombination nutzbarer) Funktionen für jeden Teilbereich sowie durch Berücksichtigung gegebener Faktorbegrenzungen ist es möglich, komplexe Technologien so abzubilden, daß sie in ökonomischen Modellen hinreichend repräsentiert sind. Lineare Programmierung . Produktionsfunktionen, die stetige Substitutionsmöglichkeit zwischen den Produktionsfaktoren zulassen, bilden eine andere Klasse von Produktionsfunktionen (häufig neoklassische Produktionsfunktionen genannt). Diese werden meistens zur Abbildung von Beziehungen zwischen größeren Produkt- und Produktionsfaktoraggregaten verwandt, beispielsweise zur Abbildung der Abhängigkeit der Höhe des realen Sozialprodukts von der Höhe des volkswirtschaftlichen Arbeits- und Kapitaleinsatzes. Wir kennzeichnen eine solche Funktion mit  O = f(V1,...,Vm). Bei ihrer Spezifizierung spielen nachfolgende Definitionen und Beziehungen eine wichtige Rolle: (a) Meistens wird die Gültigkeit des Gesetzes abnehmenden Ertragszuwachses angenommen, d.h. bei laufender Erhöhung der Menge eines Produktionsfaktors und bei Konstanz der übrigen Faktormengen (partielle Faktorvariation) nimmt die Produktmenge nur unterproportional zu                     


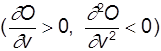
 . Dabei wird die Beziehung zwischen der variablen Faktormenge und der Produktmenge durch eine Produktionselastizität (Elastizitäten) gekennzeichnet. Diese gibt an, um wieviel Prozent sich die Produktmenge ändert, wenn sich die Faktormenge um ein Prozent ändert. (b) Totale Faktorvariation bedeutet eine Veränderung aller Faktormengen um den gleichen Prozentsatz. Je nachdem, ob dies ein Wachstum der Produktmenge um einen größeren, gleichen oder kleineren Prozentsatz auslöst, spricht man von einer Skalenelastizität größer, gleich oder kleiner als eins. Im ersteren Fall liegen Vorteile, im letzteren Nachteile der Massenproduktion vor. Meistens werden Produktionsfunktionen mit einer Skalenelastizität von eins verwandt. (c) Faktorsubstitution bedeutet einen teilweisen oder ganzen gegenseitigen Austausch von Faktormengen zweier oder mehrerer Faktoren derart, daß die Produktmenge konstant bleibt. In diesem Zusammenhang wird mit dem Begriff Grenzrate der Substitution gearbeitet. Die Grenzrate der Substitution gibt an, um wieviel Einheiten die Menge des Faktors abnimmt, wenn die Menge eines anderen Faktors um eine Einheit zunimmt. Sie ist  was mit der Gültigkeit des Gesetzes abnehmenden Ertragszuwachses zusammenhängt  meistens abnehmend, d.h. bei einer Vergrößerung der Relation der Menge des ersten Faktors im Vergleich zur Menge des zweiten Faktors kann durch eine Mengeneinheit des ersten Faktors immer weniger vom zweiten Faktor eingespart werden. Auf der Beziehung zwischen Faktormengenrelation und Grenzrate der Substitution baut die Definition der Substitutionselastizität auf.  Diese gibt an, um wieviel Prozent sich die Relation zwischen den Mengen des ersten und des zweiten Faktors ändert, wenn sich die Grenzrate der Substitution des Faktors in bezug auf den zweiten Faktor um ein Prozent ändert. Je kleiner die Substitutionselastizität ist, desto geringer ist die Substitutionsmöglichkeit.

Literatur: W. Krelle, Produktionstheorie. Tübingen 1969. E. Malinvaud, Lectures on Microeconomic Theory. Amsterdam-London-New York 1972.