Bevölkerungstheorie

Die ökonomische B. hat in den 3 Nachkriegsjahrzehnten, in denen die allgemeine Wirtschaftstheorie unzweifelhaft sehr große Fortschritte gemacht hat, in der wissenschaftlichen Diskussion kaum eine Rolle gespielt. Seit Mitte der 70er Jahre ist allerdings ein zunehmendes Interesse an Fragen der B. zu erkennen. Dies ist zumindest in der Bundesrepublik auf den drastischen Geburtenrückgang seit 1966 zurückzuführen. Das zunehmende Interesse läßt die Vermutung zu, daß sich der Kenntnisstand in Zukunft rasch verändern wird. Drei Teilgebiete haben zur Weiterentwicklung der B. beigetragen:
1.                        die  formale Demographie, insbesondere die bevölkerungsdynamischen          Modelle,
2.                        die neoklassische Wachstumstheorie (Wachstumstheorie), zumindest  insoweit die Wachstumsrate der Bevölkerung endogen bestimmt ist, und schließlich
3.                        die zum Teil aus der Soziologie stammenden Überlegungen zur langfristigen Entwicklung der Geburtenraten beziehungsweise ihrer Abhängigkeit von derwirtschaftlichen Entwicklung. ad
1. : Der zentrale Begriff der Bevölkerungsdynamik ist der der "stabilen Bevölkerung". Er ist durch folgende Annahmen definiert: a)          Die altersspezifische Mortalität ist konstant. Die Wahrscheinlichkeit p (x) für einen Neugeborenen, das Alter x zu erreichen, ist also von der Zeit t unabhängig. b)          Die betrachtete Bevölkerung ist abgeschlossen, ihre Zahl kann also durch Migration nicht verändert werden. c)          Die Geburtenzahl B (t) verändert sich mit einer konstanten Rate n:                             B (t) = B
(0) · ent,                             wobei B (t) : = Zahl der Geburten im Zeitpunkt t,               n : = Wachstumsrate der Geburten. Wie groß ist die Zahl der Individuen, die im Zeitpunkt t zwischen x und x + dx Jahre alt sind? Dazu muß man in der Zeit um x Jahre zurückgehen. Die Zahl der Geburten im Zeitpunkt t-x betrug nämlich:            


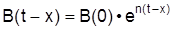
Da wir nicht ein präzises Alter, sondern das Altersintervall x + dx betrachten, beträgt die Anzahl der Geburten: B
(0) · en(t-x) Nicht alle in dem Intervall Geborenen haben überlebt. Die Anzahl der im Zeitpunkt t zwischen x und x + dx Jahre alten Personen ist daher:
(1)    


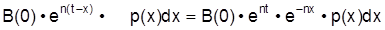
Die Gesamtzahl der Bevölkerung ergibt sich durch Integration über alle Altersgruppen:
(2)    


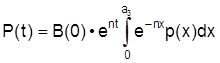
,                      wobei    P (t) := Gesamtbevölkerung;               a3    := Höchstalter. Wegen der Konstanz des Integrals folgt, daß die Wachstumsrate der Bevölkerung (P) leich der Wachstumsrate der Geburten ist: P = n. Der Anteil einer beliebigen x + dx-jährigen Bevölkerung an der Gesamtbevölkerung kann mit Division von
(1) durch
(2) ermittelt werden und ist konstant:            


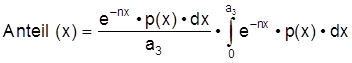
                                                      Man kann auch zeigen, daß eine Bevölkerung, die die Voraussetzungen a) bis c) erfüllt, rasch zu einer Bevölkerung mit konstanter Altersstruktur konvergiert. Im Bereich der formalen Demographie sind viele weitere Zusammenhänge mathematisch bewiesen und stellen die erste Quelle bevölkerungstheoretischer Überlegungen dar (Keyfitz, 1977). ad
2. : Ein weiterer Modellrahmen, in dem bevölkerungstheoretische Überlegungen angestellt werden, ist die neoklassische Wachstumstheorie. Aufgrund der Modellannahmen dieser Theorie lassen sich viele Zusammenhänge bei "gleichgewichtigem Wachstum" ableiten. Bevölkerungstheoretische Zusammenhänge bei exogener Wachstumsrate (vgl. exogene Variable) der Bevölkerung gA ergeben sich insbesondere aus folgenden Beziehungen (vgl. Krelle, 1985):             gY = gA + ga  , wobei    gY              : =        Gleichgewichtswachstumsrate des Sozialprodukts            gA         : =        exogene Wachstumsrate der Arbeitszeit bzw. der Bevölkerung ch     ga        : =        Wachstumsrate der Arbeitsproduktivität . Unter den i.d.R. zugrundegelegten Annahmen hängt das gleichgewichtige Pro-Kopf-Einkommen (y) negativ mit der Wachstumsrate der Bevölkerung (gA) und positiv mit der Kapitalintensität (gK) zusammen:          y = f (gK). Eine positive Beziehung zwischen Bevölkerungswachstumsrate und Pro-Kopf-Einkommen ergibt sich aber, wenn man unterstellt, daß der technische Fortschrit positiv von der Bevölkerungswachstumsrate abhängt (dazu: Simon, 1977; Steinmann, 1986). Einige wenige Versuche von endogenen Erklärungen der Wachstumsrate der Bevölkerung haben wenig Beifall gefunden. Die in diesen Modellen verwendeten malthusianischen Populationsfunktionen erklären die gegenseitige Abhängigkeit von ökonomischen und demographischen Größen auf allzu einfache Weise (dazu: Schmitt-Rink, 1985). ad
3. : Die Beziehung zwischen der Geburtenrate und dem wirtschaftlichen Rahmen ist in Wirklichkeit sehr kompliziert. Eine erste grobe Vorstellung von dieser Beziehung hat Leibenstein 1957 gegeben. Sein Anliegen war, die im Längsschnitt überall beobachtbare negative Korrelation (Korrelationsanalyse) zwischen steigendem realem Pro-Kopf-Einkommen und sinkenden Geburtenraten zu erklären. Der Ansatz von Leibenstein wurde von Becker weiterentwickelt (Becker, 1960). Es scheint, daß die Entscheidung der Mutter oder der Familie, eine bestimmte Zahl von Kindern zu haben, historisch gesehen eine rationale Entscheidung war und auch heute eine solche ist. Bei der Entscheidung werden Nutzen und Kosten verglichen. Nach Leibenstein gibt es zwei Gruppen von Nutzen: Konsumnutzen, das heißt die bloße Freude an Kindern, und Investitionsnutzen, der vor allem darin liegt, daß Kinder bei Alter und Krankheit der Eltern materielle und emotionale Sicherheit bieten. Über die langfristige Entwicklung des Konsumnutzens lassen sich naturgemäß keine Aussagen machen. Der früher entscheidende Investitionsnutzen jedoch hat seine Bedeutung heute sicher sehr weitgehend verloren. Auf der Kostenseite kann man direkte Kosten (Erziehung, Ernährung) und indirekte Kosten (Opportunitätskosten, die durch den  Einkommensverlust der sonst berufstätigen Ehefrau entstehen) unterscheiden. Die indirekten Kosten haben, wie man statistisch gut belegen kann, drastisch zugenommen. Diese Entscheidung der Eltern müßte in einem bevölkerungstheoretischen Gesamtmodell eine zentrale Stellung haben. Ein solches Modell sollte einerseits erklären, warum sich die ökonomischen Variablen im Zeitablauf so ändern, daß sich die Eltern für weniger Kinder entscheiden. Andererseits müßte der Einfluß der Veränderung der Geburtenrate auf die langfristige Wirtschaftsentwicklung aufgezeigt werden können. Obwohl bevölkerungsdynamische Modelle (ad
1.) und neoklassische Wachstumstheorie (ad
2.) sehr ähnliche theoretische Konzepte darstellen, weil die wichtigsten Ergebnisse beider Theorien als asymptotische, also sehr langfristige, Aussagen zu verstehen sind, hat dies bisher nicht zu einer Integration der beiden Theorien geführt. Die Konkretisierung bevölkerungsökonomischer Theorievorstellungen (vgl. Felderer, 1983; Felderer/Sauga, 1988) hat noch nicht den Stand befriedigender formaler Modelle erreicht.

Literatur: G. S. Becker, An Economic Analysis of Fertility, in: Demographic and Economic Change in Developed Countries, National Bureau of Economic Research (Hrsg.). Princeton 1960. B. Felderer, Wirtschaftliche Entwicklung bei schrumpfender Bevölkerung. Berlin-Heidelberg-New York-Tokio 1983. B. Felderer/M. Sauga, Bevölkerung und Wirtschaftsentwicklung. Frankfurt 1988. N. Keyfitz, Applied Formal Demography. New York 1977. W. Krelle, Theorie des wirtschaftlichen Wachstums. Berlin-Heidelberg-New York-Tokio 1985. G. Schmitt-Rink, Demographische Variablen in der ökonomischen Wachstumstheorie, in: Felderer, B. (Hrsg.), Beiträge zur Bevölkerungsökonomie. Berlin 1986. J. Simon, The Economics of Population Growth. Princeton 1977. G. Steinmann, Bevölkerungsentwicklung und technischer Fortschritt, in: B. Felderer (Hrsg.), Beiträge zur Bevölkerungsökonomie, Berlin 1986.