bilateraler Tausch

1. Für einen freiwilligen Tausch zwischen zwei Wirtschaftssubjekten ist die Zustimmung beider notwendig. Bei rationalem Verhalten folgt daraus, daß keiner dadurch schlechtergestellt wird als vor dem Tausch, und im Regelfalle beide bessergestellt werden, weil sonst kein Anreiz zum Tausch besteht. Vom Gelde als Tauschgut soll hier abstrahiert werden, ebenso von einem Tausch mit mehr als zwei Beteiligten, also z.B. einem Ringtausch, bei dem der Partner, von dem man etwas bekommt, ein anderer ist als derjenige, dem man etwas gibt. Ein isolierter Tausch liegt vor, wenn die Tauschpartner keine alternativen Tauschmöglichkeiten haben, also Wettbewerber nicht vorhanden sind. Es besteht somit die Situation des bilateralen Monopols (Monopol), wenn im folgenden nichts anderes angegeben ist. Die Gründe für den Tausch können einmal in den unterschiedlichen Produktionsmöglichkeiten liegen. Dies wird in der Theorie der komparativen Kosten behandelt. Zum anderen kann die unterschiedliche Nutzenschätzung (Nutzen, Präferenzen) der Wirtschaftssubjekte den Tausch begründen. Dies soll hier behandelt werden, wobei eine dritte Begründung für Tausch, nämlich die unterschiedliche Grenzproduktivität von Produktionsfaktoren , in voller Analogie dazu steht.
2. Der b. zwischen den Wirtschaftssubjekten A und B wird mit Hilfe einer Edgeworth-Box (Figur 1) dargestellt. Sie besteht aus den zwei Koordinatensystemen von A und B für die beiden Güterarten X und Y. Der Nullpunkt des Koordinatensystems von B liegt in demjenigen von A an der Stelle, die durch die Summe der den beiden Wirtschaftssubjekten zur Verfügung stehenden jeweiligen Gütermengen gegeben ist.                        


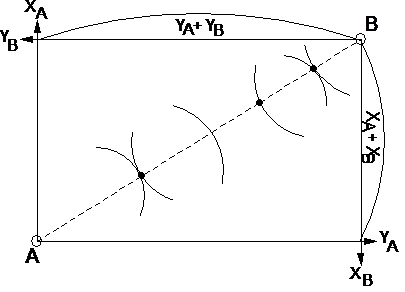
Durch die Konstruktion des Diagramms gibt jeder Punkt in ihm eine bestimmte Aufteilung der Gesamtgütermengen auf die beiden Wirtschaftssubjekte an. Für jedes der Wirtschaftssubjekte ist ein Indifferenzkurvensystem (Indifferenzkurve, Indifferenzkurvenanalyse) eingezeichnet, mit dessen Hilfe die Bewertung der Güterkombinationen erfolgt. Wenn nun die Ausgangsausstattung durch den Punkt 1 gegeben ist, dann bilden die durch diesen Punkt gehenden Indifferenzkurven der Wirtschaftssubjekte eine Linse. Alle zwischen den Punkten 1 und 2 liegenden Güterverteilungen werden von beiden Wirtschaftssubjekten besser beurteilt als die Ausgangsverteilung. Sie sind erreichbar durch Tausch, wobei z.B. der A von B DX bekommt und dafür DY an B abgibt. Durch diesen Tausch gelangt man zum Punkt
3. Beide Wirtschaftssubjekte befinden sich jetzt auf einer einen höheren Nutzen anzeigenden Indifferenzkurve. Da jedoch für diesen Punkt wiederum eine schraffiert gezeichnete Linse existiert, sind die Tauschmöglichkeiten noch nicht erschöpft. Die beiden Tauschpartner könnten sich also durch einen weiteren Tausch verbessern. Solche Verbesserungsmöglichkeiten sind nicht mehr gegeben, wenn ein Punkt erreicht wird, in dem sich die Indifferenzkurven der beiden Tauschpartner gerade berühren, wie in den Punkten 4 bis
7. Die endgültigen Tauschkontrakte werden also in solchen Punkten liegen, die man deshalb auch zu der sogenannten Kontraktkurve zusammenfaßt. Für den Ausgangspunkt 1 sind alle Punkte auf der Kontraktkurve zwischen den Punkten 4 und 5 als endgültige Verteilungen erreichbar. Das Tauschverhältnis DX zu DY ist damit nicht eindeutig, sondern nur in einer gewissen Bandbreite bestimmt, wie es der Situation des bilateralen Monopols entspricht. Der Vorteil, den beide Partner aus dem Tausch gewinnen können, kann daher auch auf sie ganz verschieden verteilt sein.
3. Zu einer größeren Bestimmtheit des Ergebnisses gelangt man, wenn dem einzelnen Tauschpartner das Tauschverhältnis vorgegeben ist. Dies kann in einer Wettbewerbssituation der Fall sein, in der der Preis vorgegeben ist und das Wirtschaftssubjekt nur noch seine Menge optimal anpaßt. In der Edgeworth-Box wird ein Tauschverhältnis durch eine Gerade durch den Ausgangspunkt 1 dargestellt (Figur 2).                        


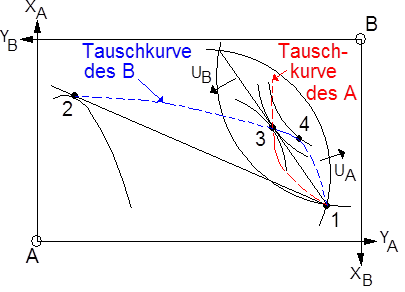
Der für den B günstigste Umfang des Tausches ergibt sich nun an der Stelle, an der die Tauschgerade von der am weitesten außen liegenden Indifferenzkurve des B tangiert wird. Dies ist am Punkt 2 demonstriert. Für andere Tauschverhältnisse lassen sich entsprechende Punkte bestimmen, die alle zu einer Tauschkurve des B zusammengefaßt werden können. Auch für den A läßt sich eine solche Tauschkurve einzeichnen. Die Tauschkurve des A und des B schneiden sich in Punkt 3, d.h. bei dem diesem Punkt entsprechenden Tauschverhältnis ist der gewünschte Umfang des Tausches bei beiden Wirtschaftssubjekten miteinander vereinbar. Dieser Punkt entspricht also dem Wettbewerbsgleichgewicht (Gleichgewicht), bei dem zum Gleichgewichtspreis die angebotene und die nachgefragte Menge übereinstimmen. Wenn nur einer der beiden Partner, z.B. B sich als Mengenanpasser verhält, kann der andere den für ihn günstigsten Punkt auf der Tauschkurve des ersten wählen. Dies ist z.B. Punkt 4, weil dort die Tauschkurve des B von der höchstmöglichen Indifferenzkurve des A tangiert wird. Das entspricht einem Monopol des A, wobei im Hinblick auf die nun zu besprechenden Optimalitätseigenschaften darauf hinzuweisen ist, daß dieser Punkt nicht auf der Kontraktkurve liegt.
4. Tauschlösungen, die auf der Kontraktkurve liegen, stellen ein Paretooptimum dar, d.h. daß sich keines der Wirtschaftssubjekte verbessern kann, ohne daß das andere schlechtergestellt wird. Nur in den Punkten auf der Kontraktkurve gibt es keine Linse, die eine Verbesserung durch Tausch ermöglicht, ohne daß der andere schlechtergestellt wird. Man kann die Paretooptimalität zur Norm für die gesamte Volkswirtschaft erklären, wobei dann die Verwirklichung dieses Prinzips im Konsumsektor dem sogenannten Verbrauchsoptimum entspricht. Dieses läßt sich sehr einfach mit Hilfe der Edgeworth-Box demonstrieren. Die Allokation der Konsumgütger (Güter) X und Y, deren vorhandene Gesamtmengen dem Punkte B entsprechen, ist nur in den auf der Kontraktkurve liegenden Punkten optimal. Die Verteilung des Wohlstandes auf die Wirtschaftssubjekte A und B entlang der Kontraktkurve ist jedoch sehr verschieden. Durch die Definition des Paretooptimums ist daher die Verteilung des Wohlstandes nicht festgelegt. Zur Definition des gesamtwirtschaftlichen Optimums ist deshalb eine zusätzliche Verteilungsnorm erforderlich.

Literatur: V. Pareto, Manuale d’economie politica. Milano 1906 (engl. Übersetzung: Manual of Political Economy. New York 1971). E. Schneider, Einführung in die Wirtschaftstheorie, II. Teil.
8. A., Tübingen 1963. E. Sohmen, Allokationstheorie und Wirtschaftspolitik. Tübingen 1976.