|
Diffusion
Inhaltsübersicht
I. Grundlagen und Begriffe
II. Diffusionstheorie
III. Das klassische Diffusionsmodell von Rogers
IV. Differenzialgleichungsmodelle
V. Neuere Diffusionsmodelle
I. Grundlagen und Begriffe
Die Diffusionsforschung in den Sozialwissenschaften befasst sich mit der Ausbreitung von Neuerungen, speziell von Informationen, Verfahren und Produkten. Diffusion wurde bei Ausbreitungsanalysen für Produkte und Verfahren zunächst als das Ergebnis eines sozialen Prozesses interpretiert, in dessen Verlauf Informierte oder Nutzer neuer Produkte oder Verfahren weitere potenzielle Übernehmer informieren und beeinflussen.
Zunehmend traten aber Zweifel auf, ob Kommunikation und Imitation auf Nachfrager- bzw. Anwenderseite Ausbreitungsverläufe von Produkten und Verfahren ausreichend erklären können. Seit Mitte der 1970er-Jahre hat sich die Meinung durchgesetzt, dass Diffusion nicht mehr allein als das Resultat von sozialen Interaktionen zwischen Nachfragern, sondern als deren Reaktion auf Marketing-Maßnahmen und auf andere Faktoren zu begreifen ist. Diffusion ist damit ein Gegenstand des Innovationsmanagements geworden.
Diffusionsverläufe von Innovationen entstehen, weil Interessenten eine Innovation (im Marketing meist: neues Produkt, neuartige Dienstleistung) nicht zeitgleich mit deren Markteinführung, sondern nach und nach, also zeitlich verteilt übernehmen. Die Anbieter setzen einen Diffusionsprozess in Gang, der sich als zeitliche Verteilung des Übernahmezeitpunkts (Diffusion) beobachten lässt (vgl. Abb. 1). Übernahmeeinheiten sind z.B. Unternehmen, Haushalte oder Einzelpersonen. Die maximale Anzahl der Übernahmeeinheiten, die als Übernehmer einer Innovation in Betracht kommen, bildet das Übernehmerpotenzial, bezüglich dessen sich die Innovation allmählich ausbreitet. Im Zeitablauf verändert das Potenzial daher seine anteilige Zusammensetzung, bestehend aus den Teilen
| - | offenes Potenzial: Übernahmeeinheiten, die noch nicht über die Innovation und ihre Eigenschaften unterrichtet sind, | | - | Übernahmekandidaten: Übernahmeeinheiten, die erst einen Übernahmeentscheidungsprozess durchlaufen oder mit der Übernahme noch zögern, und | | - | Übernehmerbestand: Übernahmeeinheiten, die die Innovation bereits übernommen haben. |
Der Diffusionsverlauf von Produkten wird meist als ein Teil des Produktlebenszyklus begriffen. Während dieser die zeitliche Verteilung der Absatzzahlen angibt, bezeichnet der Diffusionsverlauf meist nur die zeitliche Verteilung des Zeitpunkts des erstmaligen Kaufs des neuen Produkts. Wiederkauf- und Kaufvolumenaspekte werden also nicht betrachtet. Lediglich bei häufig erworbenen Verbrauchsgütern wird bisweilen nicht der Zeitpunkt des ersten Kaufs, sondern jener der Akzeptanz analysiert.
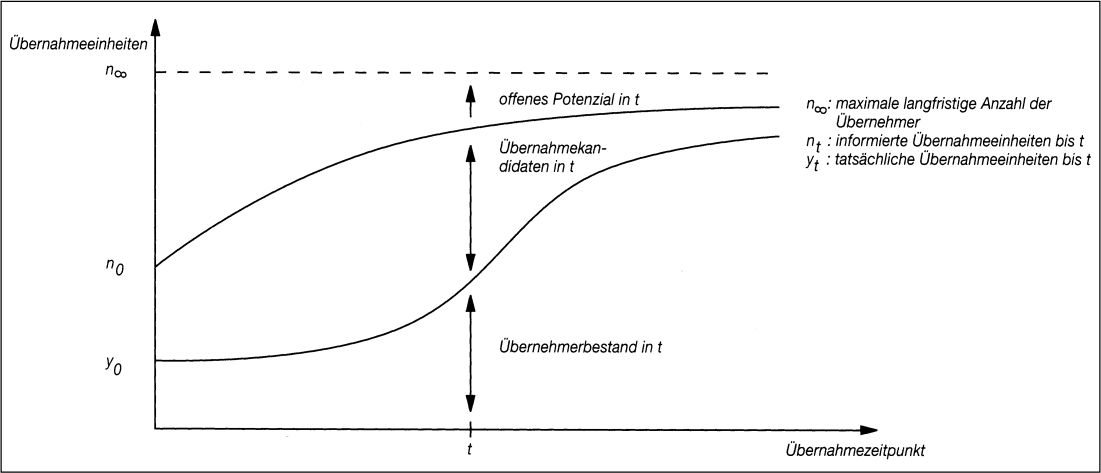
Abb. 1: Idealtypischer Verlauf einer Diffusion
Diffusionsverläufe von Produkten werden untersucht, um den zukünftigen Verlauf der Übernahmen kurzfristig planen zu können, Verständnis über die Wirkung von Einflussgrößen (z.B. Preise, Werbemaßnahmen) auf einen Diffusionsverlauf zu erlangen und Marktgesetzmäßigkeiten bei der Marktbearbeitung von ähnlichen, neuen Produkten berücksichtigen zu können.
II. Diffusionstheorie
Für unterschiedliche Übernahmezeitpunkte durch potenzielle Übernehmer sind im Wesentlichen drei Ursachen verantwortlich.
Durch die Markteinführung einer Innovation sind nicht unverzüglich alle möglichen Übernehmer über die Existenz der Innovation und deren Nutzungsmöglichkeiten informiert. Marktkommunikation durch Anbieter oder Kommunikation auf Seiten der Nachfrager ist erforderlich, damit potenzielle Übernehmer hiervon unterrichtet und somit zu Übernahmekandidaten werden. Da nicht jeder potenzielle Übernehmer zum gleichen Zeitpunkt diese Information erhält, ist der Beginn der Übernahmeentscheidungsprozesse unterschiedlich.
Auch Übernahmekandidaten reagieren nicht notwendigerweise sofort mit der Übernahme. Sie sammeln Informationen, bewerten diese und legen gegebenenfalls einen Übernahmezeitpunkt fest. Somit ist auch die Dauer der Entscheidungsprozesse unterschiedlich.
Mögliche Resultate eines Übernahmeentscheidungsprozesses sind die Ablehnung der Innovation, ihre sofortige Übernahme oder die Festlegung eines künftigen Zeitpunkts für den Übernahmevollzug bei späterem Bedarf. Die Zeitspanne zwischen positiver Entscheidung und Vollzug kann variieren. Erst mit dem Übernahmevollzug werden die Übernahmekandidaten zu Übernehmern.
Der Diffusionsprozess spiegelt die Häufigkeit des Übernahmevollzugs in den einzelnen Perioden wider. Die Ursachen für die Form der Häufigkeitsverteilung sind in den Einflussgrößen auf den Beginn der Übernahmeentscheidungsprozesse, deren Dauer und deren Resultate zu suchen.
III. Das klassische Diffusionsmodell von Rogers
In kaum einem einführenden Lehrbuch zum Marketing fehlt das Diffusionsmodell von Rogers (vgl. Abb. 2), das die Verteilung des Übernahmezeitpunkts einer Innovation als Glockenkurve (Normalverteilung) wiedergibt (Rogers, E. M. 1983, S. 247).
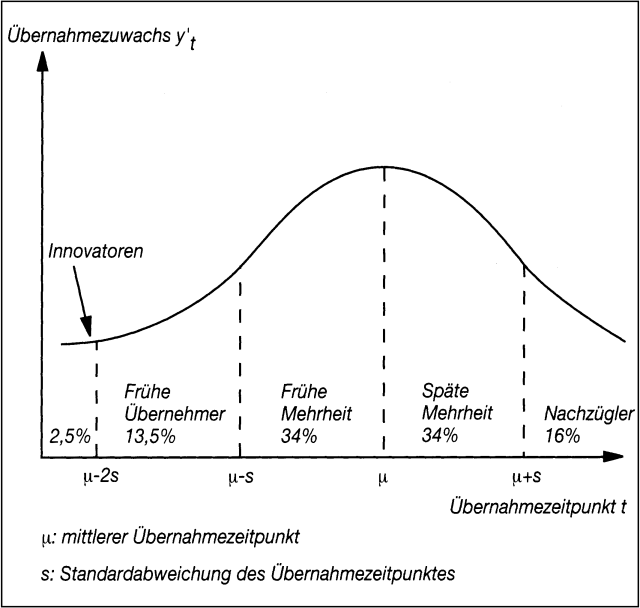
Abb. 2: Das Diffusionsmodell von Rogers
Nach Maßgabe des Übernahmezeitpunkts werden die Übernehmer als Innovatoren, frühe Übernehmer, frühe Mehrheit, späte Mehrheit und Nachzügler bezeichnet.
Rogers sieht die Unterschiede bei der Diffusion verschiedener Innovationen (Produkte, Verfahren) in deren Eigenschaften selbst begründet. Eine Innovation breitet sich – wie in empirischen Studien auch meist bestätigt werden konnte – im Vergleich zu anderen Innovationen umso rascher aus,
| - | je mehr sie Konkurrenzprodukten bzw. -verfahren überlegen ist, | | - | je mehr sie mit Werten, Erfahrungen und bestehenden Strukturen bei den potenziellen Übernehmern kompatibel ist, | | - | je einfacher sie verstanden werden kann, | | - | je risikoloser die Übernahmeentscheidung ist (z.B. probeweise Übernahme) und | | - | je leichter sich Ergebnis und Wirkung einer Übernahme darstellen lassen. |
Der glockenförmige Verlauf der Übernahmezeitpunkte einer einzelnen Innovation wird hier auf einen Imitationsprozess zurückgeführt. Eine Diffusion nimmt einen solchen Verlauf, wenn die Annahmen des logistischen Modells gültig sind. Dieses Modell besagt: »Je höher der Anteil der bisherigen Übernehmer der Eigenschaft (hier: Wissen, Neuerung, Produkt) ist, umso höher ist die Wahrscheinlichkeit, dass auch eine Einheit, die die Eigenschaft noch nicht übernommen hat (hier: Übernahmekandidat), sie übernimmt.« Dies lässt sich formal wie folgt ausdrücken:
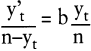

Wird diese Differenzialgleichung nach yt aufgelöst, so resultiert die logistische Funktion (Lösung siehe Tab. 1). Deren Ableitung y\'t liefert eine der Normalverteilung sehr stark ähnelnde Glockenkurve.

Tab. 1: Einige Lösungen der Differenzialgleichungen
Hinter dem logistischen Modell bzw. der Normalverteilung verbirgt sich folglich die Annahme, dass das Urteil der Nachfrager über die Attraktivität der Übernahme eines Produkts stark vom Anteil der bisherigen Übernehmer abhängt. Einige wichtige Fälle, in denen dies gelten kann, sind Folgende:
| - | Das wichtigste Übernahmemotiv besteht in sozialer Anerkennung. In bestimmten Segmenten steigt der soziale Druck zur Imitation mit dem Übernehmerbestand, etwa bei modischen Produkten oder Produkten als Kennung für eine Cliquenzugehörigkeit (Mansfield, E. 1961; Bass, F. M. 1969). | | - | Der Übernehmerbestand bestimmt die Einsatzmöglichkeiten des Produktes (z.B. bei Kommunikationseinrichtungen). | | - | Das wichtigste Übernahmemotiv bildet der Fundus an Produkterfahrung, der von Beratern oder von Personen mit Meinungsführereigenschaft weitergegeben wird und stellvertretendes Lernen ermöglicht. Erfahrungsberichte helfen, in dem Maße Fehler zu vermeiden, wie solche bereits von Übernehmern begangen worden sind (Mansfield, E. 1961). |
Da diese Annahme nur für spezielle Fälle und bei häufigen Interaktionen auf Übernehmerseite gilt, folgen reale Diffusionsverläufe selten einer idealtypischen Normalverteilung, sondern nehmen eigene, charakteristische Formen an.
IV. Differenzialgleichungsmodelle
In den sechziger und frühen siebziger Jahren wurden Modifikationen der logistischen Funktion entwickelt, um Ausbreitungsprozesse neuer Produkte besser erklären und für die nähere Zukunft genauer prognostizieren zu können. In diesen Modellen wird weiterhin unterstellt, dass durch Eingriffe von außen kein Einfluss auf den Diffusionsverlauf genommen wird. Diese Modelle haben für praktische Anwendungen heute noch eine große Bedeutung, so etwa das »Bass-Modell« (Bass, F. M. 1969). Ein Differenzialgleichungsmodell, in dem viele häufig empirisch eingesetzte Spezialmodelle enthalten sind, und eine spezielle Interpretation sind nachfolgend kurz skizziert (Dodson, J. A./Muller, E. 1978; Mahajan, V./Peterson, R. A. 1978):
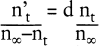
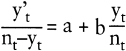

Die Wahrscheinlichkeit, dass eine der n∞ – nt noch nicht informierten Übernahmeeinheiten informiert wird (n\'t: Zuwachs an Informierten in t), hängt linear vom Anteil der bereits Informierten nt/n∞ ab. Auch zwischen der Wahrscheinlichkeit, dass einer der nt – yt Übernahmekandidaten übernimmt (y\'t: Zuwachs an Übernehmern in t), und dem Anteil der Übernehmer yt/nt bis zu diesem Zeitpunkt besteht eine lineare Beziehung.
Die Parameter b bzw. d bringen den Effekt sozialer Interaktion auf Nachfragerseite zum Ausdruck, a und c jeweils »konstante diffusionsexogene« Effekte (z.B. konstante Werbeintensität des Anbieters).
Die Lösungen der beiden Differenzialgleichungen ergeben je Parameterkonstellation charakteristische Diffusionsfunktionen.
Die Kenntnis der Diffusionsfunktionen ist für die Schätzung der Modellparameter hilfreich. Falls die Parameter von nicht lösbaren Differenzialgleichungen geschätzt werden sollen, wird meist auf diskrete Modellformulierungen ausgewichen. Letzteres gilt etwa für die im Folgenden genannten Modelle.
In den späteren siebziger Jahren war die Diffusionsforschung darauf konzentriert, komplexere Differenzialgleichungsmodelle zu diskutieren und an realen Diffusionsverläufen zu überprüfen. Anstelle des linearen Gleichungstyps wurden andere Funktionen gewählt. Die Zeit t kam als statistisch erklärende Variable hinzu.
Daneben wurden verschiedene Diffusionsmodelle für einzelne Segmente von Übernahmeeinheiten entwickelt. So unterschied Kaas die beiden Segmente Meinungsführer und Meinungsfolger, um den unterschiedlichen Einfluss dieser Personen auf die Verbreitung von Information und auf den Imitationsdruck hinsichtlich der Übernahme der Produkte zu modellieren (Kaas, K. P. 1973). Schmalen schlug vor, die Diffusion getrennt in einem Innovatoren- und einem Imitatoren-Segment wie folgt abzubilden (Schmalen, H. 1979):
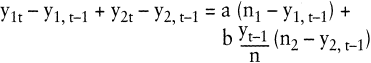
Die Übernahmewahrscheinlichkeit der Übernahmeeinheiten im Innovatoren-Segment (Übernehmerpotenzial n1, Übernehmerzuwachs y1t – y1,t – 1, Übernehmerbestand y1t) ist gemäß diesem Modell im Zeitablauf konstant (hier: a), im Imitatoren-Segment (Potenzial n2, Zuwachs y2t – y2,t – 1, Bestand y2t) hängt sie proportional vom Übernehmeranteil (yt/n, wobei n=n1+n2, yt=y1t+y2t) ab.
Modelle dieser Kategorie eignen sich zur Abbildung und für die kurzfristige Prognose von Ausbreitungsverläufen, wenn die Bekanntheit und das Urteil über die Attraktivität einer Übernahme zumindest weitgehend durch soziale Interaktion zwischen den Übernahmeeinheiten bestimmt werden und in die Verläufe von außen, z.B. durch Marketing-Politik, nicht eingegriffen wird. Für langfristige Prognosen auf der Grundlage einer kaum vorangeschrittenen Diffusion haben sich diese Modelle nicht bewährt.
V. Neuere Diffusionsmodelle
Der Übernehmeranteil kann als diffusionsendogene Variable z.B. zur Modellierung von sozialem Einfluss und des Erfahrungsfundus verwendet werden. Ab Mitte der siebziger Jahre wurden auch Diffusionsmodelle mit diffusionsexogenen Variablen hinsichtlich ihrer Eignung, Marketing-Aktivitäten zu planen und Übernehmerzahlen zu prognostizieren, erprobt. Zu den diffusionsexogenen Variablen sind beispielsweise die Preis-, Werbe- oder Außendienstpolitik des Anbieters der Innovation und seiner Wettbewerber sowie ökonomische und rechtliche Veränderungen zu zählen. Entweder werden diese exogenen Größen direkt in die Modelle aufgenommen, oder es wird die Wirkung dieser Variablen implizit in Form von Koeffizienten ausgedrückt.
Letzteres gilt für einen weiteren Vorschlag von Schmalen. In diesem Modell mit heterogen auf exogene Variablen reagierendem Potenzial wird die Struktur des semilogistischen Modells noch weitgehend beibehalten, aber berücksichtigt, dass sich exogene Variablen in verschiedenen, noch geeignet abzugrenzenden Übernehmersegmenten unterschiedlich auf die Übernahmewahrscheinlichkeit auswirken können (Schmalen, H./Binninger, F.-M./Pechtl, H. 1993):
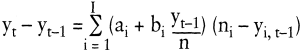

In vielen empirisch eingesetzten Modellformulierungen wird einfachheitshalber angenommen, dass Übernahmeeinheiten auf exogene Variablen homogen reagieren. Auf eine Unterteilung der Nachfrager in Segmente wird in diesen Untersuchungen verzichtet (Hesse, H.-W. 1987; Simon, H./Sebastian, K.-H. 1987). Die funktionale Beziehung (z.B. additiv, multiplikativ, Interaktionsterme) und die berücksichtigten exogenen Variablen (z.B. Schulungsmaßnahmen, Messebelegung, Eingriffe des Gesetzgebers) werden fallspezifisch festgelegt.
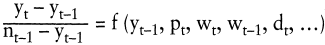

Dabei wird beachtet, dass manche exogene Variablen zeitliche Ausstrahlungseffekte aufweisen. Beispielsweise wirken Werbemaßnahmen nicht nur in der Periode ihrer Durchführung, sondern auch noch in späteren Zeiträumen. Gegebenenfalls sollten also zeitverzögerte exogene Variablen berücksichtigt werden.
In der Diffusionstheorie werden die Fragen behandelt, auf welche Weise Anbieter die Geschwindigkeit der Ausbreitung neuer Produkte beeinflussen können und welche Nachfragersegmente bevorzugt in welchen Marktphasen eines Produkts übernehmen. Da es für viele Unternehmen von existenzieller Bedeutung ist, dass ihre neuen Produkte in kurzer Zeit Marktbedeutung erlangen, und da angenommen wird, dass die Ausbreitung durch exogene Variablen beschleunigt werden kann, kann der Einsatz von Diffusionsmodellen ein hilfreiches Planungsinstrument für die Festlegung der absatzpolitischen Aktivitäten und für die Prognose der Übernehmeranzahlen sein. Da zu frühen Zeitpunkten eines Ausbreitungsverlaufs die Datenbasis oft noch klein ist, sollte aufgrund der hohen Fehlerrate von Befunden auch auf Ergebnisse bei ähnlichen Produkten zurückgegriffen und durch subjektive Schätzungen und eventuell Computersimulationen ergänzt werden.
Literatur:
Bass, F. M. : A New Product Growth Model for Consumer Durables, in: Man.Sc., 1969, S. 215 – 227
Dodson, J. A./Muller, E. : Models of New Product Diffusion through Advertising and Word-of-Mouth, in: Man.Sc., 1978, S. 1568 – 1578
Hesse, H.-W. : Kommunikation und Diffusion von Produktinnovationen, Berlin 1987
Kaas, K. P. : Diffusion und Marketing, Stuttgart 1973
Mahajan, V./Peterson, R. A. : Innovation Diffusion in a Dynamic Potential Adopter Population, in: Man.Sc., 1978, S. 1589 – 1597
Mansfield, E. : Technical Change and the Rate of Imitation, in: Econometrica, 1961, S. 741 – 766
Rogers, E. M. : Diffusion of Innovations, 3. A., New York et al. 1983
Schmalen, H. : Marketing-Mix für neuartige Gebrauchsgüter, Wiesbaden 1979
Schmalen, H./Binninger, F.-M./Pechtl, H. : Diffusionsmodelle als Entscheidungshilfe zur Planung absatzpolitischer Maßnahmen bei Neuprodukteinführung, in: DBW, 1993, S. 513 – 527
Simon, H./Sebastian, K.-H. : Diffusion and Advertising, in: Man.Sc., 1987, S. 451 – 466
|