|
Personaleinsatzplanung
Inhaltsübersicht
I. Terminologische und konzeptionelle Grundlagen
II. Ziele der Personaleinsatzplanung
III. Modellansätze zur Personaleinsatzplanung
IV. Kritische Würdigung
I. Terminologische und konzeptionelle Grundlagen
1. Terminologische Grundlagen
Unter Personaleinsatzplanung verstehen wir in Anlehnung an Schweitzer (Schweitzer, 1987, S. 11) und Kossbiel (Kossbiel, 1988, S. 1053) die bewusste, frühzeitige, informationsverarbeitende und geordnete Vorbereitung künftiger Zuordnungen von Arbeitskräften zu Allokationsobjekten. Aus dieser Begriffsbeschreibung geht zum einen hervor, dass wir nur dann von Personaleinsatzplanung sprechen, wenn sich der Planer dessen bewusst ist, dass er Einsatzentscheidungen vorbereitet. Rein zufällige, nicht auf Willensakten des Planers basierende Personalzuordnungen werden somit ausgegrenzt. Die Definition stellt zum anderen auf die Charakteristika der Frühzeitigkeit und der prozeduralen Ordnung der korrespondierenden Zuordnungen ab, d.h. improvisatorisch (spontan) getroffene Allokationsentscheidungen, bei denen auf eine sorgfältige Analyse des Entscheidungsfeldes (Stichwort: Informationsverarbeitung) verzichtet wird, fallen nicht unter den Begriff der Personaleinsatzplanung. Darüber hinaus stellt die obige Definition darauf ab, dass es sich bei der Personaleinsatzplanung um, einen Prozess handelt, bei dem Zuordnungsentscheidungen vorbereitet und nicht notwendigerweise umgesetzt werden, Planrevisionen zu späteren Zeitpunkten mithin zulässig sind. Des weiteren führen wir aus, dass Arbeitskräfte Allokationsobjekten zugeordnet werden: Mit Arbeitskräften sind entweder konkret identifizierbare Individuen (sog. Individual- oder Namensebene) oder (z.B. nach Qualifikationen differenzierte) Kategorien von Arbeitskräften (sog. Kategorialebene) gemeint. Allokationsobjekte können sich nach Maßgabe der zu planenden Einsatzdimensionen (s. I.2.) neben Einsatzzeiträumen und Einsatzorten auf einzelne Tätigkeiten oder auf Tätigkeitskategorien und somit auf sämtliche betrieblichen Leistungs-, Schulungs- und Ausleihprozesse beziehen (Kossbiel, 1992, Sp. 1654 f.).
2. Konzeptionelle Grundlagen
Mit der Personaleinsatzplanung sind neben einer Konnexions- (Verbindung von Personalbedarf und -ausstattung) vor allem eine Allokations- (Zuordnung von Arbeitskräften zu Allokationsobjekten) und eine Kompensationsfunktion (Ausgleich von Personalbedarfsschwankungen) verbunden.
Neben diesen drei Funktionen lassen sich vier Dimensionen der Personaleinsatzplanung unterscheiden: Hinsichtlich der quantitativen Dimension ist über geeignete Planungen der Einsatz der benötigten Anzahl an Arbeitskräften zu gewährleisten. Die qualitative Dimension betreffend ist der Personalbedarf mit der Personalausstattung abzustimmen, wobei Bedarfe und Ausstattungen nach verschiedenen Kategorien differenziert sein können. In Betracht kommen dabei neben Anforderungsarten (Bedarfsseite) und Qualifikationsarten (Ausstattungsseite) weitere Differenzierungskriterien, wie z.B. Seniorität, Geschlecht o.Ä. Bezüglich der lokalen Dimension geht es um die Zuordnung von Arbeitskräften zu Orten betrieblicher Leistungserstellung wie z.B. Niederlassungen, hierarchischen Rängen oder Sektoren. Hinsichtlich der temporalen Dimension sind den Arbeitskräften Dienstpläne für limitierte Zeiträume zuzuordnen.
II. Ziele der Personaleinsatzplanung
Die bei der Planung des Personaleinsatzes verfolgten Ziele lassen sich hinsichtlich ihres Inhalts (a), hinsichtlich des angestrebten Zielausmaßes (b) und hinsichtlich des verwendeten Messniveaus (c) differenzieren.
Ad (a): Mit der Planung des Personaleinsatzes werden (wie in allen anderen betrieblichen Funktionsbereichen auch) Substanz- und Formalziele verfolgt. Während Substanzziele den Inhaltsaspekt eines Sachproblems betreffen, beschreiben Formalziele über substanzielle Tauglichkeitsaspekte hinausgehende Auswahlkriterien. Die Substanzziele der Personaleinsatzplanung liegen in der Erfüllung der o.g. Funktionen der Konnexion, Allokation und Kompensation. Zur Auswahl von Personaleinsatzplänen werden jedoch Formalziele benötigt, die aus der Perspektive des Betriebes darin liegen, ökonomischen Erfolg zu erzielen. Aus Sicht des Personals hingegen soll die Zufriedenheit der Arbeitskräfte erreicht werden. Die Operationalisierung solcher Formalziele ist aber nicht nur aufgrund der einschlägigen Datenerfassungs-, Amalgamations- und Prognoseprobleme, sondern vor allem auch wegen der korrespondierenden Zurechnungsproblematik häufig ein schwieriges Unterfangen. Sofern es nicht gelingt, den jeweiligen Personaleinsatzentscheidungen auf Seiten des Betriebes konkrete Erlös-, Deckungsbeitrags-, Rentabilitäts- oder Kostenkoeffizienten (u.Ä.) bzw. auf Seiten der Mitarbeiter konkrete Zufriedenheitskoeffizienten zuzuordnen, ist man auf die Verwendung geeigneter Ersatzkriterien angewiesen. Als Ersatzgrößen für die Zufriedenheit der Arbeitskräfte werden dann vielfach Neigungsgradkoeffizienten und als Indikatoren für den wirtschaftlichen Erfolg werden oft Eignungskoeffizienten in Ansatz gebracht, wobei letztgenannte auf summarischen oder analytischen Vergleichen von Anforderungs- und Fähigkeitsprofilen beruhen (Kossbiel, 1992, Sp. 1656 ff.).
Ad (b): Im Rahmen der Personaleinsatzplanung können mit Extremierungs-, Satisfizierungs-, Fixierungs- und Approximierungszielen grundsätzlich vier Zielarten verfolgt werden. Während Extremierungsziele auf die Optimierung der jeweiligen Zielkriterien abstellen, werden bei der Verfolgung von Satisfizierungszielen zufriedenstellende Lösungen gesucht. Über Fixierungs- bzw. Approximierungsziele hingegen strebt man eine exakte bzw. näherungsweise Erreichung der Zielkriterien an. Die Maximierung der Eignungs- oder Neigungsgradsumme, die Minimierung der Personaleinsatzkosten, die Einhaltung von Untergrenzen für die Eignung alloziierter Arbeitskräfte, die exakte Einhaltung von Personalkostenbudgets und die ungefähre Deckung des Personalbedarfs in Toleranzbereichen stellen typische praxisrelevante Beispiele für diese Zielarten dar.
Ad (c): Die Möglichkeiten einer rationalen Gestaltung von Personaleinsatzplänen hängen maßgeblich davon ab, inwieweit die erforderliche Datenbasis bzgl. Zielen und Restriktionen erfasst, präzisiert bzw. konkretisiert werden kann. Es geht also darum, auf welchem Niveau die jeweiligen Daten und Datenrelationen gemessen werden. Im Kontext der Personaleinsatzplanung ist letztlich darauf zu achten, dass alternative Personalzuordnungen hinsichtlich ihrer Zielbeiträge in eine Rangfolge zu bringen sind, sodass nominalskalierte (d.h. die Rangfolge vernachlässigende Daten) nicht in Betracht kommen und lediglich Daten höherer Skalenniveaus in Ansatz zu bringen sind. Da jedoch arithmetische Operationen bei ordinalskalierten Merkmalen unzulässig sind, sollten die Zielkoeffizienten möglichst auf Kardinalskalenniveau angesiedelt sein, um hinreichende Präzision des Planungsergebnisses zu gewährleisten. Sofern eine direkte Messung der Effizienz potenzieller Personaleinsatzentscheidungen durch verhältnisskalierte Kriterien (wie z.B. Deckungsbeiträge oder Kosten) unmöglich erscheint, ist es folglich ratsam, auf intervallskalierte Eignungs- oder Neigungsgrade zurückzugreifen.
III. Modellansätze zur Personaleinsatzplanung
1. Grundmodell der Personaleinsatzplanung
In den letzten fünf Jahrzehnten wurde eine kaum überschaubare Fülle an Modellansätzen zur Personaleinsatzplanung entwickelt, deren Vielfalt wir hier in keiner Weise referierend gerecht werden können. Wir wollen deshalb zunächst ein relativ einfaches, aus der Klasse der ganzzahligen Programmierungsansätze stammendes Grundmodell der Personaleinsatzplanung formulieren, das eine Skizzierung der mannigfaltigen Variationen zum Thema ermöglicht und für das folgende Symbole benötigt werden:


Mit diesen Symbolen lässt sich der gesuchte Ansatz wie folgt formulieren:
Zielfunktion:
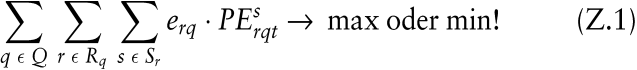
Restriktionen:
Abstimmung von Personalbedarf und Personaleinsatz:
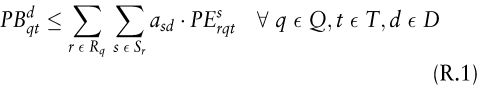
Abstimmung von Personaleinsatz und Personalausstattung:
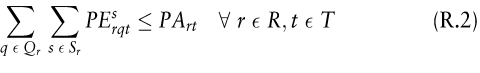
Variablenbedingungen:
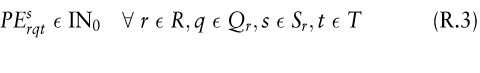
Die Zielfunktion des Modells (Z.1) ist entweder zu maximieren oder zu minimieren und strebt je nach verwendetem Zielkriterium die (jeweils einsatzabhängigen) minimalen Personalkosten, Deckungsbeiträge, Eignungs- oder Neigungsgradsummen o.Ä. an. Über Restriktion (R.1) wird gewährleistet, dass die nach Tätigkeiten, Tagen und Tagesabschnitten differenzierten Personalbedarfe durch den Einsatz hinreichend geeigneter Arbeitskräfte gedeckt werden, während Restriktion (R.2) garantiert, dass nicht mehr Arbeitskräfte zum Einsatz in Leistungsprozessen vorgesehen werden als in der (nach Tagen und Qualifikationsarten differenzierten) Personalausstattung zur Verfügung stehen. Die verwendeten Personaleinsatzvariablen steuern jeweils die Zuordnung der Arbeitskräftearten zu Einsatztagen, Schichten und Tätigkeitskategorien. Daneben wird über die Variablenbedingung (R.3) deren Nichtnegativität und Ganzzahligkeit gefordert.
Dieser Modellansatz ist vielfältigen Variationsmöglichkeiten zugänglich, von denen wir einige im Folgenden ansprechen wollen:
| - | Durch Verwendung zusätzlicher Variablen für die Schulung und die Ausleihe von Personal sowie durch die Integration entsprechender Restriktionen lassen sich die beiden anderen o.g. Alternativen des Personaleinsatzes leicht in Ansatz bringen (Kossbiel, 1988, S. 1095). | | - | Verzichtet man auf die Schichtindices s und ersetzt man die Indices für die Tätigkeiten q durch Stellenindices, geht das Modell in einen Ansatz der Stellenzuweisung über (Spengler, 1993, S. 95 ff.). | | - | Bringt man die Personalbedarfe und/oder die Personalausstattungen nicht als vorgegebene (Daten), sondern als entscheidungsabhängige (Variablen) Größen in den Ansatz ein, wird das vorliegende Modell der konjunkten Personaleinsatzplanung in ein Modell disjunkter Personaleinsatzplanung transformiert (Kossbiel, 1992, Sp. 1661 ff.). | | - | Bei Verzicht auf die Variablen 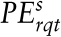 , gleichzeitiger Verwendung entscheidungsabhängiger Personalbedarfe oder -ausstattungen und mit geeigneten Variationen der Zielfunktion wird aus dem Modell einer expliziten ein Modell der impliziten Personaleinsatzplanung (Kossbiel, 1992, Sp. 1660 f.). , gleichzeitiger Verwendung entscheidungsabhängiger Personalbedarfe oder -ausstattungen und mit geeigneten Variationen der Zielfunktion wird aus dem Modell einer expliziten ein Modell der impliziten Personaleinsatzplanung (Kossbiel, 1992, Sp. 1660 f.). | | - | Verknüpft man die Personaleinsatzvariablen über die Teilperioden, dann geht das oben formulierte statische Modell in einen dynamischen Ansatz über (Kossbiel, 1992, Sp. 1663 ff.). | | - | Durch Formulierung mehrerer Teilzielfunktionen (z.B. zur Kostenminimierung und Neigungsgradmaximierung) erhalten wir ein Vektoroptimierungsmodell, das mit den gängigen Verfahren (wie z.B. Ansätzen des Goalprogramming, klassischen Nutzenmodellen oder fuzzy set-basierten Verfahren) gelöst werden kann (Spengler, 1993, S. 34 ff.). |
2. Modellansätze zur Dienstplanung
Das Problem der Dienstplanung stellt ein zentrales Problem der Personaleinsatzplanung dar und tritt in allen Betrieben auf, in denen die individuelle Arbeitszeit der Beschäftigten von der Betriebszeit des Unternehmens abweicht. Die Modellansätze zur Dienstplanung werden in der Literatur vielfach wie folgt differenziert (Günther, 1989, S. 211 f.; Salewski, 1998, S. 129 ff.; Strauß, 2001, S. 26 ff.; Weber, 1997, S. 30 f.): Über Ansätze des sog. Days Off Scheduling, auf die wir unten ausführlicher eingehen wollen, werden den Arbeitskräften je nach Festlegung des Planungszeitraumes (z.B. wochen-, monats- oder quartalsweise) Arbeitstage und arbeitsfreie Tage zugeordnet. Modelle des sog. Shift Scheduling sind häufig auf einen singulären Tag bezogen und thematisieren die Allokation von konsekutiven Schichtmustern zu Arbeitskräften, während über das sog. Tour Scheduling den Mitarbeitern Dienste mit differierenden (sich z.T. überschneidenden) Beginn- und Endzeitpunkten zugewiesen werden.
Zur Lösung von Days Off Scheduling-Problemen wird in der Literatur eine Fülle (situations)spezifischer Algorithmen angeboten (Nanda, /Browne, 1992, S. 85 ff.). Für Fälle, in denen die Personalbedarfe und -ausstattungen homogen sind, in denen Personalbedarfsüber- im Gegensatz zu -unterdeckungen zulässig sind, und in denen alle Arbeitskräfte (nach lediglich einem Schichtgrundmuster) an mehreren Tagen arbeiten und dann en bloc frei haben (z.B. 6 Tage Arbeit, 3 Tage frei), ist das sog. First Period Principle (FPP) von Nanda/Browne (Nanda, /Browne, 1992, S. 94 ff.) ein gut geeignetes (optimierendes) Lösungsverfahren. Wir wollen diesen Algorithmus anhand eines einfach gehaltenen Beispiels erläutern, in dem montags, dienstags, donnerstags und samstags je 9, mittwochs 2, freitags keine und sonntags 4 Arbeitskräfte benötigt werden und die Arbeitskräfte an je 5 aufeinanderfolgenden Tagen Dienst und an 2 zusammenhängenden Tagen frei haben. Der Algorithmus umfasst die folgenden sieben Schritte:
| - | Liste die täglichen Personalbedarfe auf! | | - | Setze genügend Arbeitskräfte zur Deckung der täglichen Personalbedarfe ein! Berücksichtige dabei bereits an Vortagen eingesetzte Arbeitskräfte, für die am jeweiligen Tag noch ein Einsatz vorgesehen ist! | | - | Fahre mit der Zuordnung solange nach 2. fort, bis sich die Zuordnungsmuster wiederholen (s. Tab. 1)! 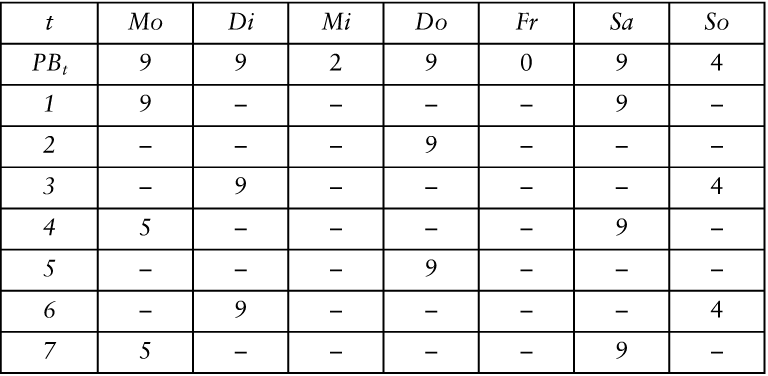 Tab. 1: Schritte 1 – 3 im FPP [Hinweis: Das sich wiederholende Zuordnungsmuster besteht aus den in den Zeilen 2 – 4 aufgeführten Allokationen.]
| | - | Bilde für jeden Wochentag das arithmetische Mittel (AM) über die sich wiederholenden Zuordnungsmuster (s. Tab. 2)!  Tab. 2: Schritt 4 im FPP
| | - | Bilde für jeden Wochentag zunächst die kumulierte Summe der Durchschnittswerte (KS) und runde diese dann auf die nächsthöhere ganze Zahl (INT) (s. Tab. 3)!  Tab. 3: Schritt 5 im FPP
| | - | Subtrahiere den kumulierten Wert des Vortages (INT_V) vom kumulierten Wert des betrachteten Tages (INT), um die Anzahl der an diesem Tag mit dem Dienst beginnenden Arbeitskräfte zu ermitteln (s. Tab. 4)! 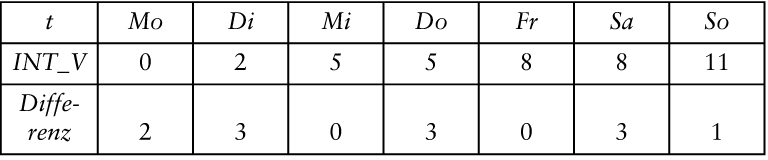 Tab. 4: Schritt 6 im FPP
| | - | Notiere den Einsatzplan (s. Tab. 5)! |
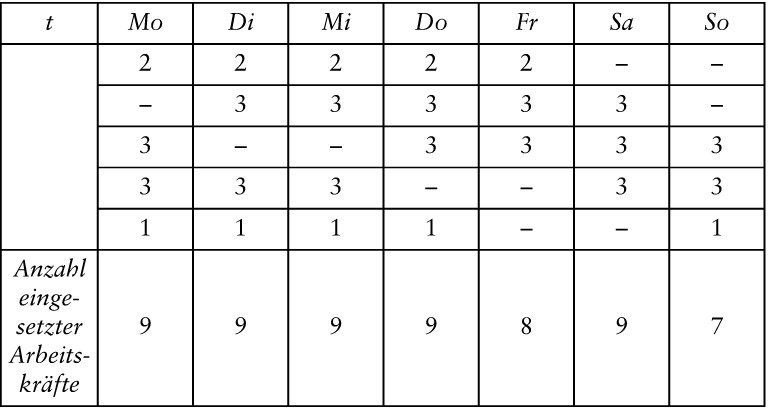
Tab. 5: Schritt 7 im FPP
Als Ergebnis erhalten wir somit einen (optimalen) Dienstplan, bei dem die Personalbedarfe für Montag, Dienstag, Donnerstag und Samstag exakt gedeckt und am Mittwoch Überdeckungen in Höhe von 7, freitags in Höhe von 8 und sonntags in Höhe von 3 Arbeitskräften eingeplant werden.
3. Modellansätze für Unsicherheits- und Unschärfesituationen
Viele Modellansätze zur Personaleinsatzplanung basieren auf der Annahme, dass der Entscheidungsträger die für das Modell benötigten Daten und Relationen sowie die erforderliche Regelbasis präzise angeben kann. Solche Ansätze sind für Unbestimmtheitssituationen, d.h. für Situationen, in denen der Eintritt künftiger Ereignisse unbestimmt und damit unsicher oder die Ereignisse selbst unbestimmt und damit unscharf sind, ungeeignet.
In Fällen der Unsicherheit, in denen die Datenbasis in Form stochastischer Größen vorliegt (sog. Risikosituationen), lassen sich zur Lösung des unter III.1. formulierten Grundmodells (einschl. Varianten) Ansätze der stochastischen Programmierung, wie z.B. die Fat Solution-Methode, Modelle des Chance Constrained-Programming, Zwei-Stufen-Kompensations- oder Erwartungswertmodelle heranziehen (Jarr, 1976; Spengler, 1999, S. 84 ff.).
In der Wirtschaftspraxis ist man häufig nicht in der Lage, die erforderlichen Personalbedarfe, Kostenkoeffizienten, Produktivitätskennziffern, Eignungsgrade u.v.m. exakt (sondern lediglich größenordnungsmäßig) anzugeben. Auch werden vielfach unscharfe Regeln für die Komposition von Personaleinsatzplänen verwendet, z.B. wenn möglichst zusammenhängende freie Tage gewährt (Muche, 1995), Personalbedarfe möglichst gut gedeckt oder Einsatzpläne möglichst gerecht gestaltet werden sollen. Für solche Unschärfesituationen werden in jüngster Zeit modellgestützte Lösungsprozeduren entwickelt, die auf unscharfen Regelungsmechanismen und somit auf Verfahren des sog. Fuzzy Control basieren. Diese neueren Ansätze sind nicht nur in der Lage, unscharfe Daten und Relationen mathematisch exakt zu verarbeiten, sondern sie stellen auch einen vielversprechenden Weg dar, das vielfach bei Ansätzen der mathematischen Programmierung gravierend auftretende Lösbarkeitsproblem wesentlich abzuschwächen (Jaanineh, /Maijohann, 1996, Kahlert, /Frank, 1993, Kieper, /Spengler, 2002, S. 78 ff.; Schroll, /Spengler, 2002).
IV. Kritische Würdigung
Der vorliegende Beitrag ist Grundlagen und Modellansätzen der Personaleinsatzplanung gewidmet. Dieser Planungsbereich umfasst viele interessante und in der Wirtschaftspraxis Problemdruck erzeugende Facetten, von denen einige hier aufgrund einer engen Seitenrestriktion nicht oder nur andeutungsweise angesprochen werden. Wir wollen deshalb abschließend konstatieren, dass Problemstellungen der Personaleinsatzplanung durchgängig in mathematischen Programmierungsmodellen erfasst, diese jedoch häufig aufgrund der obwaltenden Ganzzahligkeitsbedingungen sowie des hohen Modellumfangs nicht (oder nicht in hinreichender Zeit) gelöst werden können (Grötschel, /Lovász, /Schrijver, 1988). Die wissenschaftliche Forschung ist daher aufgefordert, sich verstärkt mit der Entwicklung regelbasierter Modelle und Lösungsprozeduren zu beschäftigen.
Literatur:
Grötschel, M./Lovász, L./Schrijver, A. : Geometric Algorithms and Combinatorial Optimization, Berlin et al. 1988
Günther, H. O. : Produktionsplanung bei flexibler Personalkapazität, Stuttgart 1989
Jaanineh, G./Maijohann, M. : Fuzzy-Logik und Fuzzy-Control, Würzburg 1996
Jarr, K. : Stochastische Personalplanungen, Diss., Hamburg 1976
Kahlert, J./Frank, H. : Fuzzy-Logik und Fuzzy Control. Eine anwendungsorientierte Einführung, Braunschweig et al. 1993
Kieper, F./Spengler, T. : Das 3-Säulen-Personalmanagement und Fuzzy-Control, in: Der Controlling-Berater, H. 3/2002, S. 69 – 88
Kossbiel, H. : Personalbereitstellung und Personalführung, in: Allgemeine Betriebswirtschaftslehre, hrsg. v. Jacob, H., 5. A., Wiesbaden 1988, S. 1045 – 1253
Kossbiel, H. : Personaleinsatz und Personaleinsatzplanung, in: Handwörterbuch des Personalwesens, hrsg. v. Gaugler, E./Weber, W., 2. A., Stuttgart 1992, Sp. 1645 – 1666
Muche, G. : Dienstplanung. Planung und Verwaltung des Personaleinsatzes im Gastgewerbe, Hamburg 1995
Nanda, R./Browne, J. : Introduction to Employee Scheduling, New York 1992
Salewski, F. : Klassifikation von Dienstplanungsproblemen, in: Modellgestützte Personalentscheidungen 2, hrsg. v. Kossbiel, H., München, Mering 1998, S. 119 – 136
Schroll, A./Spengler, T. : Fuzzy Control in der Personaleinsatzplanung, in: Modellgestützte Personalentscheidungen 6, hrsg. v. Kossbiel, H./Spengler, T., München, Mering 2002, S. 121 – 140
Schweitzer, M. : Planung und Kontrolle, in: Allgemeine Betriebswirtschaftslehre Band 2, hrsg. v. Bea, F. X./Dichtl, E./Schweitzer, M., 3. A., Stuttgart et al. 1987, S. 9 – 72
Spengler, T. : Grundlagen und Ansätze der strategischen Personalplanung mit vagen Informationen, München et al. 1999
Spengler, T. : Lineare Entscheidungsmodelle zur Organisations- und Personalplanung, Heidelberg et al. 1993
Strauß, C. : Quantitative Personaleinsatzplanung im Airline Business, Frankfurt et al. 2001
Weber, J. : Arbeitszeitflexibilisierung und ihre Berücksichtigung in optimierenden Personalplanungsmodellen – die implizite Bestimmung der täglichen Arbeits- und Pausenzeit unter expliziter Berücksichtigung der rechtlichen Regelungen des Arbeitszeitgesetzes, in: Modellgestützte Personalentscheidungen 1, hrsg. v. Kossbiel, H., München, Mering 1997, S. 29 – 56
|