|
Produktionstheorie, dynamische
Inhaltsübersicht
I. Notwendigkeiten einer dynamischen Betrachtungsweise
II. Formen der Dynamisierung
III. Dynamische Aktivitätsanalyse
I. Notwendigkeiten einer dynamischen Betrachtungsweise
Im bwl. Schrifttum wird eine Fülle von Argumenten angeführt, dass die Beschreibung und Erläuterung praktischer Produktionsvorgänge eine dynamische Betrachtungsweise notwendig macht:
| - | Küpper (Küpper, H.-U. 1980) weist darauf hin, dass die Durchführung von Produktionsprozessen infolge des Beginns, der Dauer, Gang- und Operationsfolge von Arbeitgängen sowie des Bearbeitungsfortschritts Zeit beansprucht. Der Bestand und Einsatz von Arbeitskräften hängt wesentlich von Einstellungs- und Entlassungsentscheidungen in den Vorperioden ab. Aufgrund der Abnutzung im Produktionsprozess nimmt die Produktivität von Anlagen über die Zeit ab, und die Ausschussquote steigt. Nachfrageänderungen beeinflussen das Produktionsprogramm und die Strukturierung des Produktionsprozesses. Und schließlich hält Küpper die Nutzung begrenzter Kapazitäten der Produktiveinheiten, die Mehrstufigkeit von Stückprozessen und die Fertigung in Losen als weitere Indizien dafür, dass solche zeitlichen Interdependenzen zwischen Inputs, Outputs und Produktionsverfahren in die produktionstheoretischen Überlegungen mit aufgenommen werden müssen. | | - | Kistner/Luhmer (Kistner, K.-P./Luhmer, A. 1988) zeigen, dass die Überlegungen, der Verschlechterung der technischen Situation eines Aggregats infolge von Verschleiß durch Wartungs- bzw. Instandhaltungsmaßnahmen zu begegnen, die Formulierung eines dynamischen Modells des Betriebsmitteleinsatzes notwendig machen. | | - | Trossmann (Trossmann, E. 1986) begründet in der mehrstufigen Mehrproduktfertigung die explizite Einbeziehung der Zeit in die Produktionsanalyse durch die Vorlaufzeitverschiebungen der Aufträge bei einer mehrstufigen Bedarfsauflösung. Zeitliche Verlagerungen von Arbeitsgängen durch Kapazitätsbegrenzungen können dazu führen, dass unbearbeitete Vorprodukte oder Zwischenprodukte bis zu ihrer Weiterbearbeitung gelagert werden müssen, wodurch sich Lager- und Wartezeiten ergeben, die einer entsprechenden Behandlung und Erklärung bedürfen. | | - | Einen weiteren Grund für die Notwendigkeit der Formulierung von dynamischen Ansätzen in der Produktionstheorie stellt der technische Fortschritt dar. Er kann in autonomer Form auftreten, wenn die Zeitabhängigkeit von Technologien durch Innovationen begründet ist, die von außen in das Unternehmen hereingetragen werden. Dagegen handelt es sich um induzierten technischen Fortschritt, wenn er auf Lernprozessen basiert, die aus den Unternehmungen selbst heraus angestoßen werden. In jedem Falle aber wird die Produktion durch fallende Produktionskoeffizienten zeitabhängig und damit eine Funktion des Standes der Technik (siehe hierzu z.B. Ihde, G. B. 1970 und Lücke, W. 1976). |
Zusammenfassend kann man also hier sagen, dass sich die Beweggründe und Notwendigkeiten für eine dynamische produktionswirtschaftliche Betrachtungsweise allg. unmittelbar aus den dynamischen Veränderungen heraus ergeben, welche die Elemente einer Produktionstechnologie im Laufe der Zeit erfahren können (Fandel, G. 2005). Elemente einer jeden beliebigen Produktionstechnologie sind aber die Outputs und die Inputs sowie die Produktionsverfahren, die festlegen, welche Input-Output-Kombinationen bzw. Produktionspunkte realisiert werden können, also die Aktivitäten. Sie für die dynamischen Produktionsfälle der Unternehmungen geeignet zu fassen, wäre der methodische Einstieg für eine praktisch verwertbare dynamische Aktivitätsanalyse, die den bislang nur vereinzelt vorliegenden und mitunter sehr heterogenen Ansätzen der dynamischen Produktionstheorie eine einheitliche bzw. gemeinsame Untersuchungsbasis bilden würde. Dafür aus der Unternehmenspraxis passende Anhaltspunkte zu finden, war das Motiv einer empirisch-deskriptiven Analyse von Fandel et al. (Fandel, G./Dyckhoff, H./Reese, J. 1994) über die industrielle Produktionsentwicklung in ausgewählten Branchen.
II. Formen der Dynamisierung
Die bisher in der Literatur vereinzelt vorgetragenen Ansätze einer dynamischen Produktionstheorie schienen Wittmann (Wittmann, W. 1979, S. 277) so verschiedenartig, dass er meinte, es sei wohl »keine dynamische Theorie mit einheitlicher Grundlage als Pendant zur statischen« zu erwarten, »sondern eher verschiedene dynamische Theorien unterschiedlicher Herkunft und mit unterschiedlichen Verfahrensweisen«. Zudem handle es sich bei den vorliegenden Traktaten meist um isolierte Arbeiten, die eher als Sonderfälle anzusehen seien, sodass der statischen Produktionstheorie wohl kein gleichwertiger Konkurrent aus dynamischer Perspektive erwachse. Zu diesem Zeitpunkt war das Buch von Shephard/Färe (Shephard, R. W./Färe, R. 1980) über eine dynamische Theorie der Produktionskorrespondenzen noch nicht erschienen, das die Erkenntnisse der früheren Publikationen Shephard/Färe (Shephard, R. W./Färe, R. 1975) und Shephard et al. (Shephard, R. W./Al-Ayat, R. A./Leachman, R. C. 1977) verallgemeinert, auf die Wittmann (Wittmann, W. 1979) zum Teil seine Behauptung stützte. Bevor jedoch die Möglichkeiten der entsprechenden Axiomatisierung einer aktivitätsanalytisch fundierten dynamischen Produktionstheorie erörtert werden, soll zunächst trotz der vermeintlichen Unverbundenheit versucht werden, die wesentlichen, bereits existierenden Formen einer Dynamisierung systematisch anzusprechen und kurz kritisch zu würdigen. Auf die Unterschiede in der Analyseform, die sich aus einer diskreten oder kontinuierlichen Zeitbetrachtung ergeben – also dadurch, dass man den zeitlichen Produktionsverlauf anhand von Gütermengen und alternativ anhand von Produktionsgeschwindigkeiten der Outputs bzw. Verbrauchsgeschwindigkeiten der Inputs studiert – , soll dabei nicht näher eingegangen werden, obwohl dadurch Änderungen in den Effizienzaussagen notwendig werden könnten. Denn bei gleichen Output- und Inputmengen über die Zeit könnten durchaus die entsprechenden Geschwindigkeiten verschiedenartig zeitlich verteilt sein.
Förstner/Henn (Förstner, K./Henn, R. 1957) formulieren ihren diskontinuierlichen dynamischen Ansatz als mehrperiodige Produktions- und Absatzprogrammplanung, wobei die Dynamik eher über die Absatz- und Beschaffungsseite insofern eingebracht wird, als von in der Zeit veränderlichen Output- und Inputpreisen ausgegangen wird. Die Produktionstechnologie selbst erfährt dagegen keine zeitlichen Veränderungen, sodass hier statische Produktionsbedingungen vorherrschen, die für weitere Überlegungen so nicht sehr fruchtbar sind. In der kontinuierlichen Formulierungsvariante sind die Produktions- und Verbrauchsgeschwindigkeiten dann zwar zeitabhängig, was aber ebenfalls noch keine Dynamik der Produktionsbedingungen bedeuten muss, denn derartige Verhältnisse wären bei variabler Leistungsintensität auch innerhalb der Gutenberg-Produktionsfunktion darstellbar, die jedoch zu den statischen Ansätzen gerechnet werden muss. Lediglich die Einführung eines zusätzlichen Terms für den technischen Fortschritt in die Produktionsfunktion hält in dieser Konzeption noch die Möglichkeiten für dynamische Technologien offen. Eine solche Vorgehensweise deckt sich mit der Formulierung dynamischer Produktionsfunktionen, in denen technologische Produktionsveränderungen mit Qualitätsänderungen der Faktoren identifiziert und durch in der Zeit fallende Produktionskoeffizienten beschrieben werden. Ähnliche Phänomene treten speziell beim Faktor Arbeitskräfte infolge eines durch Lernen in der industriellen Produktion induzierten technischen Fortschritts auf. Hierbei wird im Rahmen der Linearhypothese der Lernkurven häufig unterstellt, dass der Produktionskoeffizient einer bestimmten Personalart mit der Verdopplung der Zahl der hergestellten Produkteinheiten um einen gleich bleibenden prozentualen Betrag fällt (Baur, W. 1967). Das ist eine explizit zum Ausdruck gebrachte Zeitinterdependenz von Inputs und Outputs verschiedener Produktionsperioden, die als Beschreibungselement einer dynamischen Produktionsfunktion gelten kann. Dies leitet über zu einer zweiten Gruppe von Ansätzen, die solche Zeitinterdependenzen in allg. Form betrachtet.
Küpper (Küpper, H.-U. 1979) hat auf der Basis des Input-Output-Ansatzes eine allg. dynamische Produktionsfunktion formuliert, welche die Beschreibung der zeitlichen Entwicklung von Gütereinsatz, Fertigungszeiten und Güterausbringung und die Verbindung von produktionstheoretischen und ablauforganisatorischen Tatbeständen der Fertigung ermöglichen soll. Speziell unter dem ersten Aspekt bringt die dynamische Produktionsfunktion die Beziehungen zwischen den Gütermengen und ihrer Verwendung für den Absatz oder für Lagerbestandsveränderungen zum Ausdruck. Je nach der Verweildauer der Einsatzgüter in den Teilprozessen der mehrstufigen Fertigung wird dabei den zeitlich unterschiedlich gestuften Produktionsvorgängen wahlweise durch die statische oder dynamische Formulierung von Transformationsfunktionen Rechnung getragen. Nichtnegativitätsbedingungen, Kapazitätsrestriktionen und Bilanzgleichungen der Produktion treten ergänzend hinzu.
Der Ansatz von Stöppler (Stöppler, S. 1975) ist stärker auf die Klärung der Frage gerichtet, wie sich ökonomische Entscheidungen über die Produktionstechnologie eines Unternehmens zu früheren Zeitpunkten auf die produktionstechnologischen Möglichkeiten des Unternehmens zu späteren Zeitpunkten auswirken können und wie man diese Einflüsse und Zusammenhänge in geeigneter Weise erfasst. Kernelemente des sich der Systemtheorie bedienenden dynamischen Produktionssystems von Stöppler sind Technologie-, Kontroll-, Ziel-, Produktions- und Übergangsgleichungen, wobei die hier insb. interessierende Technologiegleichung Veränderungen der Technologiemenge im Zeitablauf ausdrückt. Diese Vorgehensweise besitzt den Vorteil, technologische Wandlungen einer Unternehmung umfassender zu erklären, scheitert aber in aller Regel am Komplexitätsgrad des Beschreibungsmodells. Das gilt erst recht dann, wenn z.B. mithilfe der Variationsrechnung alle Produktionsmöglichkeiten zum Zeitpunkt t ermittelt werden sollen, die infolge der Entwicklung aller zulässigen Produktionssysteme denkbar sind. Hinzu kommt ein weiterer methodischer Vorbehalt. Dynamische Aktivitäten sind i.A. so zu spezifizieren, dass sie sich über einen Zeitraum erstrecken und nicht nur auf einen Zeitpunkt beziehen. Dann ist aber die Charakterisierung einer Technologie T zum Zeitpunkt t allein durch die Güterkomponenten in t insofern wieder eine unbefriedigende Verkürzung, als diese Technologie eigentlich ausdrücken soll, welche Aktivitäten dem Unternehmen im Zeitpunkt t aufgrund seines technischen Wissens zur Realisierung zur Verfügung stehen.
Eine derart wünschenswerte Erweiterung des Technologiebegriffs wird in den am weitesten vorangetriebenen Konzepten einer dynamischen Aktivitätsanalyse von Malinvaud (Malinvaud, E. 1953) und Shephard/Färe (Shephard, R. W./Färe, R. 1980) vorgetragen. Auf sie wird im Folgenden noch näher eingegangen. Insb. das Letztere der beiden Konzepte scheint mit einigen simplen Modifikationen am ehesten unmittelbar dafür geeignet zu sein, dynamische Produktionen in Unternehmungen praxisadäquat zu erfassen und in eine handhabbare Formulierung zu bringen sowie als gemeinsame Basis der zuvor angesprochenen Dynamisierungsformen zu fungieren; sie stellen dann explizit ausgedrückte Spezialfälle einer impliziten Beschreibung der dynamischen Produktionsvorgänge dar, wie es analog in der statisch-deterministischen Situation der Fall ist.
May (May, E. 1992) hat mit seiner Arbeit einen wichtigen Schritt in dieser Richtung getan, indem er die aktivitätsanalytische Betrachtung dynamischer Input-Output-Modelle der Produktion mit dem Konzept im Zeitablauf veränderlicher Transformationsfunktionen und dem Verfahren der Diagonalmatrizenmultiplikation verknüpft, um evolutorische Produktionszusammenhänge über mehrere Perioden hinweg zu modellieren und zu beschreiben. Diese Ergebnisse haben dazu angeregt, die axiomatische Fundierung der dynamischen Produktionstheorie weiterzuentwickeln.
III. Dynamische Aktivitätsanalyse
1. Der Ansatz von Malinvaud
Der Ansatz von Malinvaud (Malinvaud, E. 1953) bezieht sich ursprünglich auf eine volkswirtschaftliche Problematik, kann aber ohne weiteres aus bwl. Perspektive entsprechend verstanden werden. Es geht um die Frage, wie die Produktion zeitlich verteilt sein soll, damit ein Produktionsplan mit maximalem Gegenwartswert herauskommt. Lässt man die Bewertung außen vor, da sie aus produktionstheoretischer Sicht unerheblich ist, dann ist ein solcher Produktionsplan eine Aktivität des Unternehmens über alle zukünftigen Perioden hinweg bis ins Unendliche, deren Menge von Malinvaud als Chronik bezeichnet wird. Dabei lässt sich die Aktivität als eine Folge von Produktionsvektoren spezieller Art auffassen, die aus Teilvektoren für Güterbestände bt, Güterentnahmen et, Güterweiterverwendungen r?t, Güterzuführungen r^t von außerhalb des Unternehmens, Gütereinsatzmengen rt und daraus hergestellten Gütermengen bt+1 zusammengesetzt sind (Abb. 1; Wittmann, W. 1979). Eine solche Sichtweise schließt die Lagerhaltung, Investition und Desinvestition mit ein. Produktionsprozesse finden jeweils stets nur mit einem einperiodigen Verzug von einer Vorperiode zur unmittelbar nachfolgenden Zeitperiode statt. Die Zeit wird im Modell als diskrete Größe behandelt.
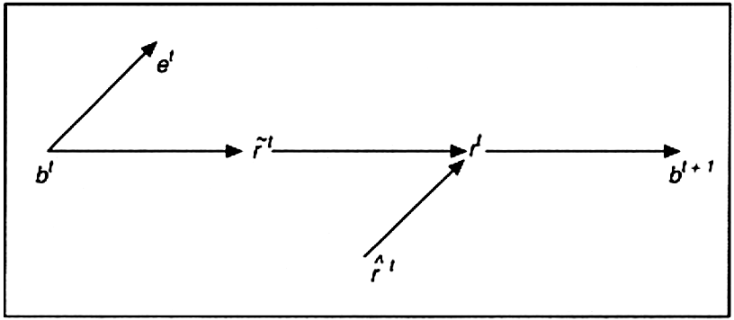
Abb. 1: Wirkungsbeziehungen bei einem einperiodigen Verzug
Der Ressourcenvektor r^t unterliegt Obergrenzen der Verfügbarkeit. Fasst man die Produktionsaktivität im Zeitpunkt t zusammen als vt = (-rt,bt+1)\', rt ≥ 20, dann wird die Technologiemenge Tt definiert als
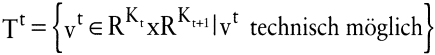
mit RKt als reellwertigem Güterraum zum Zeitpunkt t. Für eine Chronik C gilt dann
C = {v ∊ R | v = v1, v2, ?,vt, ? ) und
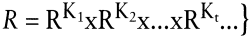 . .
Eine solche Chronik bzw. ihre Aktivitäten werden naturgemäß durch ein System von Mengenbilanzen über die Zeit begleitet, wobei man im Zeitpunkt t
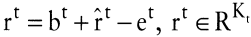 , ,
bzw. allgemein
r = b + r^ – e, r ∊ R,
mit r = (r1,r2, ?,rt, ?) und b, r^ bzw. e entsprechend hat.
Abgesehen von einzelnen vwl. Erklärungsschwächen dieses Ansatzes gibt es aus bwl.-produktionstheoretischer Sicht im Wesentlichen zwei Kritikpunkte an der Bildung von Chroniken bzw. den damit zusammenhängenden Technologien. Erstens sind Aktivitäten mit einem unendlichen Zeithorizont aus praktischer Sicht wenig brauchbar, da die Auswirkungen von Entscheidungen im Produktionsbereich i.d.R. zeitlich beschränkt sind. Dies verlangt nach einer praktisch plausibleren begrifflichen Fassung von dynamischen Aktivitäten. Zweitens ist die Beschreibung von Produktionsvorgängen jeweils durch die Input-Output-Vektoren nur zweier unmittelbar aufeinander folgender Perioden zu speziell, als dass sie bei unterschiedlichen Verweilzeiten einer mehrstufigen Fertigung mit Zwischenprodukten befriedigen könnte. Normalerweise erstrecken sich derartige Produktionsprozesse auf mehr als nur zwei Zeitperioden. Ein Kompromiss, der gleichermaßen beiden Kritikpunkten in gewisser Weise Rechnung zu tragen versucht, könnte darin bestehen, dynamische Technologien als Mengen von mehrperiodigen, zeitlich begrenzten Aktivitäten zu begreifen. Bevor eine solche Modifikation durchgeführt wird, soll zunächst noch auf die wesentlichsten Gedanken von Shephard/Färe (Shephard, R. W./Färe, R. 1980) zur Behandlung dynamischer Technologien bzw. Korrespondenzen eingegangen werden. Abwandlungen und Vereinfachungen dieser Überlegungen finden sich in Shephard et al. (Shephard, R. W./Al-Ayat, R. A./Leachman, R. C. 1977), Shephard (Shephard, R. W. 1983) und Färe (Färe, R. 1988). Sie geben Einblick in die Möglichkeiten der axiomatischen Begründung von dynamischen Technologien.
2. Der Ansatz von Shephard/Färe
In dem Ansatz von Shephard/Färe (Shephard, R. W./Färe, R. 1980) wird die Zeit als stetige Größe behandelt. Die Autoren definieren
r = r(t), t ∊ [0,+∞),
als einen Vektor der zeitlichen Historie von Inputgeschwindigkeiten und entsprechend
x = x(t), t ∊ [0,+∞),
als Vektor der zeitlichen Historie von Outputgeschwindigkeiten. Dann ist eine dynamische Outputkorrespondenz eine Abbildung
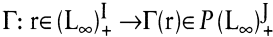
wobei Γ(r) die Teilmenge der Vektoren von zeitlichen Historien von Outputgeschwindigkeiten ist, die mit dem Vektor r der zeitlichen Historie von Inputgeschwindigkeiten erreicht werden kann. (L∞)+I bzw. (L∞)+J* sind die zeitlich unendlichen, positiven Räume der Vektoren der Input- und Outputgeschwindigkeiten. P steht für das Symbol der Potenzmengen. Die Outputmengen Γ(r) werden den folgenden Axiomen unterworfen:


Zwei weitere Axiome treten plausiblerweise noch hinzu, welche die zeitliche Verteilung der Outputhistorie betreffen. Sei v? = (x,r)′ und
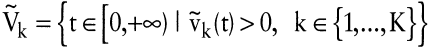 , ,
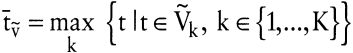 , ,
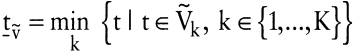 , ,
dann gelte weiterhin
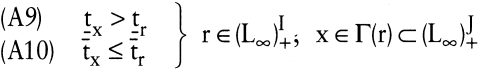 , ,
(A9) fordert, dass es Zeit dauert, bis aus Inputs Outputs werden; (A10) impliziert, dass es weiter keinen Output mehr gibt, wenn kein Input mehr eingesetzt wird.
Die Axiome können analog für dynamische Inputkorrespondenzen
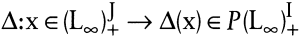
formuliert werden, wobei Δ(x) eine Teilmenge von zeitlichen Historien von Verbrauchsgeschwindigkeiten der Inputs ist mit
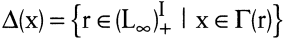
Shephard/Färe (Shephard, R. W./Färe, R. 1980) beweisen die Widerspruchsfreiheit und Unabhängigkeit dieser Axiome. Sei nun
T = {v = (x,-r)′ | x ∊ Γ(r), r ∊ Δ(x)} ⊂ (L∞)K
die dynamische Technologiemenge, die aus der Menge aller Vektoren von zeitlichen Historien der Output- und Inputgeschwindigkeiten besteht, und
Te = {v ∊ T | w ∊ T∧ w≥v→v=w} ⊂ T
die Teilmenge der effizienten Historien, dann sei f: (L∞)K →R eine dynamische Produktionsfunktion genau dann, wenn gilt
f(v) = f(v(t)) = f((x(t),-r(t))′) = 0, t ∊ [0,+∞), ↔ v∊Te.
Die Relation w ≥ v in der Definition von Te sei dabei verstanden als
w ≥ v ↔ wk(t) ≥ vk(t) für alle k ∊ {1, ?, K} und alle t ∊ [0,+∞).
Erweiterungen dieser Axiomatik um zusätzliche Annahmen, wie z.B. die Verteilung eines Ressourcenbudgets über die Zeit, machen diese Analyse unmittelbar verwertbar für die Produktionsplanung komplizierter Erzeugungsprozesse; Shephard et al. Shephard, R. W./Al-Ayat, R. A./Leachman, R. C. 1977) und Shephard (Shephard, R. W. 1983) führen das explizit am Fallbeispiel des Schiffbaus aus. So brillant diese vorgetragene Axiomatisierung dynamischer Technologien bzw. Produktionskorrespondenzen von den Autoren auch zweifelsohne konzipiert worden ist, sie weist dennoch aus praktischer Sicht eine erhebliche Schwäche auf, die aus der Diskussion des Ansatzes von Malinvaud (Malinvaud, E. 1953) bekannt ist: Dynamische Aktivitäten bzw. Input-Output-Historien zu einem Zeitpunkt t = 0 entwickeln sich i.d.R. nicht zeitlich ins Unendliche weiter, sondern sind üblicherweise in ihren zeitlichen Auswirkungen beschränkt. Vorteilhaft ist dagegen im Vergleich zu Malinvaud (Malinvaud, E. 1953), dass die Historien hinsichtlich der realen Erzeugungsvorgänge mehr als nur zwei unmittelbar aufeinander folgende Perioden umfassen können. Wie die zuvor monierte Schwäche durch Modifikation bzw. andere Spezifizierungen dynamischer Aktivitäten (Fandel, G. 1990) behoben werden kann, soll im Folgenden gezeigt werden, wobei die Zeit als diskrete Größe behandelt wird. Einer Umformulierung auf den stetigen Fall steht prinzipiell nichts entgegen.
3. Ein modifizierter Ansatz
Eine dynamische Aktivität zum Zeitpunkt t sei als eine begrenzte zeitliche Folge von Input-Output-Vektoren der Form
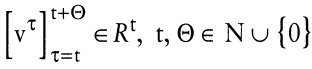 , ,
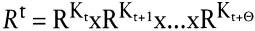
definiert, wobei Θ die maximale Anzahl von Perioden angibt, über die hinweg sich noch Auswirkungen in der Produktion eines Unternehmens bei der Wahl dieser Aktivität ergeben können, d.h. es soll gelten
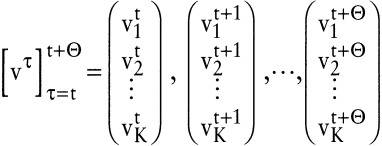
Für Θ = 3 hieße das z.B., dass eine Aktivität, die man zum Zeitpunkt t wählen kann, vier Perioden später und danach keinen Effekt auf die Produktionssituation des Unternehmens mehr hat. Das entspricht u.a. der Tatsache endlicher Verweilzeiten von Gütern bis zur Fertigstellung der Produkte, begrenzten Verteilungsmustern von Ressourcenbeständen über die Zeit bzw. einer beschränkten Lebenszeit von Maschinen sowie einer allg. schlechthin maximalen Verfügbarkeitszeit an Betriebsmitteln.
Seien
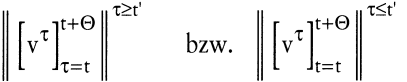
mit t ≤ t′ ≤ t + Θ,
die Teilfolgen der Folge 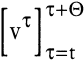 , die auf die Glieder τ ≥ t′ bzw. τ ≤ t′ eingeschränkt sind, dann sei die dynamische Technologie Tt,Θ zum Zeitpunkt t mit der Wirkungsreichweite Θ definiert durch , die auf die Glieder τ ≥ t′ bzw. τ ≤ t′ eingeschränkt sind, dann sei die dynamische Technologie Tt,Θ zum Zeitpunkt t mit der Wirkungsreichweite Θ definiert durch
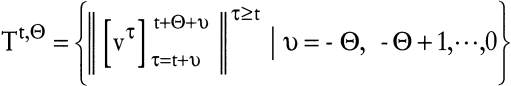 . .
Für υ ≠ 0 kann man sich die Teilfolgen mit weniger als Θ+1 Gliedern durch Glieder, die jeweils aus dem Nullvektor bestehen, aufgefüllt vorstellen. Diese Teilfolgen fangen die Auswirkungen, die Aktivitäten aus zeitlich vorgelagerten Technologien Tt+υ,Θ noch auf die Technologie Tt,Θ haben, mit ein. Das sind die Konsequenzen vergangener Entscheidungen in der Produktion, die – auch bei sonstigem Nichtstun – insofern noch als Aktivitäten der Technologie zum Zeitpunkt t mit zu berücksichtigen sind, als sie entweder sinnvollerweise zu Ende geführt werden müssen oder über ihren Abbruch noch zu entscheiden ist.
Neben den üblichen Anforderungen an Technologien bzw. deren Elemente sollen an die Folgen, die zur Technologie Tt,Θ gehören, noch die nachstehenden Bedingungen gestellt sein.

Die strukturellen Zusammenhänge seien durch Abb. 2 für Θ = 3 skizziert. Die Pfeile stellen Reichweiten von Folgen oder Teilfolgen dar, die zur Technologie Tt,3 gehören.
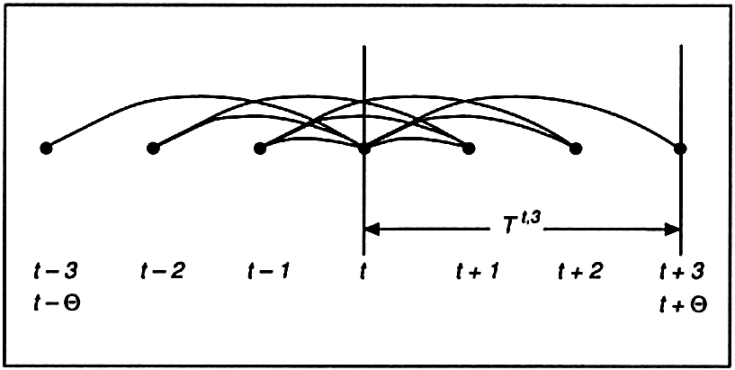
Abb. 2: Dreiperiodige Wirkungsbeziehungen der Technologie T t, 3
Die Menge 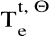 der effizienten Produktionsvektorfolgen bzw. die dynamische Produktionsfunktion f t, Θ lassen sich analog zu Shephard/Färe (Shephard, R. W./Färe, R. 1980) formulieren. der effizienten Produktionsvektorfolgen bzw. die dynamische Produktionsfunktion f t, Θ lassen sich analog zu Shephard/Färe (Shephard, R. W./Färe, R. 1980) formulieren.
Für die hier vorgetragene Modifikation dynamischer Technologien gilt offensichtlich, dass man daraus
| 1. | für Θ → +∞ – abgesehen von der diskreten Zeitbetrachtung – das Konzept der dynamischen Produktionskorrespondenzen von Shephard/Färe (Shephard, R. W./Färe, R. 1980) erhält; | | 2. | für Θ = 1 die Beschreibung der dynamischen Aktivitätsanalyse durch Malinvaud (Malinvaud, E. 1953) herleiten kann; | | 3. | für Θ = 0 eine Auflösung dynamischer Produktionen in komparativ-statische Einzelfälle vornimmt; | | 4. | für Θ beliebig eine formal einheitliche Grundlage der zuvor behandelten, aus der Literatur bekannten Dynamisierungsformen bilden. kann. |
Literatur:
Baur, W. : Neue Wege der betrieblichen Planung, Berlin et al. 1967
Fandel, G. : Bedeutung der ökonomischen Theorie für das betriebswirtschaftliche Gebiet der Produktion, in: Betriebswirtschaftslehre und ökonomische Theorie, hrsg. v. Ordelheide, D./Rudolph, B./Büsselmann, E., Stuttgart 1990, S. 227 – 254
Fandel, G. : Produktion I, Produktions- und Kostentheorie, 6. A., Berlin et al. 2005
Fandel, G./Dyckhoff, H./Reese, J. : Industrielle Produktionsentwicklung, 2. A., Berlin et al. 1994
Fandel, G./Reese, J. : Kostenminimale Kraftwerksteuerung in einem Industriebetrieb, in: ZfB, 1988, S. 137 – 152
Färe, R. : Fundamentals of Production Theory, Berlin et al. 1988
Förstner, K./Henn, R. : Dynamische Produktions-Theorie und lineare Programmierung, Meisenheim/Glan 1957
Ihde, G. B. : Lernprozesse in der betriebswirtschaftlichen Produktionstheorie, in: ZfB, 1970, S. 451 – 468
Kistner, K.-P./Luhmer, A. : Ein dynamisches Modell des Betriebsmitteleinsatzes, in: ZfB, 1988, S. 63 – 83
Küpper, H.-U. : Dynamische Produktionsfunktion der Unternehmung auf der Basis des Input-Output-Ansatzes, in: ZfB, 1979, S. 93 – 106
Küpper, H.-U. : Interdependenzen zwischen Produktionstheorie und der Organisation des Produktionsprozesses, Berlin 1980
Leontief, W. : The Structure of the American Economy, 1919 – 1939, New York 1951
Lücke, W. : Produktions- und Kostentheorie, Würzburg et al. 1976
Malinvaud, E. : Capital Accumulation and Efficient Allocation of Resources, in: Ec, 1953, S. 233 – 268
May, E. : Dynamische Produktionstheorie auf der Basis der Aktivitätsanalyse, Heidelberg 1992
Shephard, R. W. : Dynamic Production Networks, in: Quantitative Studies on Production and Prices, hrsg. v. Eichhorn, W./Henn, R./Neumann, K. et al., Würzburg et al. 1983, S. 113 – 128
Shephard, R. W./Al-Ayat, R. A./Leachman, R. C. : Shipbuilding Production Function, in: Quantitative Wirtschaftslenkung, hrsg. v. Albach, H./Helmstädter, E./Henn, R., Tübingen 1977, S. 627 – 654
Shephard, R. W./Färe, R. : A Dynamic Theory of Production Correspondences, Operations Research Center Report 75 – 13, Univ. of California, Berkeley 1975
Shephard, R. W./Färe, R. : Dynamic Theory of Production Correspondences, Cambridge/Mass. 1980
Stöppler, S. : Dynamische Produktionstheorie, Opladen 1975
Trossmann, E. : Betriebliche Bedarfsplanung auf der Grundlage einer dynamischen Produktionstheorie, in: ZfB, 1986, S. 827 – 847
Wittmann, W. : Aktivitätsanalytische Ansätze dynamischer Produktionstheorie und ihre Beziehungen zur Planung, in: Unternehmenstheorie und Unternehmensplanung, hrsg. v. Mellwig, W., Wiesbaden 1979, S. 273 – 304
|