|
Erfahrungskurve
Inhaltsübersicht
I. Lerneffekte in der industriellen Fertigung und die Erfahrungskurve
II. Die Erfahrungskurve als Modell für Lern- und Erfahrungseffekte
III. Empirische Ergebnisse und Anwendungen der Erfahrungskurve
I. Lerneffekte in der industriellen Fertigung und die Erfahrungskurve
1. Lern- und Erfahrungskurve
Die wiederholte Durchführung eines beherrschbaren (Herstellungs-) Prozesses birgt die Chance, den für seine Anwendung notwendigen Ressourcenverbrauch aufgrund der gewonnenen Erfahrungen zu senken. Insbesondere wird man bei prozessbedingten manuellen Tätigkeiten erwarten, dass sich Übungsgewinne einstellen (learning by doing, Argote, L./Epple, D. 1990). Die wohl erste empirische Bestätigung für diese Aussage im Rahmen der industriellen Fertigung findet sich bei Wright (Wright, T.P. 1936). Er kann für den Flugzeugbau empirisch zeigen, dass die durchschnittlichen direkten Arbeitskosten pro Flugzeug (Lohnstückkosten) gemäß einer Potenzfunktion in der Anzahl hergestellter Maschinen fallen (vgl. auch den Zusammenhang zwischen Herstellungsdauern und Produktionsmenge im Flugzeugbau bei Rohrbach, A. 1927, S. 65). Eine solche Beziehung zwischen dem z.B. als Bearbeitungsdauer oder als Kostengröße gemessenen Arbeitsaufwand und einem Maß für die Lernerfahrung (z.B. Länge des Produktionszyklus, Anzahl Wiederholungen einer Tätigkeit) wird in der deutschsprachigen Literatur Lernkurve genannt (Mochty, L. 1996).
Wright stellt über den auf Übungsgewinnen beruhenden Lerneffekt hinaus fest, dass eine wachsende Fertigungserfahrung auf die durchschnittlichen gesamten Stückkosten eine analoge Wirkung hat. Die Erfahrungskurve gibt in ihrer einfachsten Fassung den Zusammenhang zwischen einem Maß für die Erfahrung, z.B. der kumulierten Fertigungsmenge eines Produktes, und einer geeignet gewählten, über die Lohnstückkosten hinausgehenden Kostengröße wieder. In der englischsprachigen Literatur werden die Begriffe experience curve und learning curve sowie u.a. progress curve allerdings oft synonym verwendet (anders Dutton, J.M./Thomas, A. 1984; Horngren, C.T./Foster, G./Datar, S.M. 2000, S. 344). Für die Erfahrungskurve wird als Verlaufsform i. Allg. ebenfalls eine Potenzfunktion angenommen.
2. Ursachen des Erfahrungskurveneffekts
Als Ursachen für den fallenden Verlauf der Stückkosten identifiziert bereits Wright neben den Übungsgewinnen u.a. konstruktionsbedingte Änderungen des Herstellungsverfahrens (Verwendung anderer Materialien und Teile, zunehmende Automatisierung, Substitution komplexer, einen hohen Ausbildungsstand voraussetzender Tätigkeiten durch einfache Arbeitsvorgänge usw.), die Standardisierung des Produkts, die Rüstkostendegression sowie Lernkurveneffekte bei den Zulieferern, die bezugspreissenkend wirken. Neben das unmittelbare learning by doing der am Fertigungsvorgang beteiligten Arbeitskräfte treten also durch die gewonnene Herstellungserfahrung des Unternehmens angestoßene Adaptionen z.B. im technischen oder planerischen Bereich, die Hirschmann als mittelbares Lernen der Organisation interpretiert (Hirschmann, W.B 1964). Die Literatur systematisiert die Ursachen für den Erfahrungskurveneffekt, also die mit zunehmender Fertigungserfahrung fallenden Stückkosten, gerne wie folgt (Lange, B. 1984; Wacker, P.-A. 1980, S. 58 ff.):
| - | Lernkurveneffekt: Aufgrund von Lernprozessen der objektbezogenen und der dispositiven Arbeit (Lernen der Organisation) sinken die Lohnstückkosten bei steigendem kumuliertem Produktionsvolumen. | | - | Technischer Fortschritt: Innovationen in der Verfahrenstechnik mit tendenziell kapitalintensiverer Fertigungsweise und Produktinnovationen, die einen höheren Standardisierungsgrad nach sich ziehen, führen i. Allg. zu niedrigeren variablen Kosten pro Stück. | | - | Rationalisierung: Die bislang genannten Ursachen führen i.d.R. nicht automatisch zu einem kostensenkenden Erfahrungskurveneffekt. Zur Wirkung gelangen sie erst durch gezielte betriebliche Maßnahmen, zu denen speziell auch FuE-Aktivitäten im Produkt- und Verfahrensbereich zu zählen sind (Prozess- und Produktinnovationen; vgl. Alberts, W. 1989 und Sinclair, G./Klepper, S./Cohen, W. 2000). | | - | Größeneffekte: Wachsende kumulierte Herstellungsmengen können, z.B. über zunehmende Seriengrößen bei gleichbleibendem Rüstaufwand pro Serie oder eine höhere Auslastung gegebener Kapazitäten, zu einer Fixkostendegression führen. Lerneffekte bei den Zulieferern und bestellmengenabhängige Bezugspreisminderungen tragen zu günstigeren Einkaufsbedingungen bei. |
Einen Überblick über Arbeiten, welche die Bedeutung dieser ineinander greifenden Ursachen für den Erfahrungskurveneffekt empirisch untersuchen, geben Dutton/Thomas (Dutton, J.M./Thomas, A. 1984).
II. Die Erfahrungskurve als Modell für Lern- und Erfahrungseffekte
1. Grundmodell und Verlaufsvarianten
Lern- und Erfahrungskurven werden in der Literatur auf gleiche Weise modelliert. Beispielsweise findet Wright als Zusammenhang zwischen den (durchschnittlichen) Stückkosten k(×) und der kumulierten Ausbringung x bei Stückkosten in Höhe von k0 für die erste Produkteinheit (z.B. aus der Nullserie) die Erfahrungskurve
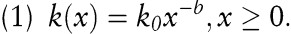
Die Parameter – b, die Elastizität der Stückkosten in Bezug auf die kumulierte Herstellungsmenge (Lange, B. 1984), und k0 sind dabei aus den jeweiligen Daten empirisch zu bestimmen. So ermittelt Wright aus seinen Flugzeugbau-Daten für b den Wert 0,322 und nennt die auf diese Weise spezifizierte Funktion k(×) eine 80 %-Kurve. Diese Bezeichnung resultiert daraus, dass sich durch eine Erhöhung der kumulierten Ausbringung auf ihr n-faches die Stückkosten auf das n-b-fache des Ausgangswertes reduzieren.
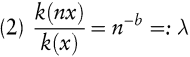
Die Stärke des Kostenrückgangs λ wird Lernrate genannt. Für Verdopplungen von beliebigen Mengen x ergibt sich gemäß der von Wright gefundenen Erfahrungskurve eine Senkung der Stückkosten um den Faktor λ = 2-0,322 = 0,8, also eine Lernrate von 80% (Verdopplungsgesetz, Wright, T.P. 1936, S. 124 f.).
Eine alternative Darstellung der Erfahrungskurve (1) ergibt sich, wenn man, beginnend mit der ersten hergestellten Produkteinheit, nur die jeweils verdoppelte Ausbringung betrachtet, sich also auf den Zusammenhang zwischen den Stückkosten und xm = 2m, m = 0, 1, 2,..., beschränkt. Für diese Ausbringungsmengen lässt sich (1) wegen λ = 2-b in
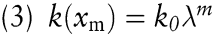
umformen. Beobachtet man in zwei verschiedenen Zeitpunkten die kumulierten Herstellungsmengen xm und xn, 0 < xm < xn , gilt
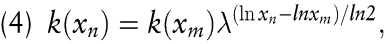
wobei der Exponent die Anzahl notwendiger Verdopplungen von xm angibt, um schließlich die Ausbringung xn zu erhalten. (4) ist auch für Ausbringungsmengen richtig, die keine ganzzahligen Potenzen von zwei sind. In diesem Fall ist der Exponent der Lernrate u.U. keine natürliche Zahl.
Im Zuge der empirischen Auseinandersetzung mit Lernkurven wurde eine Reihe von Varianten zu der in der logarithmischen Darstellung linearen Verlaufsform (1) vorgeschlagen (Yelle, L.E. 1979; Wacker, P.-A. 1980, S. 22 ff.). Die Wrightsche Erfahrungskurve ist durch eine konstante Lernrate gekennzeichnet. U. U. wird es bei der Einführung eines neuen Produktionsprozesses jedoch möglich sein, Lerneffekte von ähnlichen Fertigungsverfahren oder Produkten zu übertragen. Die Standford-B-Kurve berücksichtigt diesen Aspekt durch eine in der Anfangsphase abgesenkte Kostenreduktion (logarithmisch-konkaver Verlauf). Mit zunehmender Fertigungserfahrung sinkende Lernraten modelliert die logarithmisch-konvexe Lernkurve. Weitere Verlaufsformen sind u.a. das Plateau-Modell (die Lernrate ist ab einer bestimmten Fertigungserfahrung gleich null) und die logarithmisch-S-förmige Kurve mit einem zunächst konkaven, dann linearen und schließlich konvexen Verlauf (Kombination der beschriebenen Effekte).
2. Durchschnittskurve, Einheitskurve und Kostendefinition
Die Erfahrungskurve (1) wird in der Literatur in Form der Durchschnitts- oder der Einheitskurve verwendet (Schneider, D. 1965; Horngren, C.T./Foster, G./Datar, S.M. 2000, S. 344). Bei gleicher Definition des Maßes für die Fertigungserfahrung (z.B. die kumulierte Ausbringung) ist bei der Durchschnittskurve (kD(×)) die abhängige Größe wie oben als durchschnittliche Stückkosten zu interpretieren, während sie bei der Einheitskurve (kE(×)) den Stückkosten der letzten Produkteinheit entspricht (Marginalkosten). In welcher Form (1) die Erfahrungseffekte besser beschreibt, hängt von der jeweiligen betrieblichen Situation ab und kann daher nicht allgemein entschieden werden. Bei der Anwendung oder dem Vergleich von empirischen Studien sind aber die Unterschiede zwischen den beiden Konzepten zu beachten. So sind die Gesamtkosten für x nach der Durchschnittskurve gleich dem Produkt xkD(x), für die Einheitskurve ergeben sie sich aus der Kumulation über die einzelnen Ausbringungsniveaus. Misst man die Ausbringung etwa als kontinuierliche Größe, lauten die Gesamtkosten in diesem Fall
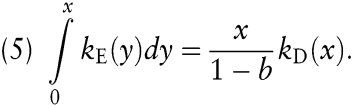
Entsprechend sind die durchschnittlichen Stückkosten nach der Einheitskurve gleich kD(x)/(1-b). Die Interpretation von (1) als Durchschnittskurve unterstellt damit bei gleichen Parameterwerten eine stärkere Reduktion der Stückkosten der jeweils letzten hergestellten Einheit als die Einheitskurve (vgl. das Beispiel bei Horngren, C.T./Foster, G./Datar, S.M. 2000, S. 345 f.).
Wright benutzt unterschiedliche inhaltliche Fassungen der Kostengröße in (1) (Wright, T.P. 1936). Um den Lernkurveneffekt zu zeigen, interpretiert er k(×.) als durchschnittliche Lohnstückkosten (kD(×.)). Kostenartspezifische Erfahrungskurven leitet er ferner für die Materialkosten (inkl. Abfall und Ausschuss) sowie für den (manufacturing) overhead (inkl. Material- und Fertigungsgemeinkosten) her. Wright verwendet seine Beobachtungen aber auch, um mit Hilfe eines Vergleichs mit den Erfahrungskurveneffekten im Automobilbau die Preisentwicklung und die Marktchancen von Flugzeugen zu prognostizieren. In diesem Zusammenhang nutzt er eine Erfahrungskurve für die Summe dieser Kostenarten. Damit deutet sich schon ein guter Teil des Rahmens an, innerhalb dessen die nachfolgende Literatur nach geeigneten Definitionen der Kostengröße in (1) sucht. Die wachsende Fertigungserfahrung etwa wirkt i. Allg. mit unterschiedlicher Intensität auf die verschiedenen Kostenarten ein, die kostenartspezifischen Erfahrungskurven weisen daher i.d.R. eine unterschiedliche Lernrate auf (Wright, T.P. 1936; Day, G.S./Montgomery, D.B. 1983; Lange, B. 1984). Umfasst k(×.) die Summe einzelner Kostenarten, ist wegen des langen Betrachtungszeitraumes die Berücksichtigung von Gemeinkostenanteilen und kurzfristig fixen Kosten üblich. Allerdings verschärft sich im Zusammenhang mit Erfahrungskurveneffekten die Zurechnungsproblematik solcher Kosten, wenn sich Zuschlagsbasen und Verrechnungsgrößen wegen der kostenartspezifischen Kostenreduktionen verändern (Day, G.S./Montgomery, D.B. 1983; Lange, B. 1984).
Marktbedingte Faktorpreisvariationen können einen erfahrungsbedingten Rückgang der Stückkosten verzerren. Day und Montgomery schlagen daher vor, die Kosten extern bezogener Materialien nicht einzubeziehen, falls sie einen bedeutenden Anteil an allen betrachteten Kosten ausmachen und starken Preisschwankungen ausgesetzt sind (vgl. auch Henderson, D.B. 1974; Sinclair, G./Klepper, S./Cohen, W. 2000). Andererseits führen wachsende Ausbringungsmengen auch bei den Zulieferern zu Erfahrungskurveneffekten, die berücksichtigt werden sollten, wenn die Preisentwicklung eines Produktes im Rahmen der strategischen Unternehmensplanung analysiert wird. Ähnlich wie die erwähnten Preisschwankungen überlagert auch eine nachhaltige Geldentwertung u.U. den Erfahrungskurveneffekt; Überlegungen zur Deflationierung der betroffenen Daten finden sich z.B. bei Day/Montgomery und Lange (Day, G.S./Montgomery, D.B. 1983; Lange, B. 1984). Wird die Erfahrungskurve wiederum im Kostenmanagement eingesetzt, um gezielt Kostensenkungsmaßnahmen durchzuführen, sollten nur die vom Unternehmen kontrollierbaren Kosten in die Definition von k(·) Eingang finden (Day, G.S./Montgomery, D.B. 1983). Insgesamt zeigt sich, dass die adäquate Fassung des Kostenbegriffs von der intendierten Anwendung der Erfahrungskurve abhängig ist.
III. Empirische Ergebnisse und Anwendungen der Erfahrungskurve
1. Empirischer Befund
Wright nachfolgend ist eine große Zahl von empirischen Untersuchungen zum Erfahrungskurveneffekt veröffentlicht worden (Wright, T.S. 1936, vgl. die Übersichtsartikel Yelle, L.S. 1979; Dutton, J.M./Thomas, A. 1984 sowie Argote, L./Epple, D. 1990). Ein großer Teil dieser Arbeiten beschäftigt sich damit, die Parameter von Erfahrungskurven vom Typ (1) zu schätzen. So untersucht Alchian schon relativ früh mittels regressionsanalytischer Methoden typen- und fertigungsstättenspezifische Einheitskurven für verschiedene Flugzeugtypen unterschiedlicher Hersteller. (Alchian, A. 1963). Erfahrungskurven wurden daneben im Schiffbau, im Automobilbau, für die Papierherstellung, die Herstellung elektronischer Bauteile, die chemische Industrie, im Dienstleistungsbereich usw. gefunden. Allerdings zeigt Alchian auch, dass die typen- und fertigungsstättenspezifischen Lernraten sich deutlich voneinander unterscheiden. Ferner führt nach seinen Ergebnissen die Verwendung einer Industrielernkurve, die alle verfügbaren Daten für die verschiedenen Produkttypen und Fabriken repräsentiert, gegenüber den spezifischen Lernkurven zu erheblichen Verzerrungen der Kostenprognosen. Alchians Befund ist in der Erfahrungskurvenliteratur vielfach bestätigt worden. Lernraten variieren mit der Branche, mit dem Unternehmen, innerhalb eines Unternehmens für ein Produkt mit der Fertigungsstätte und dem Fertigungsverfahren usw. (Yelle, L.E. 1979; Sinclair, G./Klepper, S./Cohen, W. 2000). Eine Auswertung von mehr als 100 empirischen Studien durch Dutton/Thomas zeigt eine Streuung der gefundenen Lernraten im Wesentlichen in einem Intervall von 55% bis 96% mit einem Modalwert bei einer Lernrate von 80% (Dutton, J.M./Thomas, A. 1984). Insbesondere der Umstand, dass innerhalb eines Unternehmens bei dem gleichen Produkt in unterschiedlichen Fertigungsstätten variierende Lernraten auftreten (z.B. Argote, L.D./Epple, D. 1990) legt die Vermutung nahe, dass die monokausale Erklärung der Kostenreduktion durch die kumulierte Ausbringung oder ein gleichwertiges Maß für die Fertigungserfahrung in (1) zu kurz greift.
In der empirisch orientierten Literatur ist daher eine Tendenz festzustellen, die kumulierte Ausbringung durch andere Erklärungsgrößen zu ergänzen. Bezüglich der Lernkurveneffekte sind der Automatisierungsgrad sowie der Planungsaufwand vor Beginn der Fertigung (Yelle, L.E. 1979), das Vergessen von Erfahrungen durch das Unternehmen (organizational forgetting), der Personalwechsel und der Wissenstransfer zu nennen (Argote, L./Epple, D. 1990; Argote, L./Beckmann, S.L./Epple, D. 1990; Darr, E.D./Argote, L./Epple, D. 1995). Eine besondere Rolle spielen in diesem Zusammenhang Einflussgrößen, die als betriebliche Umsetzung des technischen Fortschritts zu interpretieren sind. So stellt Liebermann (Lieberman, M.B. 1984) in seiner regressionsanalytischen Studie für die chemische Industrie fest, dass neben dem kumulierten Output das Volumen der Neuinvestitionen (vgl. auch Sheshinski, E. 1967) und die FuE-Aufwendungen einen wichtigen Beitrag zur Erklärung des Erfahrungskurveneffekts liefern. Adler/Clark weisen u.a. die Bedeutung konstruktiver Veränderungen der Produkte nach (Adler, P.S./Clark, K.B. 1991). In eine ähnliche Richtung deutet die sehr gründliche Arbeit von Sinclair et al. (Sinclair, G./Klepper, S./Cohen, W. 2000). Für ein Unternehmen der kapitalintensiven chemischen Industrie gelingt es ihnen zu zeigen, dass die ermittelten Erfahrungskurveneffekte auf die Durchführung von FuE-Projekten zurückzuführen waren. Die Projekte änderten die Fertigungsverfahren, griffen dabei aber nicht auf Fertigungserfahrungen zurück. Der Anreiz für die Unternehmensführung, bestimmte Produkte für die FuE-Projekte auszuwählen, war die kumulierte Ausbringung, die dem Management als Indikator für das künftige Absatzvolumen diente. Die in den Erfahrungskurven erfasste Korrelation zwischen den Stückkosten und der kumulierten Ausbringung war also nur scheinbar kausal auf den Zuwachs an Fertigungserfahrung zurückzuführen.
2. Anwendungsgebiete der Erfahrungskurve
Lernkurveneffekte beeinflussten zunächst die Prognose von Kosten und Fertigungszeiten für die Kriegsproduktion von Flugzeugen und Schiffen durch die U.S.-Regierung. Verwandte Anwendungen finden sich in Kostenrechnung und -management. Zu nennen sind die Berücksichtigung der Erfahrungskurve in der Kostenplanung, der Abweichungsanalyse, der Break-Even-Analyse (Yelle, L.E. 1979; Coenenberg, A.G. 1999, S. 209 f.) oder im Target Costing (Betz, S. 1995). Stark popularisiert wurde das Konzept in den 70er-Jahren des letzten Jahrhunderts durch die Boston Consulting Group (Henderson, B.D. 1974; Yelle, L.E. 1979), die aus Industriepreiskurven (die Rolle der abhängigen Variablen in (1) übernimmt der durchschnittliche Preis in einer Branche) Empfehlungen für die strategische Unternehmenspolitik ableitete. Insbesondere ist das Streben nach einem dominanten Marktanteil zu nennen, der wegen der im Vergleich zu den Konkurrenten großen Ausbringungsmenge durch den Erfahrungskurveneffekt zu niedrigen Stückkosten und hoher Profitabilität führt (Hedley, B. 1976, Portfoliomodelle). Vor dem Hintergrund des oben referierten empirischen Befunds ist die Aussagekraft von Industiepreiskurven allerdings kritisch einzuschätzen. Ferner erscheint die Kausalität zwischen dem Wachsen der Ausbringung und dem Sinken der Stückkosten, die z.B. der zitierten Strategieempfehlung zugrunde liegt, fragwürdig (Alberts, W.W. 1989). Verstärkt werden diese Zweifel durch die empirisch nachweisbare Bedeutung des spillover-Lernens von konkurrierenden Unternehmen (Jarmin, R.S. 1994). Allgemein wäre ein Einsatz von Erfahrungskurven eines Unternehmens in der strategischen Planung insbesondere vor dem Beginn der Fertigung des betrachteten Produkts nützlich. Der empirische Befund zeigt aber den produkt- und fertigungsstättenspezifischen Charakter der Erfahrungskurve, sodass die Schätzung ihrer Parameter nur aus der schon angelaufenen Fertigung stammen kann (Schneider, D. 1965; Zangwill, W.J./Kantor, P.B. 2000).
Literatur:
Adler, Paul S./Clark, Kim B. : Behind the Learning Curve: A Sketch of the Learning Process, in: Management Science, Jg. 37, 1991, S. 267 – 281
Alberts, William W. : The Experience Curve Doctrine Reconsidered, in: Journal of Marketing, Jg. 53, 1989, S. 36 – 49
Alchian, Armen : Reliability of Progress Curves in Airframe Production, in: Econometrica, Jg. 31, 1963, S. 679 – 693
Argote, Linda/Epple, Dennis : Learnig Curves in Manufacturing, in: Science, Jg. 247, 1990, S. 920 – 924
Argote, Linda/Beckman, Sara L./Epple, Dennis : The Persistence and Transfer of Learning in Industrial Settings, in: Management Science, Jg. 36, 1990, S. 140 – 154
Betz, Stefan : Die Erfahrungskurve als Instrument der Zielkostenspaltung, in: BFuP, Jg. 47, 1995, S. 609 – 625
Coenenberg, Adolf G. : Kostenrechnung und Kostenanalyse, Landsberg am Lech, 4. A., 1999
Darr, Eric D./Argote, Linda/Epple, Dennis : The Acquisition, Transfer, and Depreciation of Knowledge in Service Organizations: Productivity in Franchises, in: Management Science, Jg. 41, 1995, S. 1750 – 1762
Day, George S./Montgomery, David B. : Diagnosing the Experience Curve, in: Journal of Marketing, Jg. 47, 1983, S. 44 – 58
Dutton, John M./Thomas, Annie : Treating Progress Functions as a Managerial Opportunity, in: Academy of Management Review, Jg. 9, 1984, S. 235 – 247
Hedley, Barry : A Fundamental Approach to Strategy Development, in: Long Range Planning, Jg. 9, 1976, S. 2 – 11
Henderson, Bruce D. : Die Erfahrungskurve in der Unternehmensstrategie, Frankfurt a. M. 1974
Hirschmann, Winfred B. : Profit From the Learnig Curve, in: Harvard Business Review, 1964, Jg. 42, S. 125 – 139
Horngren, Charles T./Foster, George/Datar, Srikant M. : Cost Accounting, London, 10. A., 2000
Jarmin, Ronald S. : Learning by doing and competition in the early rayon industry, in: Rand Journal of Economics, Jg. 25, 1994, S. 441 – 454.
Lange, Bernd : Die Erfahrungskurve: Eine kritische Beurteilung, in: ZfbF, Jg. 36, 1984, S. 229 – 245
Lieberman, Marvin B. : The learning curve and pricing in the chemical processing industries, in: Rand Journal of Economics, Jg. 15, 1984, S. 213 – 228
Mochty, Ludwig : Lernen in der industriellen Produktion, in: HWProd, hrsg. v. Kern, Werner/Schröder, Hans-Horst/Weber, Jürgen, Stuttgart, 2. A., 1996, Sp. 1074 – 1085
Rohrbach, Adolph : Economic Production of All-Metal Airplanes and Seaplanes, in: The Journal of the Society of Automotive Engineers, H. 1/1927, Bd. XX, S. 57 – 66
Schneider, Dieter : „ Lernkurven “ und ihre Bedeutung für Produktionsplanung und Kostentheorie, in: ZfbF, Jg. 17, 1965, S. 501 – 515
Sheshinski, Eytan : Test of the „ Learning by Doing “ Hypothesis, in: Review of Economics and Statistics, Jg. 49, 1967, S. 568 – 578
Sinclair, Gavin/Klepper, Steven/Cohen, Wesley : What\'s Experience Got to Do With It ? Sources of Cost Reduction in a Large Specialty Chemicals Producer, in: Management Science, Jg. 46, 2000, S. 28 – 45
Wacker, Peter-Alexander : Die Erfahrungskurve in der Unternehmensplanung, München 1980
Wright, T.P. : Factors Affecting the Cost of Airplanes, in: Journal of the Aeronautical Sciences, 1936, Bd. 3, S. 122 – 128
Yelle, Louis E. : The Learning Curve: Historical Review and Comprehensive Survey, in: Decision Science, Jg. 10, 1979, S. 302 – 328
Zangwill, Willard I./Kantor, Paul B. : The learning curve: a new perspective, in: International Transactions in Operations Research, 2000, S. 595 – 607
|