Grenzproduktivitätstheorie

Die G. stellt ein zentrales Element der Neoklassischen Theorie dar, die sowohl die Frage einer effizienten Allokation der Ressourcen als auch die Frage nach den Bestimmungsgründen der Faktornachfrage und -entlohnung (Faktorpreisbildung) und somit nach der funktionalen Verteilung des Volkseinkommens (funktionelle Einkommensverteilung) zu beantworten versucht. Es kann gezeigt werden, daß die Ressourcen unter Annahme rationaler Optimierungskalküle der Wirtschaftssubjekte durch den Lenkungsmechanismus des Preissystems (Preisfunktion) ihrer produktivsten Verwendung zugeführt werden (Allokationsfrage), da die Produktionsfaktoren nach dem Beitrag entlohnt werden, den sie zur Erstellung eines Gutes leisten (Distributionsfrage). Dies setzt allerdings voraus, daß die Faktoren mobil sind und somit die notwendigen Anpassungsbewegungen bei Änderungen der Präferenzstrukturen , der Technologie oder anderer exogener Schocks (Politik, Wetter, etc.) vollziehen können. Nimmt man an, daß für ein einzelnes Unternehmen (Betrieb, I.) die Produktionstechnologie gegeben sei (Produktionsfunktion: O = O (v1, v2, ..., vn), vi = Inputfaktoren), ebenso wie die Faktorentlohnung je Faktoreinheit (li) und daß ferner Güter - und Faktormärkte entweder vollkommen oder monopolistisch organisiert sind (Marktformen), so stellt sich die Frage nach der mengenmäßigen Faktornachfrage des Unternehmens. Die Gewinnfunktion (Gewinntheorie) lautet bei Konstanz aller Faktoren vi außer v1:               


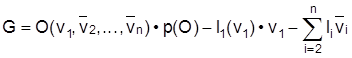
, p = Güterpreis, und die Bedingung
1. und
2. Ordnung für ein Gewinnmaximum (Gewinnmaximierung) hinsichtlich v1 beträgt:            


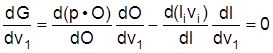
od. unter Verwendung der Preiselastizität der Güternachfrage h (Elastizitäten) und der Faktorentlohnungselastizität des Faktorangebots e1                     


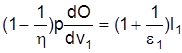
wobei der Ausdruck p · dO/dv1 die bewertete Grenzproduktivität des Faktors v1 repräsentiert. Dieses Ergebnis gilt analog auch für alle anderen Faktoren i, i ¹
1. Herrscht sowohl auf den Güter- als auch auf den Faktormärkten vollständige Konkurrenz, so betragen die Elastizitäten h = e1 = e2 = ... = en = ¥ und die Optimalbedingung reduziert sich zu               


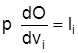
, für alle Faktoren i. Damit ist das Grenzwertprodukt gleich der nominellen Faktorentlohnung bzw. das physische Grenzprodukt gleich der realen Faktorentlohnung         


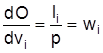
für alle Faktoren i. Die Höhe der Faktorentlohnung und der Umfang der Faktornachfrage hängt folglich von den Grenzproduktivitäten ab, die sich wiederum aus der angewandten Produktionstechnologie ergeben. Ein Unternehmen fragt so lange zusätzliche Produktionsfaktoren nach, bis der produktive Beitrag der zuletzt eingesetzten Faktoreinheit gerade seiner Entlohnung entspricht. Anders gesagt: Bei einer gegebenen Faktornachfrage werden alle Faktoren nach der Produktivität der zuletzt eingesetzten Faktoreinheit entlohnt. In der G. werden häufig linear homogene Produktionsfunktionen (Produktionsfunktion) verwendet, da sie nach dem Eulerschen Theorem die Eigenschaft besitzen, daß der Outputwert vollständig auf die Produktionsfaktoren aufgeteilt wird und somit eine geeignete Theorie der funktionellen Einkommensverteilung vorzuliegen scheint. Darüber hinaus konnten C. W. Cobb und P. Douglas die These einer linear homogenen Produktionsfunktion für die gesamte Volkswirtschaft (Wirtschaft) der USA empirisch nachweisen. In der Folgezeit sind sowohl an den empirischen Ergebnissen als auch an der logischen Konsistenz der G. Kritik geübt worden, auf die noch einzugehen sein wird. Für eine homogene Produktionsfunktion vom r-ten Grade mit einem beliebigen Vervielfachungsfaktor l > 0                                    


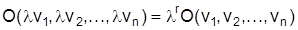
(Homogenitätskriterium) gilt bei partieller Ableitung nach l            


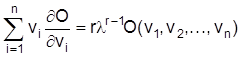
Im Falle einer linear homogenen Produktionsfunktion r = 1 reduziert sich der Ausdruck auf der rechten Seite zu O. Multipliziert man beide Seiten mit dem Produktpreis (bzw. Preisniveau in makroökonomischen Betrachtungen), so zeigt sich, daß langfristig die Kosten der Produktion gleich dem Produktionswert sind.            


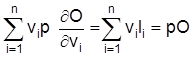
Damit wird der Produktionswert vollständig auf die eingesetzten Faktoren aufgeteilt, was mit anderen Worten bedeutet, daß der langfristige Gewinn Null beträgt. Dieses Ergebnis kann auch durch eine Cobb-Douglas-Funktion            


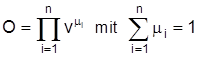
veranschaulicht werden. Die Grenzproduktivität des ersten Faktors lautet            


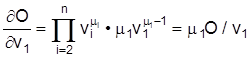
Führt man die Berechnung für alle Produktionsfaktoren durch, multipliziert die Grenzproduktivität mit den Faktoreinsatzmengen und dem Produktpreis (bzw. dem Preisniveau) und summiert über alle Faktorkosten, so erhält man            


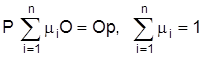
Es zeigt sich, daß die partiellen Produktionselastizitäten mi der Cobb-Douglas-Funktion den Anteil der Faktorentlohnung am Outputwert (bzw. Volkseinkommen) bestimmen. Ihre Summe gibt den Homogenitätsgrad der Produktionsfunktion an und repräsentiert gleichzeitig die Skalenelastizität der Produktion k. Ist der Homogenitätsgrad größer als 1, so übersteigt die Faktorentlohnung den Outputwert, ist er kleiner als 1, so verbleibt vom Outputwert ein unverteilter Rest (Gewinn), da die gesamte Faktorentlohnung geringer ist. Nimmt man entsprechend der G. jedoch linear homogene Produktionsfunktionen, so ist der Gewinn unabhängig vom Produktpreis gleich Null. Die Ursache für dieses bemerkenswerte Ergebnis ist in der Tatsache zu sehen, daß die Gewinnfunktion gleichfalls homogen vom Grade eins ist:            


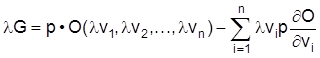
Die Kombination der Produktionsfaktoren v1, v2, ..., vn ist derart, daß genau ein Nullgewinn entsteht. Die Vervielfältigung der Inputfaktoren mit l führt daher für jedes beliebige l wiederum zu einem Nullgewinn. Würden die Faktorkombinationen v1, v2, ..., vn einen Gewinn bzw. Verlust hervorbringen, so würde dieser Zustand aufgrund der linear homogenen Gewinnfunktion für alle beliebigen Ausbringungsmengen erhalten bleiben. Die Annahme einer linear homogenen Produktionsfunktion hat darüber hinaus die Eigenschaft, daß die Grenzen der Outputausdehnung der Unternehmen endogen nicht erklärt werden können. Unterstellt man hingegen eine beliebige nichthomogene Produktionsfunktion und die Existenz der Gewinnmaximierungsbedingungen erster und zweiter Ordnung sowie einen aufgrund von Marktein- und Marktaustritten langfristig entstandenen Nullgewinn für die Unternehmen, so kann die vollständige Aufteilung des Outputwertes ebenfalls gezeigt werden:            


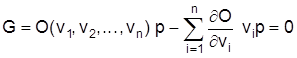
od.            


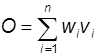
Dabei ist es allerdings notwendig, exogene Erklärungen für das Zustandekommen des langfristigen, gewinnlosen Gleichgewichts heranzuziehen. Alle weiteren Kritikpunkte zur G. betreffen den empirischen Gehalt der Annahmen, so etwa die Vorstellung der vollkommenen Konkurrenz auf den Güter- und Faktormärkten. Wird diese Annahme aufgegeben und endliche Preiselastizitäten der Güternachfrage und Faktorentlohnungselastizitäten der Faktornachfrage zugelassen, so entstehen positive Gewinne, deren Existenz ebenso wie die sich ergebende Verteilung aus dem Monopolisierungsgrad der Märkte erklärt werden müßten. Damit wird aber der rein "technologische" Ansatz der G. verlassen.

Literatur: J. M. Henderson/R. E. Quandt, Mikroökonomische Theorie.
5. A., München 1983, 107-112. A. E. Ott, Grundzüge der Preistheorie.
3. A., Göttingen 1984, 273-293.