|
Produktionstheorie, aktivitätsanalytische
Inhaltsübersicht
I. Problemstellung
II. Grundlagen der Aktivitätsanalyse
III. Ergebnisse der linearen Aktivitätsanalyse
IV. Erweiterte Technologien ohne Verschwendung
I. Problemstellung
Gegenstand der Produktionstheorie sind die Beziehungen zwischen Faktoreinsatz- und Ausbringungsmengen, die formal in Produktionsfunktionen bzw. in Produktionskorrespondenzen erfasst werden. Während die neoklassische funktionalistische Produktionstheorie die Existenz einer zweimal stetig differenzierbaren Produktionsfunktion mit konstanten oder abnehmenden Skalenerträgen, abnehmender Grenzrate der Substitution und abnehmenden Ertragszuwächsen postuliert, geht die Aktivitätsanalyse von formalen Eigenschaften der Technologie, d.h. der Menge der technisch realisierbaren Produktionen, aus. Sie leitete daraus Eigenschaften der Produktionsfunktion und Empfehlungen für Produktionsentscheidungen, d.h. für die Wahl zwischen alternativen Kombinationen von Faktoreinsatz- und Ausbringungsmengen, her.
Die Aktivitätsanalyse wurde von Koopmans (Koopmans, T. C. 1951) konzipiert und von Debreu (Debreu, G. 1959) in die mikroökonomische Gleichgewichtstheorie integriert. Im deutschen Sprachbereich wurde die Aktivitätsanalyse insb. durch die Arbeiten von Beckmann (Beckmann, M. J. 1955, Beckmann, M. J. 1960) und Wittmann (Wittmann, W. 1966; Wittmann, W. 1968) bekannt. Neuere Ansätze zur Formulierung der bwl. Produktionstheorie auf der Grundlage der Aktivitätsanalyse finden sich u.a. bei Kistner (Kistner, K.-P. 1981a; Kistner, K.-P. 1981b; Kistner, K.-P. 1993a), Fandel (Fandel, G. 1991), Dyckhoff (Dyckhoff, H. 1993a; Dyckhoff, H. 1993b; Dyckhoff, H. 1994).
Im Folgenden werden zunächst die Grundlagen der Aktivitätsanalyse und die Postulate der Theorie linearer Technologien dargestellt. Im Anschluss daran werden die wichtigsten Ergebnisse der linearen Aktivitätsanalyse, insb. die Eigenschaften der Produktionsfunktion bei linearen Technologien, untersucht. Neben den traditionellen Ansätzen, die die Verschwendung von Gütermengen zulassen, werden erweiterte Technologien untersucht, bei denen unerwünschte Güter nur durch Einsatz von Faktoren vernichtet werden können.
II. Grundlagen der Aktivitätsanalyse
1. Allgemeines
Ausgangspunkt der Aktivitätsanalyse ist der Begriff der Aktivität, eine Kombination von Einsatzmengen (r = (r1, ?,rn) der Faktoren i = (1, ?,n), die eine bestimmte Kombination von Ausbringungsmengen x = (x1, ?,xm) der Produkte j = (1, ?,m) ermöglicht. Eine Aktivität kann als ein Punkt y = (r, x) des ℜn+m dargestellt werden; man spricht daher auch von Produktionspunkten. Eine solche Beschreibung der Produktion setzt voraus, dass die in der Produktion eingesetzten Produktionsfaktoren und die erzeugten Produkte messbar sind.
Die Menge der technisch möglichen Aktivitäten T: = {y | y ist technisch realisierbar}, über die eine Wirtschaftseinheit verfügt, bezeichnet man als Technologie-Menge. Die Aktivitätsanalyse postuliert, dass diese folgende Eigenschaften besitzt (vgl. Debreu, G. 1959, S. 40):
Axiome der Aktivitätsanalyse:

Unter effizienten Aktivitäten versteht man Produktionspunkte, bei denen keine Produktionsfaktoren verschwendet werden, sodass es nicht möglich ist, Einsatzmengen einzelner Faktoren zu reduzieren, ohne dass die Ausbringungsmengen der Produkte verringert oder die Einsatzmengen anderer Faktoren erhöht werden müssen. Sie genügen dem Effizienzkriterium:
Definition: Effizienzkriterium
Eine Aktivität yo = (ro,xo) ∊ T heißt effizient, falls es keine andere Aktivität y = (r,x) ∊ T gibt, sodass ro ≥ r; xo ≤ x und rio > ri für mindestens einen Faktor i oder xoj < xj für mindestens ein Produkt j.
2. Lineare Technologien
In der bwl. Produktionstheorie betrachtet man insb. lineare Technologien, die durch folgende Eigenschaften charakterisiert sind:
(1) Proportionalität: Falls eine Aktivität y = (r,x) ∊ T technisch möglich ist, dann ist auch jede Aktivität
λ · y = (λ · r1, ?,λ · rn,λ · x1, ?,λ · xm) ∊ T
für alle λ ≥ 0, d.h. technisch möglich.
Proportionalität impliziert die beliebige Teilbarkeit von Produktionsfaktoren und Ausbringungsmengen. Auch wenn diese Annahme auf den ersten Blick sehr restriktiv erscheint, gilt sie bei geeigneten Messvorschriften zumindest näherungsweise: So sind zwar Maschinen unteilbar, nicht jedoch deren Einsatzzeit; nicht ganzzahlige Ausbringungsmengen bedeuten, dass die letzte Einheit während der Planungsperiode nur teilweise fertiggestellt wird.
(2) Additivität: Mit jedem Paar von Aktivitäten y1 = (r1,x1) ∊ T und y2 = (r2,x2) ∊ T ist auch jede Aktivität
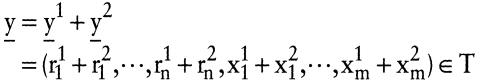
Additivität setzt voraus, dass keine Interaktionen zwischen Aktivitäten zu berücksichtigen sind; das ist nur dann möglich, wenn wirklich alle Faktoreinsatzmengen erhöht werden können. Interdependenzen, die sich aus beschränkten Faktorbeständen – wie z.B. Maschinenkapazitäten – ergeben, werden nicht als Einschränkung der Technologiemenge berücksichtigt; sie können vielmehr als zusätzliche Restriktionen erfasst werden, welche die Menge der technisch möglichen Alternativen einschränken.
(3) Möglichkeit der Verschwendung: Faktoreinsatz ohne Ausbringung ist möglich: y = (r,0) ∊ T für alle r ≥ 0. Eine solche Verschwendung von Faktoreinsatzmengen lässt sich vielfach als Stillstand von Maschinen bzw. als Lagerung von nicht genutzten Werkstoffbeständen interpretieren. Modifikationen dieser Annahme sind Gegenstand des vierten Abschnitts dieses Beitrags.
Wegen der Proportionalität gehören alle Aktivitäten y, die auf einem vom Koordinatenursprung ausgehenden Strahl durch einen Produktionspunkt y* = (r*,x*) ∊ T liegen, ebenfalls zur Technologiemenge. Diese Aktivitäten, die auf dem gleichen technischen Verfahren beruhen, gehören zu einem Produktionsprozess.
Definition: Produktionsprozess
Es sei y* = (r*,x*) ∊ T eine technisch mögliche Aktivität. Dann heißt die Menge π: = {y | y = λ · y*, λ ≥ 0) Produktionsprozess (zu y*).
In Abb. 1 sind drei Produktionsprozesse πo, π1, p2 für den Fall des Produkts zweier Produktionsfaktoren dargestellt. Auf den Koordinatenachsen sind die Einsatzmengen der beiden Faktoren abgetragen. Die mit einer bestimmten Kombination von Faktoreinsatzmengen erreichbare Ausbringungsmenge x¯ ist auf den Prozessstrahlen πk abgetragen.
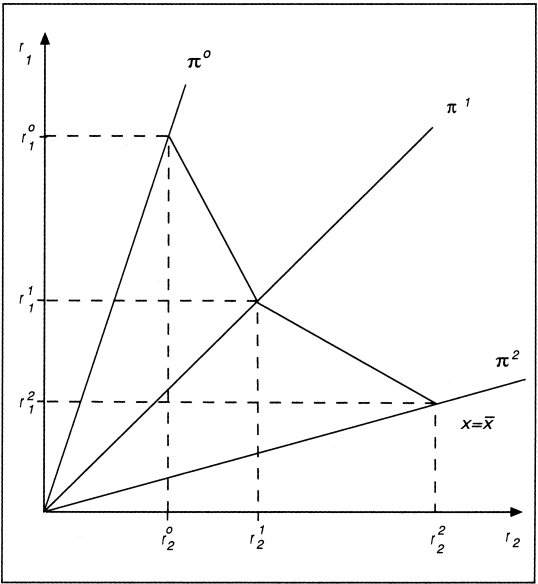
Abb. 1: Aktivitäten und Produktionsprozesse
Bei einem Produktionsprozess stehen die Einsatzmengen der Faktoren und die Ausbringungsmengen der Produkte in einem festen Verhältnis zueinander. Mit der Festlegung der Ausbringungsmenge xj > 0 eines Produkts sind sowohl die Einsatzmengen der Faktoren als auch die Ausbringungsmengen der anderen Produkte bestimmt. Man kann daher die Ausbringungsmenge eines Standardprodukts dazu verwenden, das Prozessniveau z zu messen. Die auf das Niveau z eines Prozesses π bezogenen Produktionskoeffizienten sind definiert als
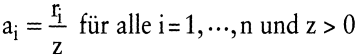
Ebenso erhält man für die Koppelungskoeffizienten
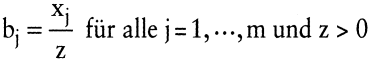
Ein Produktionsprozess ist dann eindeutig durch den (n+m)-dimensionalen Spaltenvektor a = (a1, ?,an,b1, ?,bm)T determiniert; man erhält jeden Punkt auf dem Prozessstrahl, indem man den Vektor a mit einem beliebigen Prozessniveau z ≥ 0 multipliziert.
Additivität und Proportionalität erlauben es, Konvexkombinationen von Aktivitäten zu bilden:
Falls y1 = (r1,x1), y2 = (r2,x2), ?, ys = (rs,xs) ∊ T,
dann ist für alle
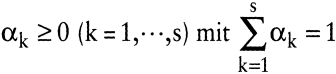
auch 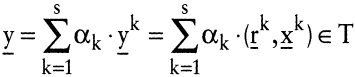 . .
Durch Variation der Gewichte αk kann jeder Produktionspunkt auf der durch die Punkte yk aufgespannten Fläche realisiert werden. Im Fall von zwei Produktionsfaktoren liegen alle Kombinationen von zwei Aktivitäten auf der Strecke zwischen beiden Produktionspunkten (vgl. Abb. 1).
Da auch die kombinierte Aktivität proportional variiert werden kann, definiert jede Konvexkombination von Aktivitäten einen gemischten Produktionsprozess.
Die Technologie-Menge einer linearen Technologie ist die Vereinigungsmenge aller reinen und gemischten Prozesse. Fasst man die Koeffizientenvektoren spaltenweise zur Technologie-MatrixA = (a1,a2, ? as) zusammen und führt den Spaltenvektor z = (z1,z2, ?,zs)T ein, dann ist die Technologie-Menge gegeben durch:
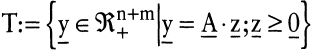
Die so definierte Technologie-Menge ist ein konvexer Kegel mit Spitze im Koordinatenursprung.
III. Ergebnisse der linearen Aktivitätsanalyse
Man kann zwei Entwicklungslinien der Aktivitätsanalyse unterscheiden, die beide in der grundlegenden Arbeit von Koopmans (Koopmans, T. C. 1951) vorgezeichnet sind: Der erste Lösungsansatz, der insb. von Debreu (Debreu, G. 1959) zur Begründung der modernen Mikroökonomie benutzt wurde, beruht auf der Theorie konvexer Kegel. Dieser Ansatz wird im deutschen Sprachraum insb. von Wittmann (Wittmann, W. 1966, Wittmann, W. 1968), Hildenbrand/Hildenbrand (Hildenbrand, H./Hildenbrand, W. 1975) vertreten. Wegen des engen Bezugs zur Produktionsplanung überwiegen im bwl. Bereich Ansätze auf der Grundlage der linearen Programmierung. In diesem Zusammenhang sind insb. die Arbeiten von Beckmann (Beckmann, M. J. 1955, Beckmann, M. J. 1960), Dorfman/Samuelson/Solow (Dorfmann, R./Samuelson, P. A./Solow, R. M. 1958), Baumol (Baumol, W. J. 1961), Albach (Albach, H. 1962) und Dano (Dano, S. 1966) zu erwähnen.
1. Lineare Aktivitätsanalyse und Produktionsfunktionen
Im Folgenden werden die Eigenschaften linearer Technologie-Mengen bzw. deren effizienter Rand mithilfe der parametrischen linearen Programmierung (vgl. Dinkelbach, W. 1969; Gal, T. 1973; Kistner, K.-P. 1993b) analysiert. Dabei wird wie folgt vorgegangen (vgl. Kistner, K.-P. 1981a; Kistner, K.-P. 1981b; Kistner, K.-P. 1993): Um einen Punkt des effizienten Randes zu bestimmen, formuliert man ein lineares Programm, in dem die Ausbringungsmenge eines Produkts maximiert bzw. die Einsatzmenge eines Faktors minimiert wird, wobei die Mengen aller anderen Güter konstant gehalten werden:
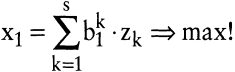
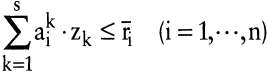 (LP1) (LP1)
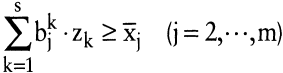
zk ≥ 0 (k = 1, ?,s)
bzw.
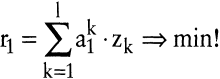
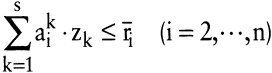 (LP2) (LP2)
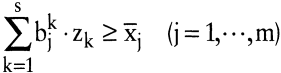
zk ≥ 0 (k = 1, ?,s)
In (LP1) und (LP2) bezeichnen die Indizes k = 1, ?,s die Produktionsprozesse, i = 1, ?,n die Faktoren und j = 1, ?,m die Produktarten. Die Konstanten aik symbolisieren die Produktionskoeffizienten, bik die Koppelungskoeffizienten, r¯i die verfügbaren Faktorbestände und x¯j die vorgegebenen Ausbringungsmengen. Die Variablen zk geben die Prozessniveaus an, r1 ist gleich der Einsatzmenge des variablen Faktors, und x1 ist gleich der Ausbringungsmenge des variablen Produkts.
Wegen der Möglichkeit der Verschwendung können in (LP1) und (LP2) die Restriktionen als Ungleichungen formuliert werden.
Für vorgegebene Faktorbestände und Ausbringungsmengen liefert die optimale Lösung von (LP1) bzw. (LP2) jeweils einen Punkt des effizienten Randes. Durch parametrische Variation der Beschränkungskonstanten kann man den effizienten Rand der Technologiemenge, der als Produktionsfunktion zu interpretieren ist, konstruieren. Insb. können durch parametrische Variation jeweils einer Konstanten achsenparallele Schnitte durch die Technologiemenge konstruiert werden, die grafisch als Konturlinien darstellbar sind. Diese entsprechen den Konturlinien des »Ertragsgebirges« der neoklassischen funktionalistischen Produktionstheorie.
Mithilfe allgemeiner Eigenschaften parametrischer linearer Programme werden im Folgenden die Eigenschaften neoklassischer Produktionsfunktionen aus den Annahmen der linearen Aktivitätsanalyse hergeleitet.
Zunächst wird in (LP1) die Einsatzmenge ri eines Faktors i variiert. Die sich so ergebende Konturlinie gibt die Abhängigkeit der Ausbringungsmenge x1 des variablen Produkts von der Einsatzmenge ri des zu variierenden Faktors (bei Konstanz der übrigen Gütermengen) an. Sie entspricht damit der Produktionsfunktion bei partieller Faktorvariation der neoklassischen Produktionstheorie. Da sie durch parametrische Variation der Beschränkungskonstanten einer Restriktion vom Typ »kleiner oder gleich« in einem Maximierungsproblem konstruiert wird, ist sie eine stückweise lineare, nicht fallende konkave Funktion, deren Anstieg in einer endlichen Zahl von kritischen Punkten sprunghaft fällt (vgl. Abb. 2a). Sieht man davon ab, dass diese Funktion in den kritischen Punkten nicht differenzierbar ist, dann lässt sich für lineare Technologien das Ertragsgesetz als ein Gesetz nicht zunehmender Ertragszuwächse formulieren.
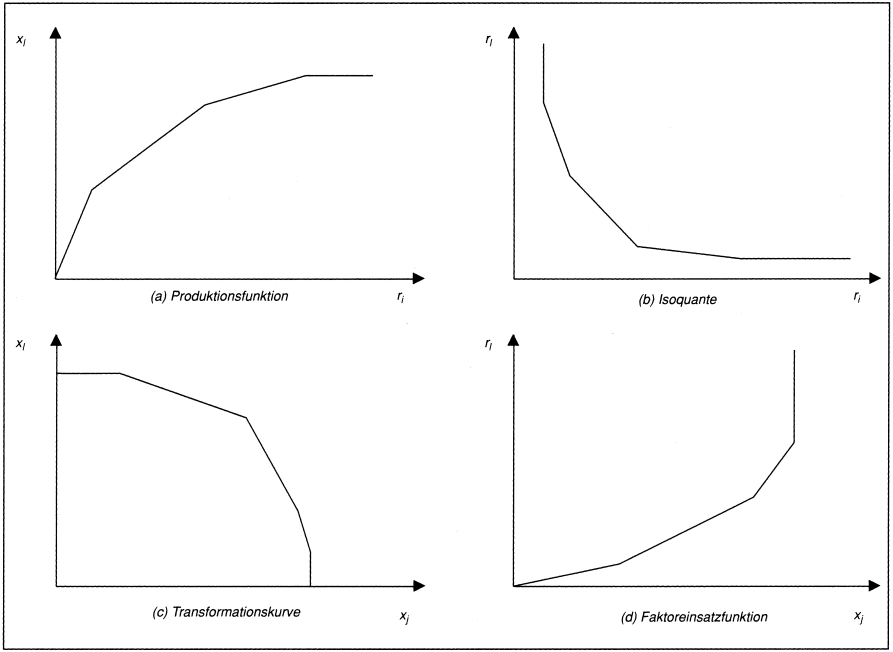
Abb. 2: Konturlinien bei linearen Technologien
Variiert man in (LP2) die Einsatzmenge ri eines Faktors i ≠ 1 parametrisch, dann gibt die Konturlinie die Abhängigkeit der mindestens benötigten Einsatzmenge r1 des Faktors 1 von der Einsatzmenge ri des Faktors i (bei Konstanz der übrigen Gütermengen) an. Sie entspricht damit der Isoquante der neoklassischen Produktionstheorie. Da (LP2) ein Minimierungsproblem mit Restriktionen vom Typ »kleiner oder gleich« ist, ist sie eine stückweise lineare, nicht steigende konvexe Funktion (vgl. Abb. 2b). Weil die Grenzrate der Substitution gleich dem (mit – 1 multiplizierten) Anstieg der Isoquante ist, gilt für lineare Technologien – wie bei neoklassischen Produktionsfunktionen – ein Gesetz nicht zunehmender Grenzraten der Faktor Substitution.
Zur Analyse der Austauschbeziehungen zwischen verschiedenen Produkten kann man in (LP1) die Ausbringungsmenge xj eines Produkts j ≠ 1 parametrisch variieren. Da es sich um ein Maximierungsproblem mit Restriktionen vom Typ »größer oder gleich« handelt, ist die Konturlinie stückweise linear, nicht steigend und konkav (vgl. Abb. 2c). Sie entspricht der Transformationskurve der neoklassischen Produktionstheorie. Aus der Konkavität der Konturlinie ergibt sich das Gesetz von der nicht abnehmenden Grenzrate der Produkt-Substitution.
Die Konturlinie bei parametrischer Variation der Ausbringungsmenge xj eines Produkts j ≠ 1 in (LP2) kann als Faktoreinsatzfunktion interpretiert werden (vgl. Abb. 2d). Sie ist gleich der Inversen der Produktionsfunktion bei partieller Faktorvariation und damit stückweise linear, nicht fallend und konvex.
Der effiziente Rand einer linearen Technologie bzw. die Produktionsfunktion besitzt im Wesentlichen die für neoklassische Produktionsfunktionen vorausgesetzten Eigenschaften. Die Konturlinien sind allerdings nicht glatt, sondern stückweise linear; an die Stelle zunehmender bzw. abnehmender Austauschraten zwischen den einzelnen Güterarten treten nicht abnehmende bzw. nicht zunehmende Austauschraten. Die wesentlichen Konvexitätseigenschaften von Produktionsfunktionen bleiben jedoch erhalten.
Diese Ergebnisse lassen sich auch auf den Fall übertragen, dass nicht nur die Mengen einzelner Güterarten variiert werden, sondern die Einsatzmengen ganzer Güterpakete proportional variiert werden. Von besonderem Interesse ist hierbei die Variation der Einsatzmengen aller Faktoren. Im Fall eines einzigen Produktes führt dieses wegen der Proportionalität linearer Technologien zu einer proportionalen Erhöhung der Ausbringungsmenge: Die Produktionsfunktion bei totaler Faktorvariation ist linearhomogen bzw. besitzt konstante Skalenerträge.
Im Fall mehrerer Produkte kann man in (LP1) die Ausbringungsmenge xj der Produkte j = 2, ?,m konstant halten und die Einsatzmengen ri aller Faktoren i = 1, ?,n proportional variieren. Da nicht alle Restriktionskonstanten variiert werden, kommt die Proportionalität nicht zum Tragen, vielmehr ist dann die Produktionsfunktion bei totaler Faktorvariation eine stückweise lineare, nicht fallende, konkave Funktion; sie besitzt nicht zunehmende Skalenerträge. Die Ausbringungsmenge x1 kann allerdings von einem bestimmten Punkt an proportional mit den Einsatzmengen aller Faktoren ansteigen.
2. Effizienzpreis-Theorem
Die Beziehung zwischen dem Effizienzbegriff und der Gewinnmaximierung wird durch das Effizienzpreis-Theorem hergestellt.
Satz: Effizienzpreis-Theorem von Koopmans
Eine Aktivität y˚ = (r˚,x˚) ist genau dann effizient, wenn es mindestens ein System von positiven Faktorpreisen q˚ und Produktpreisen p˚ gibt, für das y˚ den Gewinn maximiert, d.h.
Go = po′ · xo – qo′ · ro ≥ po′ · x – qo′ · r
für alle y = (r,x) ∊ T
Jeder effizienten Aktivität kann also ein Preissystem zugeordnet werden, das den Gewinn maximiert; umgekehrt kann man zu jedem Preissystem eine Aktivität angeben, die bei diesen Preisen den Gewinn maximiert. Der Beweis wurde von Koopmans (Koopmans, T. C. 1951, S. 61 ff.) mithilfe der Theorie der konvexen Kegel geführt; ein bwl. intuitiverer Beweis beruht auf dem Preistheorem der LP (vgl. Kistner, K.-P. 1993a, S. 119).
IV. Erweiterte Technologien ohne Verschwendung
Im Einprodukt-Fall lässt sich die Annahme der Möglichkeit der Verschwendung durch eine geeignete Interpretation rechtfertigen: Eine Verschwendung von Maschinenkapazitäten und Arbeitskräften bedeutet, dass diese in der Planungsperiode nur teilweise genutzt werden; die Verschwendung von Werkstoffen kann als Einlagern interpretiert werden. Diese Interpretation kann jedoch nicht auf den Mehrprodukt-Fall übertragen werden: Wenn mit einem Produktionsprozess mehrere Produkte erzeugt werden, stehen deren Ausbringungsmengen in einem festen Verhältnis zueinander; es liegt also der Fall der Kuppelproduktion vor. Können Kuppelprodukte nicht verkauft oder produktiv eingesetzt werden, dann müssen sie – meist unter Einsatz von Produktionsfaktoren – entsorgt werden, d.h. vernichtet oder in andere Stoffe umgewandelt bzw. unter Inanspruchnahme der Dienstleistungen von Entsorgungsunternehmen beseitigt werden.
Hieraus könnte geschlossen werden, dass die lineare Aktivitätsanalyse wegen unerwünschter Kuppelprodukte, die nicht verschwendet werden können, ungeeignet ist, die Bedingungen der betrieblichen Produktion angemessen zu berücksichtigen. Bereits Koopmans (Koopmans, T. C. 1951) hat jedoch darauf hingewiesen, dass Kuppelprodukte in der Aktivitätsanalyse berücksichtigt werden können, indem man das Ergebnis der Produktion in erwünschte Güter bzw. Produkte und unerwünschte Güter oder Redukte (Dyckhoff, H. 1994) aufteilt. Unerwünschte Produkte müssen unter Einsatz von Produktionsfaktoren beseitigt oder in andere, erwünschte Güter transformiert werden. Dieser Vorgang wird durch Entsorgungsaktivitäten abgebildet, die unerwünschte Güter unter Einsatz von positiven Faktormengen vernichten oder auch in erwünschte Güter transformieren.
1. Die erweiterte Technologie-Menge
Um eine solche erweiterte Technologie-Menge formal darzustellen, werden folgende Symbole eingeführt:
t = 1, ?,τ: unerwünschte Güter; ut: deren Ausbringungsmengen. wtk: Outputkoeffizienten für die Güter t = 1, ?,τ in den Produktionsprozessen k = 1, ?,s. h = 1, ?,ν: Reduktionsprozesse zur Vernichtung unerwünschter Güter. vh: Niveau-Vektor für Reduktionsprozesse. cih: Inputkoeffizienten für Einsatz der Faktoren i = 1, ?,n in den Reduktionsprozessen h = 1, ?,ν. gjh: Outputkoeffizienten für die Ausbringung der erwünschen Güter j = 1, ?,m durch die Reduktionsprozesse h = 1, ?,v. dth: Koeffizienten, die angeben in welchem Umfang die unerwünschten Güter t = 1, ?,τ durch die Reduktionsprozesse h = 1, ?,ν vernichtet werden; da es möglich ist, dass bei der Reduktion eines unerwünschten Gutes ein anderes unerwünschtes Gut entsteht, können einzelne dieser Koeffizienten negativ sein.
Dann kann man die erweiterte Technologie-Menge durch folgendes lineares Gleichungssystem beschreiben:
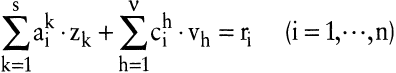
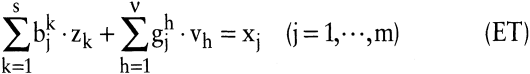
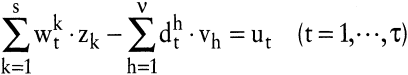
Alle Aktivitäten, d.h. alle Güterkombinationen y = (r,u,x), die dem Gleichungssystem (ET) genügen, gehören zur erweiterten Technologie-Menge.
Das Effizienzkriterium lässt sich wie folgt auf erweiterte Technologien übertragen:
Definition: Effizienzkriterium für erweiterte Technologien
Eine Aktivität y˚ = (r˚,u˚,x˚) ∊ T heißt effizient, falls es keine andere Aktivität y = (r,u,x) ∊ T gibt, sodass r˚ ≥ r; u˚ ≥ u; x˚ ≤ xund ri˚ > ri für mindestens einen Faktor i oder ut˚ > ut für mindestens ein unerwünschtes Gut t oder xj < xj für mindestens ein Produkt j.
2. Eigenschaften der erweiterten Technologie
Um den effizienten Rand der erweiterten Technologie mithilfe der parametrischen linearen Programmierung analysieren zu können, wird eine zulässige Ausgangsaktivität y¯ mit vorgegebenen Faktoreinsatzmengen r¯, vorgegebenen Mengen u¯ der unerwünschten Güter und vorgegebenen Ausbringungsmengen x¯ der Produkte betrachtet. Um Konturlinien für den effizienten Rand der Technologie-Menge bzw. Austauschbeziehungen zwischen einzelnen Gütern herzuleiten, wird dann die Menge jeweils eines Gutes maximiert bzw. minimiert und die Menge eines anderen parametrisch variiert. Da eine Unterschreitung der vorgegebenen Einsatzmenge eines Faktors bzw. der Ausbringungsmenge eines unerwünschten Gutes und die Überschreitung der Ausbringungsmenge eines Produktes erwünscht sind, können in (ET) die Gleichungen durch Ungleichungen ersetzt werden:
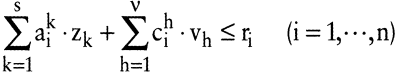
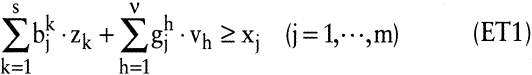
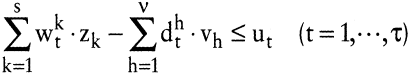
Wegen der Eigenschaften parametrischer linearer Programme treten auch bei erweiterten Technologien nur die in Abb. 2 wiedergegebenen Formen der Konturlinien auf. Es ergeben sich daher die in Tab. 1 dargestellten Typen.

Tab. 1: Typen von Konturlinien bei erweiterten Technologien
Für erweiterte Technologien gilt weiter:
Satz: Effizienzpreis-Theorem für erweiterte Technologien
Eine Aktivität yo = (ro,uo,xo) ist genau dann effizient, wenn es mindestens ein System von positiven Faktorpreisen qo, Produktpreisen po und Bewertungen von unerwünschten Gütern ωo gibt, für das yo den Gewinn maximiert, d.h.
Go = po′ · xo – qo′ · ro – ωo′ · uo ≥ po′ · x – qo′ · r – ωo′ · u
für alle y = (r,x) ∊ T
Als Ergebnis ist festzuhalten, dass es möglich ist, die wesentlichen Ergebnisse der linearen Aktivitätsanalyse auf erweiterte Technologien mit unerwünschten Produkten und Reduktionsaktivitäten zu übertragen.
3. Umwelteinflüsse der Produktion und Aktivitätsanalyse
Interpretiert man unerwünschte Kuppelprodukte als Schadstoffe, Begrenzungen der Ausbringung unerwünschter Güter als Emissionsgrenzen und Reduktionsprozesse als Maßnahmen des betrieblichen Umweltschutzes, dann lassen sich auch ökologische Aspekte in der Produktionstheorie erfassen.
Die Übertragung der Theorie der Kuppelproduktion auf die Analyse ökologischer Auswirkungen der Produktion wurde von Schmidtchen (Schmidtchen, D. 1980) angeregt und von Kistner (Kistner, K.-P. 1983, Kistner, K.-P. 1989, Kistner, K.-P. 1993) mit der Analyse erweiterter Technologien verbunden. Ein ähnlicher Ansatz findet sich bei Dinkelbach (Dinkelbach, W. 1991) und Dyckhoff (Dyckhoff, H. 1991, Dyckhoff, H. 1993, Dyckhoff, H. 1994). Dinkelbach/Piro (Dinkelbach, W./Piro, A. 1989) beziehen das betriebliche Recycling explizit in die Analyse ein. Eine geschlossene Theorie von Produktion und Umweltschutz, in der u.a. das Konzept der erweiterten Technologien konsequent auf ökologische Aspekte der Produktion angewendet wird, wurde von Steven (Steven, M. 1994) entwickelt.
Als Ergebnis ist festzustellen, dass durch das Konzept der erweiterten Technologien ökologische Fragen in die herkömmliche Produktionstheorie integriert werden können.
Literatur:
Albach, H. : Zur Verbindung von Produktionstheorie und Investitionstheorie, in: Zur Theorie der Unternehmung, hrsg. v. Koch, H., Wiesbaden 1962
Baumol, W. J. : Economic Theory and Operations Analysis, Englewood Cliffs/N.J. 1961
Beckmann, M. J. : Grundbegriffe der Produktionstheorie vom Standpunkt der Aktivitätsanalyse, in: Weltwirtschaftliches Archiv, 1955, S. 33 – 58
Beckmann, M. J. : Lineares Programmieren und neoklassische Theorie, in: Weltwirtschaftliches Archiv, 1960, S. 39 – 52
Dano, S. : Industrial Production Models, Wien 1966
Debreu, G. : Theory of Value: An Axiomatic Analysis of Economic Equilibrium, New York 1959
Dinkelbach, W. : Sensitivitätsanalysen und parametrische lineare Programmierung, Berlin et al. 1969
Dinkelbach, W. : Effiziente Produktionen in umweltorientierten Leontief-Technologien, in: Operations Research, hrsg. v. Fandel, G./Gehring, H., Berlin et al. 1991, S. 361 – 375
Dinkelbach, W./Piro, A. : Entsorgung und Recycling in der bwl. Produktions- und Kostentheorie: Leontief-Technologien, in: wisu, 1989, S. 399 – 405 u. 474 – 480
Dinkelbach, W./Rosenberg, O. : Erfolgs- und umweltorientierte Produktionstheorie, Berlin et al. 1994
Dorfman, R./Samuelson, P. A./Solow, R. M. : Linear Programming and Economic Analysis, New York 1958
Dyckhoff, H. : Berücksichtigung des Umweltschutzes in der bwl. Produktionstheorie, in: Betriebswirtschaftslehre und Ökonmische Theorie, hrsg. v. Ordelheide, D./Rudolph, B./Büsselmann, E., Stuttgart 1991, S. 275 – 309
Dyckhoff, H. : Aktivitätsanalytische Grundlagen einer umweltorientierten einzelwirtschaftlichen Produktions- und Erfolgstheorie, in: Z. f. Wirtschafts- u. Sozialwissenschaften, 1993a, S. 3 – 16
Dyckhoff, H. : Aktivitätsanalyse, in: HWB, hrsg. v. Wittmann, W./Kern, W./Köhler, R. et al., 5. A., Stuttgart 1993b, S. 57 – 68
Dyckhoff, H. : Betriebliche Produktion, 2. A., Berlin et al. 1994
Fandel, G. : Betriebliche Produktion I, 3. A., Berlin et al. 1991
Gal, T. : Betriebliche Entscheidungsprobleme, Sensitivitätsanalyse und parametrische Programmierung, Berlin 1973
Hildenbrand, H./Hildenbrand, W. : Lineare ökonomische Modelle, Berlin et al. 1975
Kistner, K.-P. : Produktions- und Kostentheorie (1. A., Würzburg 1981a), 2. A., Heidelberg 1993a
Kistner, K.-P. : Aktivitätsanalyse, lineare Programmierung und neoklassische Produktionstheorie, in: WiSt, 1981b, S. 145 – 151
Kistner, K.-P. : Zur Erfassung von Umwelteinflüssen in der linearen Aktivitätsanalyse, in: WiSt, 1983, S. 389 – 395
Kistner, K.-P. : Zur Erfassung von Umwelteinflüssen in der betrieblichen Produktionsplanung, in: BFuP, 1989, S. 30 – 50
Kistner, K.-P. : Optimerungsmethoden, 2. A., Heidelberg 1993b
Koopmans, T. C. : Analysis of Production as an Efficient Combination of Activities, in: Activity Analysis of Production and Allocation, hrsg. v. Koopmans, T. C., New York 1951, S. 33 – 97
Schmidtchen, D. : Theorie der Kuppelproduktion nebst einer Anwendung auf den Umweltschutz, in: wisu, 1980, S. 287 – 290 u. 335 – 343
Steven, M. : Produktion und Umweltschutz, Wiesbaden 1992
Wittmann, W. : Grundzüge einer axiomatischen Produktionstheorie, in: Produktionstheorie und Produktionsplanung, hrsg. v. Moxter, A./Schneider, D./Wittmann, W., Köln et al. 1966, S. 9 – 36
Wittmann, W. : Produktionstheorie, Berlin et al. 1968
|