|
Prognosemethoden, quantitative
Inhaltsübersicht
I. Grundlagen
II. Prognosemethoden auf der Basis univariater Modelle
III. Methoden auf der Basis multivariater Modelle
IV. Ausblick: Die zunehmende Bedeutung quantitativer Prognosemethoden für die Unternehmensrechnung und das Controlling
I. Grundlagen
1. Begriff und Merkmale
Unter Prognosemethoden wird die systematische Vorgehensweise zur Ermittlung von Prognosen sowie die Herleitung von Aussagen über zukünftige Entwicklungen und Ereignisse auf der Basis von Beobachtungen und Hypothesen, die aus Theorien abgeleitet werden, verstanden. Am häufigsten wird als Grundlage für die Erstellung einer Prognose eine Zeitreihe verwendet, die als Menge der im zeitlich gleichen Abstand beobachteten Werte der Vergangenheit definiert ist. Durch die Analyse der Zeitreihe sollen Gesetzmäßigkeiten aufgedeckt und für die Prognose verwendet werden. Eine wesentliche Voraussetzung für diese Vorgehensweise ist die Zeitstabilitätshypothese, die davon ausgeht, dass die vermuteten Gesetzmäßigkeiten auch für die zukünftigen Entwicklungen Geltung haben werden. Grundsätzlich können Prognosemethoden in qualitative und quantitative Methoden unterschieden werden, wobei die qualitativen Prognosemethoden qualitativen Methoden heuristische Prognosen erarbeiten und vorwiegend qualitativ argumentieren. Die quantitativen Methoden dagegen verwenden grundsätzlich mathematische Methoden zur Ermittlung der Prognose.
2. Durchführung und Anwendungsbereiche
Die quantitativen Methoden können grundsätzlich in Zeitreihenanalysen und Kausalmodelle unterschieden werden. Während Zeitreihenanalysen im Rahmen der kurz- und mittelfristigen Planung ihre Anwendung vor allem in der Vorhersage von Saisonschwankungen, zyklischen Änderungen, Trends und Wachstumsentwicklungen finden, werden Kausalmodelle vorwiegend bei der langfristigen Planung eingesetzt, wenn Kausalbeziehungen vermutet werden oder bekannt sind.
Um eine Prognosemethode auswählen zu können, muss der Prognosegegenstand festgelegt werden, es muss ein Erklärungsmodell für den Prognosegegenstand formuliert werden, es muss eine Untersuchung der Zeitstabilitätshypothese erfolgen, die abhängigen und unabhängigen Variablen müssen auf ihre Messbarkeit hin überprüft werden, Zeitreihen müssen untersucht und das Erklärungsmodell muss gestestet werden. Nach Anwendung der Prognosemethoden ist es abschließend erforderlich, die Ergebnisse auf ihre Aussagekraft und Validität hin kritisch zu überprüfen und im Rahmen einer ex-post Abweichungsanalyse die zugrunde liegenden Hypothesen einer kritischen Würdigung zu unterziehen.
II. Prognosemethoden auf der Basis univariater Modelle
Wird eine Prognose ausschließlich aus den Vergangenheitsdaten der Zeitreihe abgeleitet, so spricht man von univariaten Modellen. Zu den Prognosemethoden, die auf univariaten Modellen beruhen, rechnet man die Methode der gleitenden Durchschnitte, die Methode der exponentiellen Glättung, die Methoden der Prognose bei Saisonzyklen, die Methode der Trendextrapolation, die autoregressiven Verfahren sowie die Methoden, die Wachstums- oder Sättigungsmodelle verwenden (Brockwell, P.J./Davis, R.A. 1998).
Bei der Methode der gleitenden Durchschnitte erhält man den Prognosewert als das arithmetische Mittel der letzten n Zeitreihenwerte. Je größer die Zahl n der berücksichtigten Zeitreihenwerte ist, umso langsamer werden Niveauveränderungen der zu prognostizierenden Größe nachvollzogen und umso mehr werden zufällige Schwankungen des beobachteten Wertes ausgeglichen.
Die Methode der exponentiellen Glättung berücksichtigt nicht nur die letzten n Zeitreihenwerte, sondern alle beobachteten Realisationswerte. Sie gewichtet jedoch die älteren Beobachtungswerte exponentiell geringer als die jüngeren. Bezeichnet man mit xt den aktuellen Wert der Zeitreihe und mit yt den Prognosewert für den Zeitpunkt t, so wird bei der exponentiellen Glättung der Prognosewert yt+1 wie folgt ermittelt:
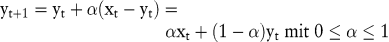
Rekursives Einsetzen führt zu der Gleichung
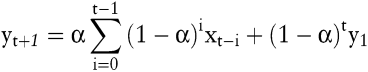
Die Prognosemethoden gleitender Durchschnitt und exponentielle Glättung sind grundsätzlich nur zur Prognose von solchen Größen geeignet, die keinem Trend folgen. Bei einem steigenden Trend würden diese beiden Methoden systematisch einen zu geringen Prognosewert ergeben und bei einem sinkenden Trend einen zu hohen. Will man mit diesen beiden Verfahren eine Größe prognostizieren, die einem linearen Trend folgt, so ist es zweckmäßig, die als gleich bleibend erwarteten Steigerungsraten zu prognostizieren.
Eine andere Möglichkeit, einen linearen Trend zu berücksichtigen, bietet die exponentielle Glättung zweiter Ordnung, die zu folgender Gleichung führt:
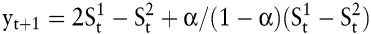
mit
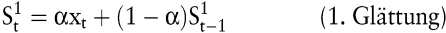
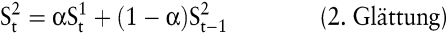
Kritisch anzumerken an diesen in der Praxis aufgrund ihrer relativ geringen Anwendungsvoraussetzungen und leichten Programmierbarkeit häufig eingesetzten Verfahren sind die ausschließliche Berücksichtigung der Zeit als Einflussfaktor, der subjektiv festzulegende Glättungsparameter α und die für praktische Anwendungszwecke nicht immer geeignete Gewichtung der Zeitreihenwerte.
2. Prognosemethoden bei Saisonzyklen (Saisonverfahren)
Saisonverfahren basieren auf der Analyse von Zeitreihen mit zyklischen Schwankungen und können grob in zwei Klassen unterteilt werden. Die erste Klasse von Verfahren nimmt eine Saisonbereinigung auf der Grundlage der gleitenden Durchschnitte oder der exponentiellen Glättung vor, die zweite Klasse von Verfahren bildet die Saisonkomponente durch eine Sinus- bzw. Cosinusfunktion nach.
Zu den Saison-Prognosemethoden zählt man das ursprüngliche Bundesbankverfahren, die Census-Methode II und die Methode von Winter. Bei diesen Verfahren wird in einem ersten Schritt der gleitende Durchschnitt für einen vollständigen Saisonzyklus ermittelt. Für jede Teilperiode wird sodann der Zeitreihenwert durch diesen gleitenden Durchschnitt dividiert und der Saisonindex zur Bereinigung der Zeitreihe ermittelt. Mit der exponentiellen Glättung werden die saisonalen Abweichungen einer Zeitreihe von ihrem Durchschnittswert durch einen Saisonfaktor berücksichtigt, der sich aus dem Quotienten zwischen dem tatsächlichen Zeitreihenwert und dem Jahresdurchschnittswert ergibt. (Hansmann, K.-W. 1983, S. 46 ff.)
Zu den Verfahren der zweiten Klasse zählen die Spektralanalyse und die Berliner Verfahren. Mit Hilfe von Fourier-Transformationen wird eine Übertragung der Zeitreihe in einen Frequenzbereich vorgenommen, die eine zeitunabhängige Identifizierung von sich überschneidenden Saisonzyklen ermöglicht. Die Identifizierung erfolgt durch die Zerlegung der Varianz einer Zeitreihe in mehrere additive Komponenten und deren Zuordnung zu den sich überschneidenden Saisonzyklen. Die Erfahrung zeigt freilich, dass der relativ hohe mathematische Aufwand für eine Spektralanalyse durch die Güte der Prognose häufig nicht gerechtfertigt wird (Shumway, R.H./Stoffer, D.S. 2000, S. 213 ff.).
3. Methode der Trendextrapolation (einfache Regressionsanalyse)
Die Grundidee der Trendextrapolation (einfache Regressionsanalyse) basiert darauf, die beobachteten Zeitreihenwerte durch ein Polynom, dessen einzige unabhängige Variable die Zeit t ist, abzubilden. Für die Darstellung eines linearen Trends wird das Polynom xt = a0 + a1t + ut mit ut als zufallsabhängige Störgröße angesetzt. Die Parameter a0 und a1 ergeben sich mit Hilfe der Methode der kleinsten Quadrate, nach der die Summe der quadrierten Abweichungen zwischen den eingetretenen Zeitwerten und den Werten des Polynoms minimiert wird, aus den folgenden Normalgleichungen:
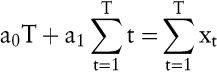
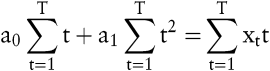
Bei Erfüllung der Zeitstabilitätshypothese dient das Polynom als Prognosegleichung für die zukünftigen Zeitreihenwerte und kann in die Zukunft extrapoliert werden. Polynome mit einem höheren Grad als zwei können bei einer Extrapolation durch ihre hohe Steigung zu extremen Prognosewerten führen und sollten deshalb nur in begründeten Fällen verwendet werden.
4. Autoregressive Verfahren
Autoregressive Verfahren leiten den Prognosewert aus den Vergangenheitswerten regressionsähnlich ab und versuchen, die Gewichte individuell für jeden beobachteten Wert zu optimieren. Die exponentielle Glättung stellt in diesem Kontext nur noch einen Speziallfall dar. Das Problem stellt sich in der Schätzung der Parameter a0,...,ap, die maßgeblich die angesetzte Grundgleichung bestimmen:
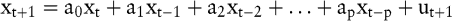
Die Variable ut+1 ist eine zufallsabhängige Störvariable und p ist die Ordnung des zugrunde liegenden autoregressiven Prozesses, die so gewählt werden muss, dass eine befriedigende Approximation von xt+1 erreicht wird. Die Grundgleichung wird autoregressiver Prozess p-ter Ordnung (AR(p)-Prozess) genannt. Für die Schätzung der Parameter a0,...,ap werden in der Literatur vorwiegend zwei mathematische Verfahren, und zwar das Box-Jenkins-Verfahren und das Verfahren adaptiver Filter, eingesetzt.
Beim Box-Jenkins-Verfahren wird jeder Zeitreihenwert als Summe der gewichteten vergangenen Zeitreihenwerte zuzüglich einer Störvariablen ermittelt. Um zu überprüfen, ob eine konkret zu untersuchende Zeitreihe einem autoregressiven Prozess eines bestimmten Grades entspricht, und um die Parameter a0,...,ap schätzen zu können, wird zunächst die Autokorrelationsfunktion rτ (τ = 1,2,...) formuliert, in der τ die zeitliche Verzögerung, den time lag, angibt:
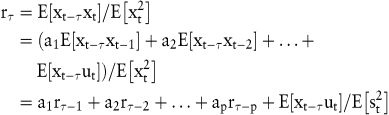
Nach Aufstellung aller Autokorrelationsfunktionen für τ = 1,2,...,p ergibt sich ein lineares Gleichungssystem mit p Gleichungen, die auch Yule-Walker-Gleichungen genannt werden, und für die aufgrund der Symmetrie des time lags die Eigenschaften r0 = 1 und r – i = ri gelten müssen. Bei einem AR(p)-Prozess sind die Parameter a1 bis ap ungleich Null und danach gleich Null, sodass man die Ordnung p des Prozesses ermitteln kann, indem man p die Werte 1, 2, ... durchlaufen lässt und die entstehenden Gleichungssysteme so lange löst, bis ap den Wert Null annimmt.
Von einem Moving-Average-Prozess q-ter Ordnung (MA(q)-Prozess) wird gesprochen, wenn die folgende Gleichung vorliegt, bei welcher der Zeitreihenwert xt durch die Vergangenheitswerte der Störvariablen ausgedrückt wird:
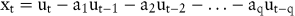
Die eventuell irritierende Bezeichnung Moving-Average rührt daher, dass ein endlicher MA(q)-Prozess durch eine unendliche Reihe gewogener Vergangenheitswerte der Zeitreihe approximiert wird und somit xt als gewogener Durchschnitt der Vergangenheitswerte dargestellt werden kann. Das zu lösende Gleichungssystem ist bei diesem Ansatz allerdings nichtlinear und daher nur iterativ oder mit Hilfe von Taylorentwicklungen lösbar. Mit der Kombination der beiden Prozesse zu einem so genannten ARMA(p,q)-Prozess (Autoregressive Moving-Average) kann eine Verbesserung der Prognose erzielt werden. Die Anwendung dieser Kombination ist allerdings auf stationäre Zeitreihen beschränkt und sie erfordert die Transformation nichtstationärer in stationäre Zeitreihen. Liegt eine Zeitreihe mit einem linearen Trend vor, so kann diese durch die Differenzbildung xt – xt-1 in eine stationäre Zeitreihe umgeformt und das Box-Jenkins-Verfahren angewendet werden. Abschließend erfolgt eine Rücktransformation dieser stationären Zeitreihe in die ursprüngliche nichtstationäre Zeitreihe. Nichtstationäre Zeitreihen dieser Art werden auch Autoregressive Integrated Moving Average-Prozess (ARIMA) genannt (Shumway, R.H./Stoffer, D.S. 2000, S. 144 ff.).
Beim adaptiven Filtern wird dieselbe Prognosegleichung wie beim Box-Jenkins-Verfahren verwendet. Die Parameter werden allerdings nicht mit einem nichtlinearen Gleichungssystem, sondern mit einer linearen Approximation des Gradienten der Zielfunktion geschätzt. Die Schnelligkeit der resultierenden dynamischen Anpassungsfunktionen wird durch eine Lernkonstante K gesteuert, die vom Entscheidungsträger subjektiv festgelegt werden muss, und daher mit einer gewissen Unsicherheit behaftet ist:
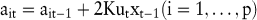
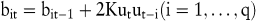 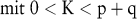
5. Wachstums- und Sättigungsmethoden
Sättigungsmodelle dienen der Prognose eines langfristigen Trends einer Zeitreihe, deren Werte nichtlinear verlaufen und einem Sättigungsniveau zustreben, wie z.B. bei einer Marktsättigung. Für die mathematische Darstellung dieses Verlaufs bieten sich die logistische Funktion und die Gompertz-Funktion an.
Die logistische Funktion unterstellt für den Verlauf der betrachteten Zeitreihe, dass deren Wachstum proportional zu dem im Zeitpunkt t erreichten Niveau x(t) und zu der Differenz zwischen dem erreichten Niveau x(t) und dem absoluten Sättigungsniveau S ist. Formal lassen sich diese beiden Eigenschaften wie folgt ausdrücken:
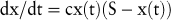
In dieser Formel ist c ein Proportionalitätsfaktor und dx/dt ist das Wachstum der Zeitreihe pro Zeiteinheit. Integration und Umformen dieser Wachstumsgleichung führen zur logistischen Funktion
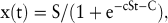
in der die Parameter S, c und C aus Vergangenheitsdaten der Zeitreihe geschätzt werden müssen.
Ähnlich wie die logistische Funktion unterstellt die Gompertz-Funktion für das Wachstum der Zeitreihe pro Zeiteinheit, dass es proportional zu dem im Zeitpunkt t erreichten Niveau x(t) und zur logarithmischen Differenz des absoluten Sättigungsniveaus S und vom Niveau x(t) ist. Hieraus ergibt sich die Gompertz-Funktion als:
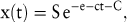
in der ebenfalls die Parameter S, c und C aus Vergangenheitsdaten der Zeitreihe geschätzt werden müssen.
III. Methoden auf der Basis multivariater Modelle
Wird die Prognose der zu prognostizierenden Variablen nicht aus ihren vergangenen Werten (Zeitreihe), sondern aus anderen Variablen, welche mit der zu prognostizierenden Variablen durch eine Kausalitätsbeziehung verbunden sind, abgeleitet, so spricht man von multivariaten Verfahren. Das Erkennen von Kausalbeziehungen zwischen verschiedenen Zeitreihen beruht grundsätzlich nicht auf statistischen Auswertungen, sondern auf theoretischen Erkenntnissen. Sind die Kausalrichtungen bekannt, so können multivariate Verfahren eingesetzt und es kann das quantitative Ausmaß des Einflusses der Zeitreihen der unabhängigen Variablen auf die zu prognostizierende Variable mithilfe statistischer Methoden bestimmt werden. Zu den wichtigsten kausalen Prognoseverfahren zählen die Indikator-Methode, die multiple Regressionsanalyse sowie die Lebenszyklusanalyse.
1. Indikator-Methode und multiple Regressionsanaylse
Bei der Indikator-Methode als einfaches kausales Prognoseverfahren wird der zukünftige Wert einer ökonomischen Größe auf eine ihr zeitlich vorgelagerte Entwicklung zurückgeführt. So kann z.B. die Umsatzentwicklung eines Produktes in Abhängigkeit von der Anzahl der bislang eingegangenen Aufträge prognostiziert werden.
Bei der multiplen Regressionsanalyse werden dagegen mehrere exogene Variable berücksichtigt, von denen man aufgrund einer Theorie erwartet, dass sie die zu prognostizierende Variable beeinflussen. Für die Formulierung einer linearen Regressionsgleichung werden die Zeitreihen der exogenen Variablen benötigt:
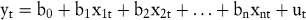
In dieser Gleichung sind yt die zu prognostizierenden Variablen, xit der Wert der exogenen Zeitreihe i zum Zeitpunkt t und ut ist die zufallsbedingte Störvariable im Zeitpunkt t. Die Regressionskoeffizienten bi repräsentieren den quantitativen Einfluss der exogenen Zeitreihe i auf die Entwicklung der zu prognostizierenden Variablen und werden mit der Methode der kleinsten Quadrate geschätzt und im Anschluss auf ihre Signifikanz überprüft.
Die Linearität der Regressionsfunktion stellt insbesondere für den Lösungsweg eine große Vereinfachung dar, weil so nur ein lineares Gleichungssystem aufzustellen und zu lösen ist. Soweit es erforderlich ist, können nichtlineare Funktionen in bestimmten Bereichen der Variablen linear approximiert und auf die obige Grundform transfomiert werden. Bei Funktionen, wie sie in den Wachstums- und Sättigungsmodellen üblich sind, erreicht man eine Linearisierung durch Logarithmieren.
2. Prognosen auf der Basis von Lebenszyklusmodellen
Der Lebenszyklus eines Produktes oder auch einer ausreichend genau definierten Produktgruppe wird in den Lebenszyklusmodellen regelmäßig in fünf Phasen eingeteilt. Mit der Einführung des Produktes beginnt die Einführungsphase und sie endet mit dem Erreichen der Gewinnschwelle, das heißt, wenn die Anlaufkosten durch die erzielten Erlöse erwirtschaftet worden sind. Es schließt sich die Wachstumsphase an, die durch einen Umsatzanstieg mit wachsenden Zuwachsraten gekennzeichnet ist und die endet, wenn die Wachstumsraten nicht mehr zunehmen. In der Reifephase steigt der Umsatz in seiner absoluten Höhe zwar weiter an, aber der Umsatzanstieg sinkt, was in der Regel die Folge einer zunehmenden Marktsättigung ist. Wenn der Umsatz nicht mehr steigt, sondern stagniert, geht die Reifephase in die Sättigungsphase über. Die Degenerationsphase folgt der Sättigungsphase, wenn der Umsatz abnimmt. Sie endet, wenn das Produkt aus dem Markt genommen wird.
Auf der Basis eines Modells über den Lebenszyklus eines Produktes können Umsatz, Absatz, Gewinn und auch andere Größen, wie z.B. Rentabilitäten, prognostiziert werden. Dazu ist es erforderlich, durch eine Markt- und Wettbewerbsanalyse festzustellen, in welcher Phase des Lebenszyklusses sich ein Produkt befindet und wie die Wettbewerbsposition des Produktes auf dem relevanten Markt ist. Zur konkreten Prognose von zukünftigen Umsätzen, Gewinnen usw. werden häufig die bereits dargestellten Methoden der linearen Trendextrapolation und die Wachstums- und Sättigungsmethoden (z.B. die logistische Funktion) angewandt.
3. Die Prognose des Ablaufs von Projekten mit Hilfe der Netzplantechnik
Die Netzplantechnik analysiert den Ablauf von komplexen, oft großen und innovativen Projekten und veranschaulicht den Projektablauf durch einen Netzplan. Im Netzplan werden alle Vorgänge (Aktivitäten), die insgesamt erledigt werden müssen, um das Projekt erfolgreich zu realisieren, in ihrer technologisch und organisatorisch bedingten Abhängigkeit aufgeführt. Prognostiziert man für jeden Vorgang seine Dauer, so ergibt der zeitlich längste Weg durch den Netzplan (kritischer Weg) eine Prognose für die Dauer des ganzen Projektes (Projektdauer).
Die Ausführung der einzelnen Vorgänge zur Realisierung des Projektes erfordert den Einsatz von Ressourcen, vor allem von Personal und Finanzmitteln. Prognostiziert man für die einzelnen Vorgänge ihren Bedarf an Ressourcen, dann kann man mithilfe der Netzplantechnik Prognosen über die Entwicklung des Ressourcenbedarfs im Laufe der Realisierung des Projektes, insbesondere des Personalbedarfs und des Bedarfes an finanziellen Mitteln, erarbeiten. Die Grundlage für solche Prognosen sind die Kapazitäts- und Beschäftigungsplanung sowie die Finanzplanung im Rahmen der Netzplantechnik.
IV. Ausblick: Die zunehmende Bedeutung quantitativer Prognosemethoden für die Unternehmensrechnung und das Controlling
Im Rahmen der Unternehmensrechnung und des Controllings werden Informationen erarbeitet, die bestimmte Entscheidungsträger, wie z.B. die Unternehmensleitung oder die Anteilseigner, für ihre Entscheidungen benötigen. Diese entscheidungsrelevanten Informationen bestehen zu einem Teil aus Beobachtungen und Berichten über Abläufe und Begebenheiten in der Vergangenheit und sie bestehen zu einem zweiten sehr wesentlichen Teil aus qualitativen Prognosemethoden und quantitativen Prognosen über die zu erwartenden Entwicklungen und über zu erwartende Ereignisse. Die Qualität der Entscheidungen ist in hohem Maße abhängig von der Qualität der Informationen, insbesondere von der Qualität der Prognosen, auf denen die Entscheidungen beruhen. Soweit Sachverhalte nicht quantifiziert werden können, ist man auf qualitative Prognosen angewiesen, deren Qualität nur sehr schwer beurteilt werden kann. Soweit aber Sachverhalte quantifiziert werden können, ist es möglich, mit den quantitativen Prognosemethoden nachprüfbar zukünftige Beobachtungen zu prognostizieren. In der Unternehmensrechnung und im Controlling werden viele quantitative Größen ermittelt und dokumentiert, welche Grundlage für die Anwendung quantitativer Prognosemethoden sein können. Der Einsatz dieser Methoden erfordert, dass der Controller mit diesen Methoden vertraut ist, dass er die erforderlichen Eingabedaten ermitteln kann und dass eine geeignete Software auf einer Methodenbank zur Verfügung steht. Die sinnvolle Anwendung einer Methode erfordert es freilich auch, die rechnerischen Ergebnisse richtig zu interpretieren und die Grenzen dieser Methoden zu beachten. Es ist zu erwarten, dass die Leistung eines Controllers in der Zukunft sehr wesentlich auch daran gemessen wird, wie gut seine Prognosen sind.
Literatur:
Brockhoff, Klaus : Prognoseverfahren für die Unternehmensplanung, Wiesbaden 1977
Brockwell, Peter J./Davis, Richard A. : Time series: theory and methods, New York, 2. A., 1998
Hansmann, Karl-Werner : Kurzlehrbuch Prognoseverfahren, Wiesbaden 1983
Küpper, Willi/Lüder, Klaus/Streitferdt, Lothar : Netzplantechnik, Würzburg 1975
Schwarze, Jochen : Netzplantechnik: eine Einführung in das Projektmanagement, Herne, 7. A., 1994
Shumway, Robert H./Stoffer, David S. : Time series analysis and its applications, New York 2000
|