|
Clusteranalyse
Inhaltsübersicht
I. Grundlagen und Voraussetzungen
II. Modelle und Verfahren der Clusteranalyse
III. Anwendungsgesichtspunkte
I. Grundlagen und Voraussetzungen
1. Gegenstand und Zielsetzung
Die Clusteranalyse ist ein Teilgebiet der Datenanalyse und dient der Zusammenfassung von bestimmten Objekten zu Clustern, Klassen oder Gruppen, sodass zwischen Objekten derselben Klasse größtmögliche Ähnlichkeit und zwischen Objekten unterschiedlicher Klassen größtmögliche Verschiedenheit erreicht wird. Ausgangspunkt ist eine vorgegebene Menge N von Objekten; bei Fragestellungen des Marketing sind dies beispielsweise Konsumenten, Unternehmungen, Produkte, Regionen, Informationen etc. Die Objekte werden durch eine Auswahl M von Merkmalen beschrieben, die für jedes Objekt erhoben werden. Bezeichnet man die Ausprägung des Merkmals k ∊ M für das Objekt i ∊ N mit aik, so kann man diese Ausprägungen in einer Datenmatrix A übersichtlich anordnen. Für n Objekte und m Merkmale hat diese Matrix n Zeilen und m Spalten, man erhält die Darstellung
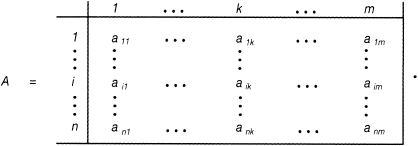
Unter einer Klassifikation der Objektmenge N versteht man nun allgemein eine Menge C = {C1, ?, Cs} von nicht leeren Objektteilmengen oder Klassen C1, ?, Cs, der Index s steht für die Klassenzahl.
Die Ermittlung einer Klassifikation erfolgt prinzipiell auf der Basis von Proximitätsmaßen, welche die Ähnlichkeiten oder Verschiedenheiten von Objekten oder Objektmengen bewerten und in der Regel aus den entsprechenden Zeilen der Datenmatrix zu berechnen sind. Objekte mit sehr ähnlichen Merkmalsausprägungen, also ähnlichen Zeilen, sollten derselben Klasse, Objekte mit sehr verschiedenen Merkmalsausprägungen verschiedenen Klassen angehören.
Vor Anwendung eines Klassifikations- oder Clusteranalyseverfahrens ist zu klären, welchen Klassifikationstyp man anstrebt. Man spricht von exhaustiver Klassifikation, wenn jedes Objekt mindestens einer Klasse zugeordnet wird, andernfalls von einer nicht exhaustiven Klassifikation. Sollen je zwei Klassen keine gemeinsamen Objekte enthalten, so heißt die Klassifikation disjunkt, andernfalls nichtdisjunkt. Ein disjunktes Klassifikationsergebnis bezeichnet man auch als Zerlegung oder Partition der Objektmenge, ein nichtdisjunktes Klassifikationsergebnis auch als Überdeckung oder Überlappung. Werden Klasen schrittweise durch Fusion oder Aufspaltung von Objektteilmengen gebildet, so spricht man von einer hierarchischen Klassifikation oder einer Hierarchie.
Je nach Klassifikationstyp werden die relevanten Verfahren zur Berechnung einer Klassifikation mit dem entsprechenden Attribut versehen. So wurde eine Vielzahl von Verfahren der partitionierenden und hierarchischen Clusteranalyse entwickelt. Sollen Überschneidungen zugelassen werden, so sind insbesondere Verfahren zur Bestimmung maximaler Cliquen in Betracht zu ziehen. Durch solche Verfahren wird in gewisser Weise das Problem angegangen, wie die zwischen sonst recht gut getrennten Klassen liegenden »Zwischenobjekte« zu erkennen und zu behandeln sind. Anstatt nun solche Objekte voll einer oder mehreren Klassen zuzuordnen, kann man alternativ für jedes Objekt i und jede Klasse Ci eine Zahl pij zwischen 0 und 1 einführen, die den Grad der Zugehörigkeit von i zu Ci quantifiziert. Dadurch kommt man zu so genannten unscharfen Klassifikationen, deren Berechnung mit Methoden der Fuzzy-Clusteranalyse erfolgt. Neuere Entwicklungen befassen sich mit Möglichkeiten, Clusteranalysen im Rahmen stochastischer Vorgaben durchzuführen. Man nimmt an, dass die Vektoren der Merkmalsausprägungen für die Objekte Zufallsvektoren sind und unterstellt für die Vektoren, die zu einer Klasse gehören, eine identische Verteilung. Derartige Ansätze werden in der probabilistischen Clusteranalyse behandelt.
2. Proximitätsmaße
Zur Beurteilung von Ähnlichkeiten oder Verschiedenheiten von zwei und mehreren Objekten oder Objektklassen verwendet man unterschiedliche Proximitätsmaße (Green, P. E./Tull, D. S. 1982). So bezeichnet man einen Index d(i,j), der die Verschiedenheit zweier Objekte i,j misst, als Distanzindex auf Objektpaaren. Man fordert d(i,i) = 0 für alle Objekte i und d(i,j) = d(j,i) ≥ 0 für je zwei verschiedene Objekte i,j (Bausch, T./Opitz, O 1993; Opitz, O. 1980). Die Eigenschaft »i und j sind ähnlicher als i^ und j^ wird durch d(i,j) < d(i^, j^) ausgedrückt.
Distanzindizes werden entweder direkt durch paarweisen Vergleich der Objekte erhoben, oder sie sind aus den Zeilen i und j der Datenmatrix je nach Datenniveau zu berechnen. Für mindestens intervallskalierte Merkmale ist
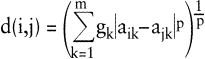
mit den merkmalspezifischen Gewichten
g1, ?,gm ≥ 0
ein sehr allgemeiner, sinnvoller Distanzindex. Für p = 1 ergibt sich die gewichtete City-Block-Distanz, für p = 2 die gewichtete euklidische Distanz. Für gk = 1 (k = 1, ?, m) erhält man ungewichtete Distanzindizes. Die City-Block-Distanz ist in gewisser Weise auf ordinale und nominale Daten übertragbar. Bei ordinalskalierten Merkmalen sind die Elemente entsprechender Datenmatrixspalten als Rangzahlen zu interpretieren. Der Index d(i,j) entspricht dann der Summe der (gewichteten) Rangdifferenzen der Objekte i,j. Fordert man bei nominalen Daten |aik – ajk| = 1 für aik ≠ ajk und |aik – ajk| = 0 für aik = ajk, so charakterisiert die City-Block-Distanz d(i,j) die (gewichtete) Anzahl der für die Objekte i,j verschiedenen Merkmalsausprägungen. Ist schließlich von einer Datenmatrix mit unterschiedlich skalierten Merkmalen auszugehen, so kann man Distanzindizes zunächst getrennt für nominal-, ordinal- oder intervallskalierte Merkmale ermitteln und diese zu einem aggregierten Gesamtindex addieren. Alternativ zu dem angegebenen Distanzkonzept ist es möglich, die Proximität von Objektpaaren durch Ähnlichkeitsindizes s(i,j) auszudrücken. Fordert man in diesem Fall 0 ≤ s(i,j) = s(j,i) ≤ s(i,i) = 1, so kann ein Zusammenhang von Distanz- und Ähnlichkeitskonzept etwa durch die Beziehung s(i,j) = 1 – d(i,j) hergestellt werden, nachdem d(i,j) auf das Intervall [0,1] normiert wurde.
Zur Bewertung der Verschiedenheit innerhalb von Klassen verwendet man einen Index h mit h(C) < h(C^), wenn die Klasse C homogener zusammengesetzt ist als C^.
Beispiele für h(C) sind
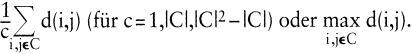
Die Verschiedenheit zwischen zwei Klassen wird durch einen Index v bewertet, wobei
v(C1,C2) < v(C^1, C^2) durch »C1, C2 sind ähnlicher als C^1,C^2« erklärt wird. Beispiele für v(C1,C2) sind die bei hierarchischen Clusteranalysen verwendeten Indizes
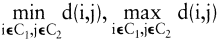
oder 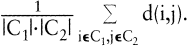 Zur Bewertung der Güte einer KlassifikationC benutzt man einen von C abhängigen Index b(C), beispielsweise Zur Bewertung der Güte einer KlassifikationC benutzt man einen von C abhängigen Index b(C), beispielsweise
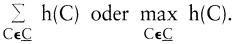
Für den Fall intervallskalierter Daten und
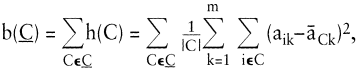
a¯Ck ist der Ausprägungsmittelwert des Merkmals k in Klasse C, erhält man das bekannte Varianzkriterium. Die Verschiedenheit h(C) innerhalb einer Klasse C wird dabei durch die Varianzsumme aller Merkmale in C beschrieben.
II. Modelle und Verfahren der Clusteranalyse
1. Partitionierende Clusteranalyse
Aufgabe der partitionierenden oder disjunkten Clusteranalyse ist die Bestimmung einer disjunkten Klassifikation oder PartitionC = {C1, ?, Cs} der Objektmenge N mit den Eigenschaften Ci ≠ Ø, Ci ⊂ N und Ci ∩ Cj = Ø für Ci, Cj ∊ C, wobei die Klassenzahl s vorgegeben ist (Opitz, O. 1980; Späth, H. 1983). Die Klassen enthalten paarweise keine gemeinsamen Objekte. Für N = {1,2,3,4,5} stellt beispielsweise C = {C1, C2} = {{1,2,3}, {4,5}} eine disjunkte Klassifikation mit zwei Klassen dar.
Bei gegebener Distanz d(i,j) geht man beispielsweise folgendermaßen vor:
| - | Wähle zufällig i1 ∊ N als Zentrum der Klasse C1. | | - | Wähle i2 ∊ N als Zentrum der Klasse C2, wenn d(i1,j) für j = i2 maximal wird. | | - | Für r = 3, ?,s wähle ir ∊ N als Zentrum der Klasse Cr, wenn min {d(i1,j), ?, d(ir – 1, j)} für j = ir maximal wird. | | - | Sind die Zentren i1, ?, is bestimmt, so ordne man die restlichen Objekte jeweils dem Zentrum mit minimaler Distanz zu. Man erhält für r = 1, ?, s |
Cr = {j ∊ N: min {d(i1,j), ?, d(i2,j)} = d(ir,j)}.
Die erhaltene Klassifikation C = {C1, ?, Cs} kann im Allgemeinen verbessert werden, wenn man weitere Verfahren anwendet. Dazu bezeichnet man das Ergebnis als Startklassifikation. Mit einem Austauschverfahren sucht man je nach vorgegebenem Bewertungsindex b(C) verbesserte Klassifikationen C 1, C 2, ? mit b(C) > b(C 1) > b(C 2) > ? nach folgender Vorschrift:
| - | Für alle Objekte i ∊ N wird geprüft, ob b(Cn) kleiner und damit besser wird, wenn i aus seiner Klasse in eine andere Klasse wechselt. | | - | Gegebenenfalls nehme man den Wechsel vor, der die maximale Abnahme von b(Cn) bewirkt, und erhält Cn+1 bzw. b(Cn+1). | | - | Man iteriere, bis keine weitere Verkleinerung von b mehr möglich ist. |
Das beschriebene Austauschverfahren liefert, wie viele Varianten dieser Methode, eine lokal optimale Zerlegung der Objektmenge.
Ist keine Startklassifikation der beschriebenen Art verfügbar, so kann man auch mit einer beliebig generierten disjunkten Klassifikation starten. Da aber in jedem Schritt nur ein Objekt die Klasse wechselt, führt dieses Verfahren relativ langsam zum Ziel. Um schnell in die Nähe einer günstigen Lösung zu gelangen, empfiehlt es sich, das Verfahren der Iterierten Minimaldistanzpartition anzuwenden. Dieses Verfahren basiert auf einem Bewertungsindex v({i},C) als Maß für die Distanz des Objekts i zur Klasse C. Ausgehend von C sucht man verbesserte Klassifikationen C 1, C 2, indem man für jedes Objekt i die Klasse C(i) wählt, die den Wert v({i},C) minimiert. Aus Cn entsteht Cn+1 durch
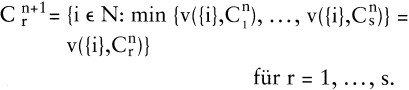
Dabei können mehrere Objekte die Klasse wechseln. Man erhält oft bereits nach wenigen Schritten die Identität Cn = Cn+1 und bricht das Verfahren ab.
Nachteilig ist jedoch zu vermerken, dass dieses Verfahren gelegentlich in einen Zyklus mündet, auch kann sich die Klassenzahl verringern. Ferner verzichtet man auf einen Index der Form b(C), der die Klassifikation insgesamt bewertet. Da eine Iterierte Minimaldistanzpartition jedoch im Allgemeinen zu rascheren Verbesserungen der Startklassifikation führt, empfiehlt es sich, dieses Verfahren zunächst auf C anzuwenden und anschließend ein Austauschverfahren zu nutzen.
Alle bisherigen Überlegungen zur Berechnung einer Partition basieren auf einer fest vorgegebenen Klassenzahl s. Andernfalls sind die beschriebenen Verfahren für mehrere s durchzuführen. Man betrachtet dann den Index b in Abhängigkeit von s und stellt die Wertepaare (s,b(s)) grafisch durch das so genannte Ellbogenkriterium dar. An der Stelle s* ergibt sich
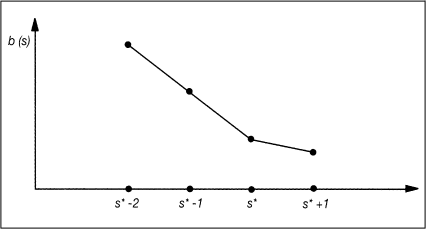
Abb. 1: Ellbogenkriterium
ein auffälliger Knick oder Ellbogen (vgl. Abb. 1). Bei weiterer Vergrößerung der Klassenzahl wird keine wesentliche Verkleinerung von b erreicht, sodass die Wahl von s* als Klassenzahl vernünftig erscheint.
Um die explizite Berechnung von Partitionen für verschiedene s zu umgehen, kann man s durch geeignete Klassenfusionen verkleinern oder durch Klassenaufspaltungen vergrößern. Das Vorgehen ist mithilfe der hierarchischen Clusteranalyse präzisierbar.
2. Hierarchische Clusteranalyse
Aufgabe der hierarchischen Clusteranalyse ist die Bestimmung einer hierarchischen Klassifikation oder HierarchieC mit den Eigenschaften Ci ≠ Ø, Ci ⊂ N sowie Ci ∩ Cj = Ø oder Ci ⊂ Cj oder Ci ⊃ Cj für Ci,Cj ∊ C. Betrachtet man zwei Klassen Ci, Cj, so besitzen die Klassen keine gemeinsamen Objekte, oder eine der Klassen ist in der anderen enthalten. Für N = {1,2,3,4,5} ist beispielsweise C = {{1}, {2}, {3}, {4}, {5}, {1,2}, {3,4}, {3,4,5}, N} eine hierarchische Klassifikation, die man mithilfe eines Dendrogramms übersichtlich darstellen kann (vgl. Abb. 2).
Zur Konstruktion von Hierarchien unterscheidet man divisive und agglomerative Verfahren (Bock, H. H. 1974; Opitz, O. 1980):
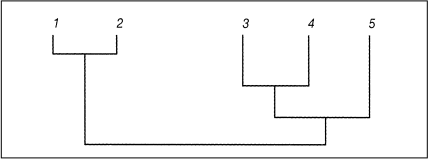
Abb. 2: Dendrogramm
Bei divisivem Vorgehen werden Klassen schrittweise aufgespalten. Ausgehend von der gesamten Objektmenge N ist der Aufspaltungsprozess so lange durchzuführen, bis sich einelementige Klassen ergeben. Für jede schrittweise erhaltene Partition C wird dabei eine Klasse C ∊ C gesucht, die sich »optimal« in zwei Teilklassen C1, C2 zerlegen lässt. Mithilfe eines Bewertungsindex der Form v soll dabei der Wert max {v(C1, C2): C1, C2 ⊂ C, C1 ∩ C2 = Ø}, für alle Klassen C ∊ C betrachtet, möglichst groß werden. Man erhält eine neue Partition mit einer Klasse mehr. Je nach Festlegung von v ergeben sich mehrere Verfahrensvarianten.
Die im Rahmen von divisiven Verfahren zu lösenden Optimierungsprobleme sind meistens sehr schwierig, der Rechenaufwand ist im Allgemeinen wesentlich höher als bei agglomerativen Verfahren, die darauf beruhen, Klassen schrittweise zusammenzufassen. Ausgehend von einelementigen Klassen ist der Fusionsprozess so lange durchzuführen, bis sich die gesamte Objektmenge als einzige Klasse ergibt. Für jede schrittweise erhaltene Partition C werden zwei Klassen Ci, Cj ∊ C gesucht, die optimal fusioniert werden können. Mithilfe eines Bewertungsindex der Form v ist dabei der Wert min {v (Ci, Cj): Ci, Cj ∊ C} zu ermitteln. Man erhält eine neue Partition mit einer Klasse weniger Um die sich ergebenden Partitionen mit abnehmender Klassenzahl im Vergleich bewerten zu können, benutzt man wieder das Ellbogenkriterium. Man betrachtet den Wert v der jeweils letzten Klassenfusion in Abhängigkeit der aktuellen Klassenzahl und stellt die Wertepaare (s,v) analog zu Abb. 1 dar. Offenbar ist ein entsprechendes Vorgehen auch bei divisiven Verfahren möglich.
Da nun eine Hierarchie als Folge von Partitionen mit zu- bzw. abnehmender Klassenzahl gesehen werden kann, scheint die hierarchische der partitionierenden Clusteranalyse überlegen zu sein. Andererseits ist festzustellen, dass ein Optimum nur für jede einzelne Aufspaltungs- bzw. Fusionsstufe erreicht werden kann, einmal erfolgte Aufspaltungen bzw. Fusionen sind nicht mehr korrigierbar.
Damit bietet sich eine Kombination von hierarchisch agglomerativen und Austauschverfahren an. Mithilfe eines hierarchischen Verfahrens und des Ellbogenkriteriums versucht man, zu einer günstigen Klassenzahl zu kommen, anschließend benutzt man die dazugehörige Partition als Startklassifikation für ein Austauschverfahren. Die Wiederholung des Vorgehens für benachbarte s-Werte erscheint plausibel.
Da agglomerative Verfahren aus Rechengründen divisiven Verfahren vorzuziehen sind, sollen hier die wesentlichen Varianten je nach Festlegung von v kurz vorgestellt werden.
Beim Single Linkage-Verfahren entspricht die Verschiedenheit von v (C, C ′) der Minimaldistanz zwischen den Klassen C, C ′. Dieses Verfahren neigt dazu, wenige umfangreiche Klassen zu bilden, andere Objekte bleiben isoliert. Andererseits kann man die Distanzen d beliebig monoton transformieren, ohne den Fusionsprozess zu verändern.
Beim Complete Linkage-Verfahren entspricht die Verschiedenheit v (C, C ′) der Maximaldistanz zwischen den Klassen C, C ′. Dieses Verfahren neigt dazu, Klassen gleichen Umfangs zu bilden. Auch in diesem Fall kann man die Distanzen d beliebig monoton transformieren, ohne den Fusionsprozess zu verändern.
Beide Verfahren eignen sich damit ohne jede Einschränkung für mindestens ordinale Distanzen, während die nachfolgenden Varianten streng genommen nur bei intervallskalierten Daten angewandt werden dürfen.
Beim Average Linkage-Verfahren entspricht die Verschiedenheit v (C, C ′) der Durchschnittsdistanz zwischen den Klassen C, C ′. Dieses Verfahren liegt bez. der Unterschiede in den Klassengrößen zwischen dem Single Linkage- und Complete Linkage-Verfahren und stellt damit in gewissem Sinn einen Kompromiss dar. Bezeichnet man im Fall intervallskalierter Daten mit a¯Ck bzw. a¯C ′k die mittleren Ausprägungen des Merkmals k in den Klassen C bzw. C ′, so entspricht die Verschiedenheit v (C, C ′) zwischen zwei Klassen C, C ′ beim Zentroid-Verfahren gerade dem quadrierten Abstand dieser Mittelwerte, aufsummiert über alle Merkmale.
Beim Ward-Verfahren multipliziert man schließlich den Index v des Zentroid-Verfahrens mit einem Faktor, der mit zunehmenden Klassengrößen wächst. Damit neigt das Ward-Verfahren, ähnlich wie Complete Linkage, jedoch in schwächerer Form, dazu, Klassen gleichen Umfangs zu bilden.
Trotz der gegebenen Hinweise auf Eigenschaften einzelner Verfahren fällt die Entscheidung für eine bestimmte Vorgehensweise in der Regel nicht leicht. Erfahrungsgemäß sind jedoch Complete Linkage- oder Ward-Ergebnisse leichter als andere zu interpretieren. Erzielt man andererseits mit unterschiedlichen Verfahren ähnliche Ergebnisse, so kann damit auf eine stabile und gut interpretierbare Klassenstruktur geschlossen werden.
Um das Gemeinsame bekannter agglomerativer Verfahrensvarianten zur Ermittlung einer Hierarchie herauszustellen, haben G.N. Lance und W.T. Williams eine Formel entwickelt, die die Verschiedenheit der nach erfolgter Fusion entstandenen neuen Klassen bewertet. Für zwei Klassen C, C ′ und C = C1 ∪ C2 gilt zunächst allgemein
v(C,C ′) = v(C1 ∪ C2,C ′)
= a1v(C1,C ′) + a2v(C2,C ′)
+ bv(C1,C2) + c|v(C1,C ′) – v(C2,C ′)|.
Danach hängt die Verschiedenheit v(C, C ′) der neu fusionierten Klasse C zu einer beliebigen anderen Klasse C ′ ab von der Verschiedenheit der Teilklassen C1 bzw. C2 zu C ′, der absoluten Differenz dieser beiden Verschiedenheiten und schließlich auch von der Verschiedenheit der beiden Teilklassen untereinander. Die folgende Tabelle zeigt, dass für die relevanten Verfahren die Lance/Williams-Formel bei spezieller Wahl der Parameter a1, a2, b, c mit a1, a2 > 0, a1 + a2 ≥ 1, b ≤ 0 erfüllt ist (vgl. Tab. 1).
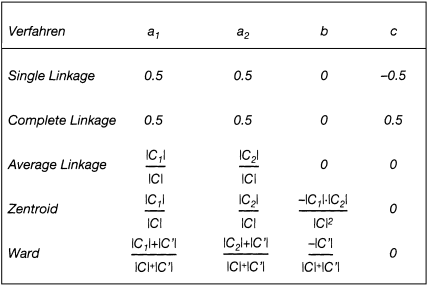
Tab. 1: Lance/Williams-Parameter für hierarchisch agglomerative Verfahren
3. Nichtdisjunkte Clusteranalyse
Aufgabe der nichtdisjunkten oder überlappenden Clusteranalyse ist die Bestimmung einer Klassifikation C = {C1, ?, Cs} der Objektmenge N mit den Eigenschaften Ci ≠ Ø, Ci ⊂N für Ci ∊ C. Die Klassen können sich überschneiden. Für N = {1,2,3,4,5} stellt beispielsweise C = {C1, C2} = {{1, 2, 3, 4}, {2, 4, 5}} eine nichtdisjunkte Klassifikation dar. Bei gegebener Distanz d(i,j) und einer Distanzschranke d ≥ 0 bezeichnet man die Teilmenge C ⊂ N als d^-Clique (Bock, H. H. 1974), wenn die Bedingung d(i,j) ≤ d^ für alle Objekte i,j ∊ C erfüllt ist. Die d^-Clique heißt maximal, wenn durch jedes Hinzufügen eines weiteren Objektes zu C die Bedingung verletzt wird. Im einfachsten Fall können maximale d^-Cliquen folgendermaßen konstruiert werden:
| - | Wähle ein Bezugsobjekt i ∊ N. | | - | Wähle i2 ∊ N mit d(i,i2) ≤ d^. | | - | Für r = 3,4, ? wähle ir mit d(i, ir),d(i2, ir), ?, d(ir – 1, ir) ≤ d^, bis kein weiteres Objekt mehr gefunden werden kann. Man erhält eine maximale Clique C(i) zum Bezugsobjekt i ∊ N. |
Das erhaltene Ergebnis ist jedoch nicht eindeutig, es hängt von der Reihenfolge der ausgewählten Objekte ab.
Variiert man die Distanzschranke d^ im Intervall [0, max d(i, j)], so entsteht eine Folge von maximalen Cliquen, die als Quasihierarchie (Bock, H. H. 1974; Opitz, O. 1980) interpretiert werden kann. Der Nachteil maximaler Cliquen mit wachsendem d^ besteht in der Konstruktion einer Vielzahl von Klassen mit unübersichtlichen Überschneidungen, dieser Effekt tritt offenbar kumuliert bei Quasihierarchien auf, weshalb derartige Konzepte für die Anwendung ungeeignet erscheinen.
Ein anderer Aspekt wird mit der Fuzzy-Clusteranalyse (Bock, H. H. 1979; Schader, M. 1981) verfolgt: Bei vorgegebener Klassenzahl s sind so genannte Zugehörigkeitsgrade pij der Objekte i ∊ N zu den Klassen ci mit pij ≥ 0 und pi1 + pi2 + ? pis = 1 zu bestimmen. Eine Fuzzy-Klassifikation wird dann beschrieben durch eine Matrix,
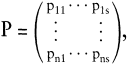
deren i-te Zeile die Zugehörigkeitsgrade des Objektes i ∊ N zu den Klassen enthält und deren j-te Spalte die Zugehörigkeitsgrade aller Objekte zur Klasse Ci angibt. Ein Objekt i heißt Kernobjekt der Klasse Cj für pij ≈ 1, Randobjekt von Cj für pij ≈ 0.
4. Anwendungssoftware
Die gängigen Verfahren partitionierender und hierarchischer Clusteranalyse auf der Basis von Daten- und Distanzmatrizen sind Bestandteil fast aller kommerzieller sowie auch frei verfügbarer Softwarepakete zur multivariaten Datenanalyse. Wichtige Vertreter kommerzieller Systeme sind beispielsweise SPSS, Clementine, SAS, S-PLUS, Systat, Statgraphics Centurion, matlab, Statistica oder PS-Explor/Statsys. Aus dem Bereich der nicht kommerziellen und frei verfügbaren Software sind ebenfalls eine Vielzahl von leistungsfähigen Systemen wie beispielsweise R, Weka, ViSta oder LispStat verfügbar. Speziellere Verfahren zur Fuzzy-Clusteranalyse und auf die Verarbeitung sehr großer Datenmatrizen zugeschnittene Algorithmen können bei einigen Systemen als Bibliothek zusätzlich eingebunden werden. Hervorzuheben ist in diesem Zusammenhang vor allem das System R, das über ein online verfügbares Archix (CRAN) von Erweiterungsbibliotheken den aktuellen Stand der Forschung im Bereich der Clusteranalyse gut abbildet.
III. Anwendungsgesichtspunkte
1. Interpretationshilfen für clusteranalytische Ergebnisse
Hat man eine Clusteranalyse durchgeführt und ein Klassifikationsergebnis der Form C = {C1, ?, Cs} erreicht, so stellt sich die Frage, wie die Klassen C1, ?, C2 untereinander abzugrenzen und durch welche Merkmalsausprägungen sie im Einzelnen zu beschreiben sind. Prinzipiell ist dazu die Datenmatrix heranzuziehen. Ist diese zu umfangreich, so empfiehlt es sich, für jede Klasse merkmalsspezifische Kennzahlen der Lage, z.B. Mittelwert, Median, Modus, sowie Kennzahlen der Streuung, z.B. Varianz, Spannweite, Quantilsabstände, Modalabweichung, zu berechnen (Bausch, T./Opitz, O. 1993). Durch den Vergleich derartiger Klassenkennzahlen wird die Beschreibung und Interpretation der Klassen in vielen Fällen erleichtert.
Eine andere Möglichkeit ist grundsätzlich durch die parallele Anwendung eines datenreduzierenden Verfahrens gegeben. Ist je nach Datenniveau mithilfe einer Faktorenanalyse oder Multidimensionalen Skalierung eine zweidimensionale grafische Repräsentation der Objekte möglich, die die Ähnlichkeiten bzw. Verschiedenheiten der Objekte angemessen wiedergibt, so kann damit das Klassifikationsergebnis zunächst visuell überprüft werden (Bausch, T./Opitz, O. 1993). Ferner können oft wichtige Merkmale als Vektoren in die grafische Darstellung so eingebettet werden, dass die Projektionen der Objekte auf diese Vektoren den Merkmalsausprägungen dieser Objekte gut entsprechen. Gegebenenfalls können damit die Objektpositionen inhaltlich beschrieben werden, ebenso auch ein Klassifikationsergebnis, falls die Klassen visuell gut getrennt sind (Gaul, W./Baier, D. 1993).
Die Dependenzanalyse verfolgt grundsätzlich das Ziel, ein oder mehrere abhängige Merkmale durch unabhängige Merkmale zu erklären (Green, P. E./Tull, D. S. 1982). Durch ein Klassifikationsergebnis C wird offenbar ein nominales Merkmal definiert, das von den übrigen bei der Clusteranalyse benutzten Merkmalen abhängt. Damit können je nach Datenniveau der unabhängigen Merkmale entsprechende Dependenzanalysen zur Klasseninterpretation angewandt werden. Sind die unabhängigen Merkmale mindestens intervallskaliert, so nutzt man die Diskriminanzanalyse, für nominalskalierte unabhängige Merkmale die Kontrastgruppenanalyse oder die Kategoriale Regression.
Neuere Ansätze der zweimodalen Clusteranalyse basieren auf der Idee, Objekte und Merkmale simultan zu klassifizieren (Furnas, G. W. 1980). Die dafür erforderliche Entwicklung von Distanzindizes auf Merkmalpaaren ist insofern problemlos, als das beschriebene Vorgehen zur Distanzbestimmung auf die transponierte Datenmatrix anwendbar ist. Die Ermittlung eines Distanzindex für Objekt-Merkmal-Paare erfordert jedoch mindestens ordinal interpretierbare Daten. Gegebenenfalls wählt man für den Distanzindex d(i,k) von Objekt i zu Merkmal k etwa die Differenz bzw. Rangdifferenz der maximal möglichen Ausprägung des Merkmals k und der erhobenen Ausprägung aik des Merkmals k für das Objekt i. Damit sind alle beschriebenen Clusteranalyseverfahren anwendbar. Die ermittelten Klassen enthalten nun i.a. nicht nur ähnliche Objekte, sondern auch ähnliche Merkmale sowie Merkmale mit hohen Ausprägungen für Objekte derselben Klasse. Eine Klasse, die nur Objekte enthält, ist bezüglich aller Merkmale eher niedrig ausgeprägt, eine reine Merkmalklasse deutet darüber hinaus an, dass die objektspezifische Verteilung der entsprechenden Merkmalsausprägungen relativ ähnlich ist.
2. Anwendungsrelevanz im Marketing
Gegenstand und Zielsetzung der Clusteranalyse zeigen sehr deutlich die Anwendungsvielfalt der diskutierten Modelle und Verfahren, z.B. in der Biologie, Medizin, Technik, Informatik, Linguistik, im Bibliothekswesen, in der Soziologie, Psychologie und Ökonomie, hier insbesondere im Marketingbereich (Backhaus, K. et al. 2003).
Offenbar liegt das Schwergewicht der Bedeutung von Clusteranalysen im Marketing in der Unterstützung von Problemen der Marktsegmentierung. Die Frage, heterogene Gesamtmärkte in möglichst homogene Teilmärkte aufzuspalten, weist direkt auf die Aufgabenstellung der Clusteranalyse hin. Auf der Nachfrageseite geht es dabei um die Aufdeckung von Käufergruppen ähnlichen Interessen, Bedarfs- und Kaufverhaltens, auf der Angebotsseite um die Analyse von Angebotsstrukturen, insbesondere um die Erkennung von Marktlücken und Marktverdichtungen. In diesem Fall entsprechen die Objekte konkurrierenden Produkten ähnlicher Beschaffenheit oder gleichen Verwendungszweckes oder auch ganzen Unternehmungen mit gut vergleichbaren Produktprogrammen.
Mit der Einrichtung von Testmärkten wird das Ziel verfolgt, die durch Einführung neuer Produkte und andere Marketingaktionen gewonnenen Erkenntnisse ohne wesentliche Verzerrungen auf den Gesamtmarkt hochzurechnen. Im Anticlustering versucht man, Klassen zu finden, sodass zwischen Objekten derselben Klasse größtmögliche Verschiedenheit erreicht wird. Eine einzelne Klasse könnte dann die Variabilität des Gesamtmarktes repräsentieren und auf diese Weise Hinweise auf interessierende Testmarkteinheiten liefern.
Weitere Anwendungsmöglichkeiten konzentrieren sich auch auf Bereiche der Marketing-Logistik. Ein Globalziel der Standortplanung ist die flächendeckende Versorgung eines Absatzgebietes. Die Positionierung von Auslieferungslagern, Verkaufsstellen etc. kann auch hier durch geeignete Ansätze des Anticlustering unterstützt werden. In der Tourenplanung geht es um die Frage, eine Menge von Bedarfsorten zeit- und kostenminimal zu bedienen. Die Zusammenstellung von Touren erweist sich als Problem der Reihenfolgeplanung, das mithilfe hierarchischer Clusteranalysen gut gelöst werden kann. Ein wesentlicher Gesichtspunkt der Mediaselektion ist die Erreichbarkeit potenzieller Nachfrager. Eine im Allgemeinen nichtdisjunkte Klassifikation dieser Nachfrager mit ihrem Mediennutzungsverhalten gibt oft Aufschluss über Erreichbarkeit und Nutzungsintensität und damit auch Hinweise auf eine effiziente Mediaselektionspolitik.
Stellt man Marktverhalten, Marktwirkung und zeitliche Absatzverläufe funktional dar, so erweist es sich oft als zweckmäßig, individuelle Zeitreihen und Wirkungsfunktionen clusteranalytisch zu aggregieren, um auf diese Weise Unterschiede in den wesentlichen Verhaltens- und Ursache-Wirkungsmustern aufzuspüren.
Insgesamt erscheint die Anwendung der Clusteranalyse immer dann nützlich, wenn es darum geht, Gruppierungen, Typologien, Datenzusammenhänge aufzudecken. Andererseits kann das Instrumentarium der Clusteranalyse stets nur als Hilfsmittel zur Lösung der behandelten Fragestellungen angesehen werden. Einerseits enthält jede Clusteranalyse eine Reihe von subjektiven Festlegungen wie Objekt- und Merkmalauswahl, Proximitätsmaße, Auswertungsverfahren, andererseits erfassen Modelle jeglicher Art immer nur Ausschnitte der Realität.
Literatur:
Backhaus, K./Erichson, B./Plinke, W. : Multivariate Analysemethoden, Berlin et al. 2003
Bausch, T./Opitz, O. : PC-gestützte Datenanalyse mit Fallstudien aus der Marktforschung, München 1993
Bock, H. H. : Automatische Klassifikation, Göttingen 1974
Bock, H. H. : Clusteranalyse mit unscharfen Partitionen, in: Studien zur Klassifikation, Bd. 6, hrsg. v. Bock, H. H., Frankfurt a.M. 1979, S. 137 – 163
Furnas, G. W. : Objects and their features: The metric represenation of two-class data, Stanford 1980
Gaul, W./Baier, D. : Marktforschung und Marketing Management, München et al. 1993
Green, P. E./Tull, D. S. : Methoden und Techniken der Marketingforschung, 4. A., Stuttgart 1982
Opitz, O. : Numerische Taxonomie in der Marktforschung, München 1978
Opitz, O. : Numerische Taxonomie, Stuttgart et al. 1980
Schader, M. : Scharfe und unscharfe Klassifikation qualitativer Daten, Königstein/Ts. 1981
Späth, H. : Cluster-Formation und -Analyse, München et al. 1983
|