|
Dienstleistungsproduktion
Inhaltsübersicht
I. Grundlegungen
II. Elemente und Struktur der Dienstleistungsproduktion
III. Produktionstheoretische Ansätze für Dienstleistungen
IV. Konsequenzen für die allgemeine Produktionstheorie
I. Grundlegungen
Der Dienstleistungsbegriff wird in der betriebswirtschaftlichen Literatur unterschiedlich abgegrenzt (vgl. Corsten, H. 1985; Engelhardt, W. H./Kleinaltenkamp, M./Reckenfelderbäumer, M. 1993; Hilke, W. 1989). Ohne auf diese Definitionsvorschläge einzugehen, werden im Folgenden Dienstleistungen als diejenigen Leistungen verstanden, die zu ihrer Erbringung einen externen Faktor (Nachfrager oder Objekt des Nachfragers) erfordern, d.h., dass ein Objekt aus dem Verfügungsbereich des Nachfragers in den Produktionsprozess des Anbieters eingebracht wird, um an diesem Faktor mit dem Ziel der Nutzenstiftung eine Transformation durchzuführen. Dienstleistungen sind damit spezifische Problemlösungen, die durch die Integration eines externen Faktors gekennzeichnet sind.
Der Begriff der Dienstleistungsproduktion hat sich zum heutigen Zeitpunkt noch nicht allgemein durchgesetzt. Geht man jedoch davon aus, dass Dienstleistungen produziert werden, dann ist es erforderlich, von einem rein technischen Produktionsverständnis abzurücken und einen erweiterten Produktionsbegriff einzuführen (Kern, W. 1976). Unter Produktion wird dann die sich in betrieblichen Systemen vollziehende Bildung von Faktorkombinationen im Sinne einer Anwendung technischer oder konzeptioneller Verfahren zur Transformation der dem Betrieb zur Verfügung stehenden originären und derivativen Produktionsfaktoren in absetzbare Leistungen oder in derivative Produktionsfaktoren, die dann in weiteren Faktorkombinationsprozessen genutzt oder in absetzbare Leistungen transformiert werden, zur Erfüllung des Sachziels unter Maßgabe der Formalzielerfüllung verstanden.
II. Elemente und Struktur der Dienstleistungsproduktion
Der Produktionsprozess lässt sich durch die Elemente Input, Throughput und Output abbilden. Input sind die Produktionsfaktoren. Hierunter sind Güter zu verstehen, die im Produktionsprozess kombiniert werden, um andere Güter hervorzubringen. In der betriebswirtschaftlichen Literatur existiert eine Vielzahl unterschiedlicher Faktorsysteme, wobei zwischen wirtschaftszweigabhängigen und wirtschaftszweigunabhängigen Systemen unterschieden werden kann (Corsten, H. 1985). Ein Aspekt, der in diesem Zusammenhang diskutiert wird, ist der externe Faktor, der auch als Objekt- oder Fremdfaktor bezeichnet wird. Hierunter ist ein Faktor zu verstehen, der vom Abnehmer einer Dienstleistung in den Produktionsprozess eingebracht wird und der sich somit der autonomen Disponierbarkeit durch den Produzenten entzieht (z.B. Patient, Kunde, Transportobjekt). Darüber hinaus ist darauf einzugehen, ob der Faktor Geld ein spezifischer Produktionsfaktor ist oder nicht. So lehnt Seng (Seng, P. 1989) die Behandlung monetärer Größen als Produktionsfaktor ab, weil er hierin einen Widerspruch zu dem in der Betriebswirtschaftslehre üblichen Vorgehen sieht, zwischen Nominalgüter- und Realgüterebene zu unterscheiden. Diese Vorgehensweise verkennt, dass dem monetären Faktor in einzelnen Dienstleistungszweigen (z.B. im Versicherungs- und Kreditwesen) eine andere Bedeutung zukommt als in Industrieunternehmungen (Deppe, H.-D. 1969; Farny, D. 1989; Haak, W. 1982; Mühlhaupt, L. 1977). In Versicherungen und Banken wird der monetäre Faktor zum eigentlichen Gegenstand des Leistungsprozesses, während er in industriellen Unternehmungen die Voraussetzung zur Beschaffung von Produktionsfaktoren darstellt. Der entscheidende Unterschied ist folglich darin zu sehen, dass der Faktor Geld in der industriellen Produktion nur mittelbar, und zwar über die Produktionsfaktorbeschaffung relevant wird, während er bei Versicherungen und Banken unmittelbar als Input in den Produktionsprozess einfließt. Darüber hinaus erfüllt der monetäre Faktor alle Merkmale eines Produktionsfaktors, d.h. er weist das Merkmal der Gutseigenschaft auf, er erfüllt die Funktion der causa efficiens für das Entstehen eines neuen Gutes, und sein Einsatz im Produktionsprozess ist mit einem Güterverzehr verbunden, wobei dieser in dem Verlust an Opportunitäten zu sehen ist (Corsten, H. 2001).
Der Throughput (Faktorkombination) stellt die Verbindung zwischen Input und Output her. In diesem Prozess werden Produktionsfaktoren auf der Grundlage eines entsprechenden Verfahrens mit dem Ziel kombiniert, die Inputfaktoren in die angestrebten Outputgüter zu transformieren. Dabei ist es in der Dienstleistungsliteratur üblich, die Faktorkombination in Vor- und Endkombination aufzuspalten. Der Vorkombination obliegt der Aufbau des Leistungspotenzials, d.h. sie befähigt die Unternehmung, im Rahmen der Endkombination entsprechend der unternehmerischen Sach- und Formalziele absetzbare Produkte herzustellen. Ergebnis der Vorkombination ist die Leistungsbereitschaft, d.h. das sofort verfügbare Leistungspotenzial. Aufgabe der Endkombination ist es dann, durch den Einsatz der Leistungsbereitschaft und weiterer interner Produktionsfaktoren unter Integration des externen Faktors absetzbare Leistungen zu erstellen, wobei die Produktion der Marktleistung in funktionaler Abhängigkeit von dem mengenmäßigen Einsatz des externen Faktors steht. Er ist damit eine grundlegende Voraussetzung für die Endkombination, d.h. sie ist nicht ohne zusätzliche, in der Unternehmung nicht vorhandene Produktionsfaktoren realisierbar.
Beim Output ist zwischen Vor- und Endkombination zu unterscheiden: Während sich der Output der Vorkombination auf die Fähigkeit bezieht, erwartete Nachfragen hinsichtlich bestimmter Cluster von beabsichtigten Änderungen an erwarteten externen Produktionsfaktoren erfüllen zu können, bilden die vorgenommenen Änderungen an den Eigenschaften des externen Faktors den Bezugspunkt des Output der Endkombination. Letzterer soll als Dienstleistungs-Output bezeichnet werden. Zusätzlich erlangt in der Output-Analyse die Dienstleistungsqualität eine besondere Bedeutung, weil sie sowohl durch anbieter- als auch nachfragerseitige Produktionsfaktoren determiniert wird.
Es ergibt sich dann die in Abb. 1 dargestellte grundsätzliche Struktur der Dienstleistungsproduktion (Altenburger, O. A. 1980; Corsten, H. 2001; Corsten, H./Gössinger, R. 2005).
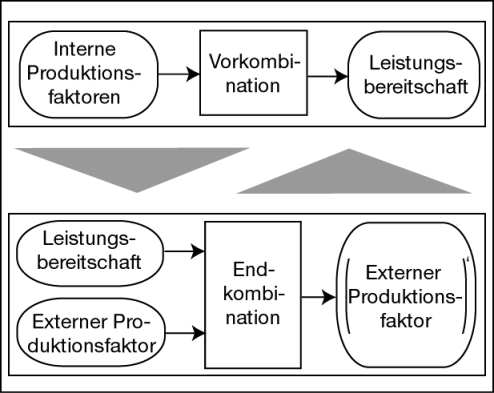
Abb. 1: Grundmodell der Dienstleistungsproduktion
III. Produktionstheoretische Ansätze für Dienstleistungen
In der Literatur existieren unterschiedliche Ansätze zur produktionstheoretischen Modellierung von Dienstleistungen (vgl. Abb. 2). Im Folgenden seien zunächst beispielhaft zwei spezielle Ansätze vorgestellt, bevor dann ein Ansatz für eine allgemeine produktionstheoretische Modellierung skizziert werden soll.
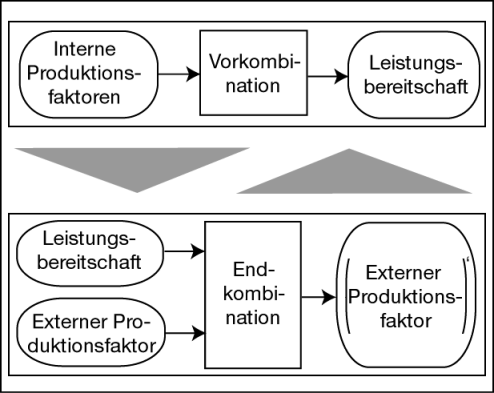
Abb. 2: Produktionstheoretische Ansätze für Dienstleistungen im Überblick
1. Beispiele für spezielle Ansätze a) Produktionsfunktion für Versicherungsunternehmungen als institutionenbezogener Ansatz
Die produktionstheoretische Durchdringung von Versicherungen ist eng mit den Arbeiten von Eisen (Eisen, R. 1971) und Farny (Farny, D. 1965; Farny, D. 1989) verknüpft. Dabei wird das Risiko- und Dienstleistungsgeschäft ins Zentrum der Überlegungen gerückt, weil die Bereiche Kapitalanlage und sonstige Geschäfte nicht versicherungsspezifisch sind. Ausgangspunkt ist die Gesamtproduktionsfunktion
PFi = fij (Pj)
mit
PFi = Produktionsfaktormengen (i = 1, ?,r);
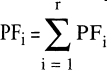 (als Kurzschreibweise) (als Kurzschreibweise)
Pj = Versicherungsprodukte (j = 1, ?,s);
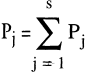 (als Kurzschreibweise), (als Kurzschreibweise),
die dann in eine Produktionsfunktion für das Risiko- und eine für das Dienstleistungsgeschäft zerlegt wird. Für das Risikogeschäft gilt:
RTk = fjk(Pj),
d.h. es besteht eine funktionale Beziehung zwischen den Versicherungsprodukten (Pj) und den darin enthaltenen Risikotransfers (RTk), wobei die Gesamtheit RTk das Kollektiv der versicherten Risiken abbildet. Da für die Gewährung des Versicherungsschutzes der Einsatz von Produktionsfaktoren notwendig ist, d.h.
PFi = fik(RTk)
ergibt sich für das Risikogeschäft die folgende Produktionsfunktion:
PFi = fik[fkj(Pj)]
Das Dienstleistungsgeschäft ist ein äußerst komplexes System von Input-Output-Beziehungen, wobei die in Tabelle 1 erfassten Elemente zu unterscheiden sind:

Tab. 1: Elemente des Dienstleistungsgeschäfts
Da externe Leistungen teilweise durch originäre Produktionsfaktoren erstellt werden (z.B. freie Sachverständige), gilt:
PFi = fil(eLl),
sodass sich die folgende Produktionsfunktion ergibt:
PFi = fil[flj(Pj)]
Auch bei den externen Leistungen mit vorgelagerten produktbezogenen Leistungen ist der Einsatz von Produktionsfaktoren erforderlich
PFi = fim(piLm),
sodass sich die folgende Funktion ergibt:
PFi = fim〈fml[flj(Pj)]〉
Für externe Leistungen mit vorgelagerten nicht produktbezogenen innerbetrieblichen Leistungen gilt dann:
PFi = fin(npiLn)
und
PFi = fin〈fnl[flj(Pj)]〉
Sind für die externen Leistungen produktbezogene innerbetriebliche Leistungen erforderlich, die nicht produktbezogene innerbetriebliche Leistungen voraussetzen, dann gilt:
piLm = fml(eLl) und
npiLn = fnm(piLm)
Da auch die nicht produktbezogenen innerbetrieblichen Leistungen den Einsatz von Produktionsfaktoren erfordern
PFi = fin(npiLn),
ergibt sich als Produktionsfunktion:
PFi = fin{fnm〈fml[flj(Pj)]〉}
Die Zusammenfassung dieser Teilfunktionen ergibt dann die Produktionsfunktion für das gesamte Dienstleistungsgeschäft:
PFi = fil[flj(Pj)] + fim〈fml[flj(Pj)]〉 + fin〈fnl[flj(Pj)]〉 + fin{fnm〈fml[flj(Pj)]〉}
Diese Beziehung gibt den Faktorverbrauch für alle im Rahmen des Dienstleistungsgeschäftes zum Einsatz gelangenden Produktionsfaktoren wieder. Die Gesamtproduktionsfunktion ergibt sich dann durch die Aggregation der Teilfunktionen für das Risiko- und Dienstleistungsgeschäft. b) Technologie für Logistikleistungen als funktionenbezogener Ansatz
Die Logistikleistung konkretisiert sich an dem logistischen Objekt (z.B. Personen, Sachobjekte, Informationen) als Transformation, d.h. einer Veränderung der temporalen und/oder lokalen Eigenschaften. Neben Transport und Lagerung, die diese Veränderung originär bewirken, sind für die logistische Leistungserstellung Leistungsarten wie etwa Umschlag und Bündelung relevant, die eine Veränderung von Zuordnungseigenschaften herbeiführen. Die bei der Erbringung dieser Teilleistungen gleichzeitig angestrebte Aufrechterhaltung der Quantität und substantiellen Beschaffenheit logistischer Objekte lässt sich jedoch mit einer rein mengenorientierten Erfassung der Logistikleistung nicht adäquat abbilden. Zur differenzierten Modellierung dieses Sachverhalts ist es erforderlich, den Zustand des logistischen Objekts mit Hilfe von Eigenschaften zu erfassen (vgl. Isermann, H. 1999). Aus der Perspektive der logistischen Leistungserstellung wird der Zustand eines Objekts zeitpunktbezogen durch Angaben
| - | zum Ort (z.B. geographische Koordinaten), | | - | zur qualitativen Beschaffenheit (z.B. Unversehrtheit, Temperatur), | | - | zur Zuordnung des Objekts zu Lagerplätzen und Transportmitteln und | | - | zur Zugehörigkeit zu übergeordneten logistischen Objekten |
beschrieben. Aufgrund dieser logistikspezifischen Auswahl von Eigenschaften wird der erfasste Zustand als logistischer Zustand zt bezeichnet, der einen Teil des allgemeinen Objektzustands darstellt. Bei M logistikrelevanten Eigenschaften zm.t (m = 1, ?, M) des Objekts lautet der Vektor des logistischen Zustands:
zt = (z1.t ? zM.t)T
Durch einen logistischen Leistungserstellungsprozess P, der zum Zeitpunkt t = a beginnt und zum Zeitpunkt t = e endet, wird der Anfangszustand des Objekts za in einen Endzustand ze transformiert:
P: za→ze
Ein logistischer Leistungserstellungsprozess besteht in der Regel nicht aus einer einzelnen Aktivität, sondern ergibt sich aus einer Folge von Teilprozessen unterschiedlicher Art:
| - | Vorgelagerte sekundäre Elementarkombinationen PkV stellen aus dem generellen Leistungspotential des Logistiksystems durch Auswahl und Verfügbarmachung interner Produktionsfaktoren eine Leistungsbereitschaft für konkret vorliegende Leistungsobjekte her, die die Ausführung von primären Elementarkombinationen ermöglicht. | | - | Primäre Elementarkombinationen PkH beziehen sich auf logistische Objekte, d.h., ihre Ausführung geht unmittelbar mit sachzielbezogenen Transformationen der Zustände logistischer Objekte einher. | | - | Nachgelagerte sekundäre Elementarkombinationen PkN heben nach der Ausführung der primären Elementarkombination die dafür geschaffene Leistungsbereitschaft wieder auf, um die involvierten internen Produktionsfaktoren für andere primäre Elementarkombinationen nutzbar zu machen. |
Ein k-stufiger logistischer Leistungserstellungsprozess (k = 1, ?, K) mit den Teilprozessen PkV, PkH und PkN ist durch eine Folge von Zuständen des logistischen Objekts gekennzeichnet:
{za = za.1, ze.1, ?, za.K, ze.K = ze}
Die Zustandsänderung za→ze ist genau dann ein vereinbarungskonformer Output des Leistungserstellungsprozesses, wenn der Endzustand ze der mit dem Nachfrager getroffenen Leistungsvereinbarung entspricht. Die Menge ZeV umfasst dabei alle alternativ möglichen, vereinbarungskonformen Endzustände:
ze ∊ ZeV
Die neben dem logistischen Objekt für die Leistungserstellung relevanten N Güterarten werden durch Mengen xn.t.k (n ∊ N, N = {1, ?, N}) abgebildet. Der Netto-Güterfluss wn.kH der primären Elementarkombination k, die mit der Zustandsänderung za.k→ze.k am logistischen Objekt einhergeht, ergibt sich aus der Gegenüberstellung des Güterbestands vor xn.a.kH und nach xn.e.kH der Teilprozessausführung. Der Flussvektor der primären Elementarkombination k lautet:
wkH = (w1.kH ? wN.kH)T mit wn.kH = xn.a.kH – xn.e.kH
Der Netto-Güterfluss einer Stufe des logistischen Leistungserstellungsprozesses ergibt sich dabei durch Addition der entsprechenden Teilprozess-Netto-Güterflüsse:
wk = wkV + wkH + wkN
Eine mit dem Nachfrager getroffene Leistungsvereinbarung kann durch R unterschiedliche logistische Leistungserstellungsprozesse erfüllt werden. Jeder logistische Leistungserstellungsprozess ist dabei durch eine spezifische Anzahl von Wiederholungen der Teilprozesse (Prozessmengen) auf den einzelnen Stufen gekennzeichnet, die durch Vektoren gr abgebildet werden. Der Netto-Güterfluss wr eines Leistungserstellungsprozesses ergibt sich damit aus:
wr = (w1.r ? wN.r) mit wn.r = w n.1.r g1.r + ? + wn.K.r gK.r
2. Eigenschaftsorientierte Korrespondenzen als Beispiel für einen allgemeinen Ansatz
Eine Durchsicht der in der Literatur vorgestellten Modellierungen zur Dienstleistungsproduktion lässt die folgenden Aussagen zu:
| - | Der formalen Spezifikation des Output kommt eine eher untergeordnete Bedeutung zu. | | - | Der externe Produktionsfaktor wird zwar in seiner Bedeutung einheitlich hervorgehoben, jedoch zeigt seine formale Erfassung eher rudimentäre Züge. | | - | Die Interaktion zwischen Nachfrager und Anbieter und/oder deren Wirkung im Rahmen der Endkombination wird nur selten in die Modellierung aufgenommen. |
Vor diesem Hintergrund gibt es aktuelle Entwicklungen, die einen produktionstheoretischen Modellentwurf für Dienstleistungen vorstellen, der zur Erfassung der Güter auf Eigenschaften (vgl. Corsten, H./Gössinger, R. 2003; Corsten, H./Gössinger, R. 2006) und zur Abbildung der Produktionsprozesse auf die stochastische Netzplantechnik zurückgreift (vgl. Corsten, H./Gössinger, R. 2004a; Corsten, H./Gössinger, R. 2005; Gössinger, R. 2005). Wesentliche Elemente dieses Ansatzes sind dabei:
| - | Dienstleistungen werden als Problemlösungen (vgl. Kern, W. 1979) aufgefasst, wobei diese in einem veränderten Ist-Zustand des Betrachtungsobjektes und/oder einer veränderten Vorstellung des Wirtschaftssubjektes über den Soll-Zustand zu sehen sind. | | - | Um die gewünschten Eigenschaftsänderungen am externen Produktionsfaktor (Output-Eigenschaftsänderungen) herbeizuführen, müssen Eigenschaftsänderungen an internen Produktionsfaktoren (Input-Eigenschaftsänderungen) hingenommen werden (z.B. zeitliche Nichtverfügbarkeit zur Erbringung anderer Dienstleistungen). Dieser Zusammenhang lässt sich durch Rückgriff auf das Konstrukt „ Aktionensystem “ herstellen, das die zur Erbringung einer Dienstleistung erforderlichen Aktionen und deren Beziehungen zueinander erfasst: | | - | Da bei Dienstleistungen häufig beidseitig mehrdeutige Beziehungen zwischen den Input- und Output-Eigenschaftsänderungen auftreten, wird zur Modellierung von Aktionen auf eigenschaftsbezogene Korrespondenzen zurückgegriffen. | | - | Aufgrund der Interaktionen im Dienstleistungserstellungsprozess können die Beziehungen zwischen den Aktionen mehrdeutig sein. Dies zeigt sich etwa darin, dass den Entscheidungsträgern mehrere Möglichkeiten zur Fortsetzung des Transformationsprozesses offenstehen. Zur Abbildung dieser Beziehungen eignet sich die stochastische Netzplantechnik in der Form der Graphical Evaluation and Review Technique (GERT). |
IV. Konsequenzen für die allgemeine Produktionstheorie
Die verallgemeinerte produktionstheoretische Betrachtung sprengt jedoch den Rahmen der traditionellen produktionstheoretischen Modellierung, in der Produktionsprozesse bezüglich ihrer technischen und/oder naturgesetzlich determinierten Wirkungen auf Transformationsobjekte analysiert und auf der Grundlage von Input- und Output-Gütermengenänderungen erfasst werden (vgl. Dyckhoff, H. 1994). Es ergibt sich damit die Notwendigkeit einer Erweiterung der traditionellen Produktionstheorie, da in dieser Betrachtungsweise
| - | die Produktion weitgehend unabhängig von ihren Beziehungen zu ihrer Umwelt analysiert wird, | | - | die Qualität der involvierten Güter lediglich implizit über unterschiedliche Güterarten erfasst werden kann und | | - | ein idealisiertes Entscheidungsverhalten unterstellt wird. |
Erste Erweiterungsvorschläge wurden vor dem Hintergrund des Schutzes der ökologischen Umwelt in die produktionstheoretische Analyse eingebracht (vgl. Dyckhoff, H. 2003). Neben der Erfassung umweltrelevanter Eigenschaften der Inputs und Outputs (vgl. Houtman, J. 1998) ist die Berücksichtigung eines mehrdimensionalen und multipersonalen Präferenzkonstruktes zu nennen (vgl. Behrens, S. 1999). Bei der Dienstleistungsproduktion ergibt sich das Erfordernis der Erweiterung aus der Integrativität, da sich hieraus für den Nachfrager die Möglichkeit ergibt, den Dienstleistungserstellungsprozess wahrzunehmen und zu beurteilen und er als „ Koproduzent “ an der Erstellung beteiligt ist, wobei sich die Wahrnehmungen und Beurteilungen in seinen Handlungen niederschlagen. Neben den Produzenten sind damit weitere Subjekte, die den Produktionsprozess beeinflussen, zu berücksichtigen. In der Abbildung 3 wird ein erweiterter produktionstheoretischer Rahmen vorgestellt (vgl. Corsten, H./Gössinger, R. 2004b).
Dabei wird die Grundaussage der Produktionstheorie, dass eine Produktion durch Gütereinsatz und -ausbringung Änderungen von Güterknappheiten in der Unternehmung bewirkt, in zwei Aspekten verallgemeinert:
| - | Nicht nur Gütermengen-, sondern auch Eigenschaftsänderungen können den Input und den Output bilden. | | - | Die bewirkten Änderungen können in der Unternehmung und darüber hinaus in einer allgemein definierten Umwelt ihren Niederschlag finden. |
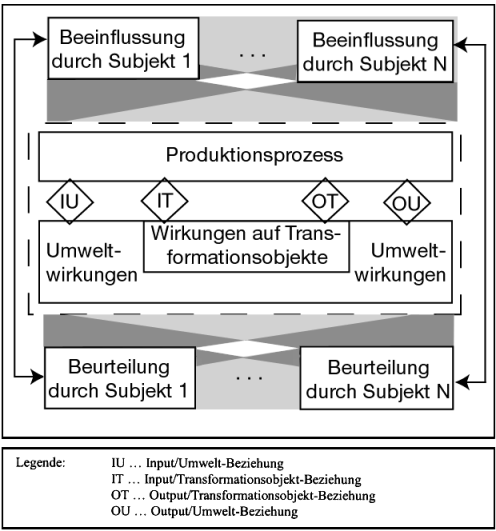
Abb. 3: Entwurf eines erweiterten produktionstheoretischen Rahmens
Ferner wird die Annahme der ausschließlichen Beeinflussung der Produktion durch einen vollständig rational handelnden Produzenten aufgelöst und unterstellt, dass mehrere beschränkt rational handelnde Subjekte einen Einfluss auf die Produktion ausüben können, der direkter oder indirekter Natur sein kann:
| - | Die direkt produktionsbeeinflussenden Handlungen der Subjekte sind dabei von ihrem Entscheidungsverhalten abhängig, dem aufgrund der Subjektivität der Wahrnehmung der Produktion und der Präferenzen unterschiedliche Beurteilungen der Produktion zugrunde liegen können. | | - | Ein indirekter Einfluss auf die Produktion gründet auf der Wahrnehmung und Beurteilung beteiligter Subjekte durch andere beteiligte Subjekte und einer darauf aufbauenden Subjektbeeinflussung (z.B. durch Interaktion), die eine Produktionsbeeinflussung zur Folge hat. |
Literatur:
Altenburger, O. A. : Ansätze zu einer Produktions- und Kostentheorie der Dienstleistungen, Berlin 1980
Behrens, S. : Grundlagen der prozeßorientierten Produktionstheorie, in: Die Theorie der Unternehmung in Forschung und Praxis, hrsg. v. Albach, H. et al., Berlin et al. 1999, S. 297 – 312
Corsten, H. : Die Produktion von Dienstleistungen, Berlin 1985
Corsten, H. : Dienstleistungsmanagement, 4. A., München et al. 2001
Corsten, H./Gössinger, R. : Rahmenkonzept zur integrativen Modellierung von Dienstleistungen, Schriften zum Produktionsmanagement Nr. 58, Kaiserslautern 2003
Corsten, H./Gössinger, R. : Modellierung von Dienstleistungen. Perspektiven einer integrativen Vorgehensweise, in: Forum Dienstleistungsmanagement. Dienstleistungsinnovationen, hrsg. v. Bruhn, M./Stauss, B., Wiesbaden 2004a, S. 127 – 148
Corsten, H./Gössinger, R. : Überlegungen zur Produktionstheorie – Zugleich Stellungnahme und Ergänzung zu dem Beitrag „ Neukonzeption der Produktionstheorie “ von Harald Dyckhoff in der ZfB, 73. Jg. (2003), S. 705 – 732, in: ZfB, 2004b, S. 511 – 522
Corsten, H./Gössinger, R. : Entwurf eines produktionstheoretischen Rahmens für Dienstleistungen, in: Dienstleistungsökonomie. Beiträge zu einer theoretischen Fundierung, hrsg. v. Corsten, H./Gössinger, R., Berlin 2005, S. 153 – 188
Corsten, H./Gössinger, R. : Output-Flexibilität in der Dienstleistungsproduktion – Eine produktionstheoretische Analyse, in: ZfB, 2006, S. 29 – 53
Deppe, H.-D. : Bankbetriebliches Wachstum, Stuttgart 1969
Dyckhoff, H. : Betriebliche Produktion. Theoretische Grundlagen einer umweltorientierten Produktionswirtschaft, 2. A., Berlin et al. 1994
Dyckhoff, H. : Neukonzeption der Produktionstheorie, in: ZfB, 2003, S. 705 – 732
Eisen, R. : Zur Produktionsfunktion der Versicherung, in: ZVersWiss., 1971, S. 407 – 419
Engehardt, W. H./Kleinaltenkamp, M./Reckenfelderbäumer, M. : Leistungsbündel als Absatzobjekte, in: ZfbF, 1993, S. 395 – 426
Farny, D. : Produktions- und Kostentheorie der Versicherung, Karlsruhe 1965
Farny, D. : Versicherungsbetriebslehre, Karlsruhe 1989
Gössinger, R. : Dienstleistungen als Problemlösungen. Eine produktionstheoretische Analyse auf der Grundlage von Eigenschaften, Wiesbaden 2005
Haak, W. : Produktion in Banken, Frankfurt a.M. et al. 1982
Hilke, W. : Grundprobleme und Entwicklungstendenzen des Dienstleistungs-Marketing, in: Dienstleistungs-Marketing, hrsg. v. Hilke, W., Wiesbaden 1989, S. 5 – 44
Houtman, J. : Elemente einer umweltorientierten Produktionstheorie, Wiesbaden 1998
Isermann, H. : Produktionstheoretische Fundierung logistischer Prozesse, in: Planung und Steuerung von Input-Output-Systemen, ZfB-Ergänzungsheft 4/99, hrsg. v. Albach, H./Rosenberg, O., Wiesbaden 1999, S. 67 – 87
Kern, W. : Die Produktionswirtschaft als Erkenntnisbereich der Betriebswirtschaftslehre, in: ZfbF, 1976, S. 756 – 767
Kern, W. : Produkte, Problemlösungen als, in: HWProd, hrsg. v. Kern, W., Stuttgart 1979, Sp. 1563 – 1572
Mühlhaupt, L. : Einführung in die Betriebswirtschaftslehre der Banken, Wiesbaden 1977
Schröder, H.-H. : Zum Problem einer Produktionsfunktion für Forschung und Entwicklung, Meisenheim am Glan 1973
Seng, P. : Informationen und Versicherungen, Wiesbaden 1989
|