|
Hedging
Inhaltsübersicht
I. Grundbegriffe und Systematisierung des Hedging
II. Arten und Motive des Hedging
III. Hedging als Teil des Risikomanagements
I. Grundbegriffe und Systematisierung des Hedging
1. Grundbegriffe des Hedging
Im Sprachgebrauch des Risikomanagements versteht man unter Hedging die Risikoreduktion oder vollständige Risikoeliminierung einer offenen Position (Grundgeschäft), z.B. einer Kassaposition in Wertpapieren. Das Risiko wird dabei als Höhe des Verlustes aufgrund von Preisänderungen aufgefasst (Steiner, M./Meyer, F. 1993). Das Collins Dictionary erklärt das Verb hedge als: „ to protect against loss through future price fluctuations as by investing in futures “ .
Weiter gefasst lassen sich nach Ederington drei Zielsetzungen des Hedging unterscheiden (Ederington, L .H. 1979):
Die gewünschte Risikoreduzierung bzw. Risikoeliminierung könnte am einfachsten dadurch erfolgen, dass die betroffene Position zum aktuellen Marktpreis P verkauft und der Erlös risikolos investiert wird. Beim Hedging geht man jedoch davon aus, dass das Grundgeschäft aufrechterhalten bleiben soll und durch ein geeignetes Gegengeschäft F (Sicherungsgeschäft) eine negative Preisentwicklung der Gesamtposition aus beiden Geschäften vermieden oder verringert werden soll.
Hedging zum Erzielen von Basisgewinnen wird hingegen durchgeführt, wenn der Hedger damit rechnet, dass sich die Basis B als Differenz aus Terminkurs F und Kassapreis P des zu hedgenden Instruments ändert. Dies ist möglich, wenn die Größen F und P nicht vollständig korreliert sind.
In Anlehnung an die Portfolio Selection spricht man von Portfolio Hedging, wenn das Risiko eines Portfolios durch optimale Kombination von Kassa- und Terminpositionen minimiert werden soll. Dabei wird unterstellt, dass die Marktteilnehmer für ihre Hedgingentscheidungen die erwartete Rendite und das erwartete Risiko in Form der Varianz bzw. Standardabweichung der Renditen verwenden. Eine risikominimale Kombination von Kassa- und Terminposition ist als optimale Hedge Ratio h* gegeben, wenn das gewählte Verhältnis von zu verkaufenden Terminkontrakten zu Kassainstrumenten die Varianz der Portfoliorendite minimiert. Die Hedge Ratio h wird entweder analytisch oder über lineare Einfachregression aus den historischen Renditen des Kassa- und Termininstruments bestimmt (Ederington, L .H. 1979). In diesem Fall entspricht die risikominimale Hedge Ratio dem negativen Regressionskoeffizienten, d.h. h* = – β. Das negative Vorzeichen gibt an, dass eine gegenläufige Position eingegangen wird.
2. Systematisierung des Hedging a) Cash Hedge und Anticipatory Hedge
Das Grundgeschäft ist üblicherweise eine Kassaposition, während als Gegengeschäft ein Termingeschäft (Forwardkontrakt) oder ein Optionskontrakt angenommen wird. Dieser Fall wird als Cash Hedge bezeichnet. Allerdings können durch Hedging auch Risiken reduziert werden, indem Terminkontrakte als temporärer Ersatz für später ohnehin fällige Verträge abgeschlossen werden (Spremann, K. 1986). Damit werden die Risiken aus zukünftig erforderlichen Kassageschäften ebenfalls reduziert oder eliminiert; Beispiele sind etwa die Unsicherheit über künftige Erzeugungsmengen oder Verkaufspreise, die Wechselkursschwankungen bei Exportgeschäften oder Zinsschwankungen bei der Emission festverzinslicher Titel. Man spricht in diesem Fall von einem Anticipatory Hedge. b) Long Hedge und Short Hedge
In beiden vorgenannten Fällen kann danach unterschieden werden, ob das Grundgeschäft eine Bestandsposition (long position) oder eine Verpflichtung (short position) darstellt. Üblicherweise handelt es sich beim Cash Hedge um die Absicherung einer Bestandsposition, der eine short position, also ein Verkauf von Terminkontrakten gegenübergestellt werden muss. Man bezeichnet dies als einen Short Hedge. Ist das Grundgeschäft jedoch eine Verpflichtung, z.B. zur Zahlung eines gegebenen Betrages in Fremdwährung, so kann dieses durch einen Long Hedge, z.B. den Kauf einer entsprechenden Anzahl (long position) von Forward-Kontrakten abgesichert werden. c) Mikro Hedge und Makro Hedge
Ein Mikro Hedge liegt vor, wenn für jede Position aus Grundgeschäften (z.B. Bestandspositionen eines Handelsbuches) eine gegenläufige Hedge Position aufgebaut wird. Die Aufrechnung von bereits bestehenden long und short Positionen in den Grundgeschäften unterbleibt hierbei. Beim Makro Hedge werden zunächst die einander in Art und Laufzeit entsprechenden long und short Positionen gegeneinander gestellt (netting) und lediglich der jeweilige Überhang abgesichert. d) Pure Hedge und Cross Hedge
Damit sich die Preisentwicklung des Grund- und Absicherungsgeschäfts möglichst ausgleichen, ist eine hohe Korrelation beider Geschäfte vorteilhaft. Das benötigte negative Vorzeichen der Korrelation kann durch eine entsprechende Gestaltung der Absicherungsposition (long oder short) erzeugt werden. Ein Pure Hedge ist gegeben, wenn das Grundgeschäft und das Underlying des Termingeschäfts in der Art übereinstimmen (z.B. DAX-Portfolio und DAX-Futures Kontrakt an der EUREX) oder Kassa- und Terminpositionen im Devisenhandel und somit eine hohe Korrelation zwischen Kassapreis P und Forward-/Futurespreis F vorliegt. Die Basis B = F – P verläuft damit nahezu deterministisch, d.h. ein Basisrisiko existiert kaum.
Da häufig das Grundgeschäft nicht mit einem übereinstimmenden Termingeschäft abgesichert werden kann (z.B. Portfolios in einer Zusammensetzung, die nicht dem DAX entspricht), muss auf Gegengeschäfte ausgewichen werden, die in wesentlichen Merkmalen abweichen, deren Preise sich aber dennoch möglichst gleichlaufend entwickeln (Cross Hedge). Das Risiko einer negativen Preisentwicklung P wird somit durch ein nicht mehr geringes Basisrisiko B = F – P eingetauscht. Bei positiver Korrelation zwischen F und P wird das Gesamtrisiko jedoch auf jeden Fall verringert. e) Statischer Hedge und Dynamischer Hedge
Bezüglich des Zeitpunkts zu dem das Grundgeschäft abgesichert werden soll, unterscheidet man danach, ob dieser Zeitpunkt fest gegeben ist (Statischer Hedge, Starker Hedge), oder ob während einer vorgegebenen Haltedauer eine Risikoabsicherung gegeben sein soll (Dynamischer Hedge, Schwacher Hedge). Im zuerst genannten Fall wird die Laufzeit des Gegengeschäfts möglichst exakt an den gewünschten Absicherungszeitpunkt T angepasst. Beim theoretischen Fall des Dynamischen Hedges wird zu jedem denkbaren Zeitpunkt während einer Haltedauer der Hedge risikooptimal angepasst. Beim in der Praxis anzutreffenden Schwachen Hedge wird eine Reihe kürzerer Hedges (z.B. täglich, wöchentlich) nacheinander gebildet.
II. Arten und Motive des Hedging
1. Die klassische Ausgangssituation
Die Situation, in der ein Hedge als Risikoabsicherung benötigt wird, sei nun wie folgt beschrieben: Zu einem gegebenen Zeitpunkt t sollen die Preisrisiken, die aus dem Verkauf (der Beschaffung) einer Position zu einem künftigen Zeitpunkt T zum dann gültigen Marktpreis PT entstehen, verringert werden. Dabei scheidet ein sofortiger Verkauf (ein Kauf) zum bekannten Marktpreis Pt aus. Vielmehr steht in t ein Terminkontrakt F zur Verfügung, der auf dem Terminmarkt zum bekannten Preis k gehandelt wird und in T zur Lieferung des jeweiligen Objekts (Underlying) führt. Beim Pure Hedge wird bei Kauf (Verkauf) einer bestimmten Anzahl des Kontraktes F das Underlying in einer definierten Menge geliefert (abgenommen), sodass PT = FT gilt. Vor dem Zeitpunkt T (t < s < T) und beim Cross Hedge generell sind Terminkurs Fs und Kassapreis Ps lediglich korreliert.
Sei nun q die Menge der Ressource (z.B. Aktien, Devisen, Waren) des Grundgeschäfts und x das Volumen, in dem Terminkontrakte als Gegengeschäft zum Zwecke des Hedging gezeichnet werden sollen (Spremann, K. 1991):
| - | Für x = q spricht man von einem vollständigen Hedge (Full Hedge, auch 1:1 Hedge). | | - | Für 0 < x < q spricht man von einem Normal Hedge. | | - | Wenn zusätzlich zur bereits bestehenden long (short) Position im Grundgeschäft eine long (short) Position auf dem Terminmarkt aufgebaut wird, d.h. x < 0 gewählt wird, spricht man von einem Texas Hedge. Dieser Hedge dient nicht zur Risikoverringerung sondern erhöht das bestehende Positionsrisiko. | | - | Wenn die Absicherungsposition auf dem Terminmarkt das Volumen des Grundgeschäfts übersteigt, d.h. x > q gewählt wird, so bezeichnet man dies als Reversed Hedge. Dabei wird das Preisrisiko der Position nicht nur verringert, sondern zusätzlich zum Basisrisiko des Hedge ein gegenläufiges Preisrisiko für das Volumen x – q erzeugt. |
Das Gesamtvermögen des Hedgers nach Verkauf von x Terminkontrakten beträgt

Die Hedge Ratio ist h = – x / q und sein aus heutiger Sicht risikobehaftetes Endvermögen ist
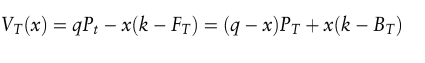
Beim Pure Hedge gilt stets BT = FT – PT = 0. Der Wert der Vermögensposition ist für beliebige Werte x außer für x = q unsicher . Wählt der Hedger x = q und damit den 1:1 Hedge, so verbleibt ihm der sichere Betrag VT(q) = qk. Beim Cross Hedge behält er das Basisrisiko. Sein Endvermögen beträgt dann VT(q) = q(k – BT).
2. Optimales Hedgen beim Pure Hedge
Welches Hedgingvolumen x sollte der mit dem Preisrisiko konfrontierte Entscheider wählen? Sollte er über den vollständigen Hedge das Preisrisiko in vollem Umfang eliminieren? Ein extrem risikoaverser Entscheider wird dies auf jeden Fall tun, unabhängig davon, wie der Erwartungswert des Endvermögens von der Entscheidungsvariablen x abhängt. Versucht er jedoch, seinen aus dem Hedging erwachsenden Nutzen zu maximieren, so wird er x unter Anwendung des Erwartungswert-Varianz-Kriteriums (Bamberg, G./Spremann, K. 1981) als Lösung des Maximierungsproblems
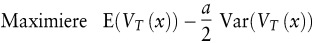
bestimmen (Spremann, K. 1986), wobei
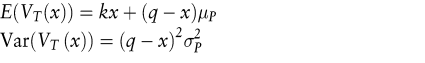
sind. Der Parameter a > 0 entspricht der individuellen Risikoaversion. Die Parameter μ, σ und σ2 sind der Erwartungswert, die Standardabweichung und die Varianz des Kassapreises P.
Die Lösung x* ist das Maximum einer quadratischen Funktion in x
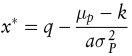
Einen vollständigen Hedge wird der Entscheider nur noch wählen, wenn Hedgen „ billig “ ist, d.h. der Terminkurs k dem erwarteten Preis μP entspricht, oder er unendlich risikoavers ist. In allen anderen Fällen liegt das optimale Hedgingvolumen im Bereich des Normal Hedge 0 < x < q.
3. Optimales Hedgen beim Cross Hedge
Nun seien der Terminpreis F und der Kassapreis P lediglich positiv korreliert. Für den Entscheider geht es nun darum, das Preisrisiko P im Volumen q zu behalten oder in einem gewissen Umfang durch den Verkauf von x Terminkontrakten F in das Basisrisiko einzutauschen. Man erhält das Maximierungsproblem
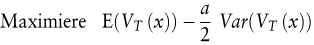
nunmehr mit
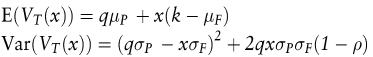
Die Parameter μ, σ und σ2 sind Erwartungswert, Standardabweichung und Varianz des jeweiligen Subskripts. ρ ist der Korrelationskoeffizient zwischen F und P. Lediglich für den Fall des Perfect Hedge mit einem Korrelationskoeffizienten ρ = 1 ergibt sich die Optimallösung als risikominimierender Hedge 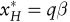 (variance minimizing hedge ratio). In allen anderen Fällen ist (variance minimizing hedge ratio). In allen anderen Fällen ist
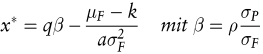
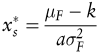 heißt Spekulationswunsch. Die Differenz μF – k im Zähler des Spekulationswunsches heißt Spekulationsprämie. Der risikominimierende Hedge entspricht umso mehr dem Full Hedge, je höher die Korrelation zwischen Kassa- und Terminpreis ist, wenn die Varianzen beider Größen übereinstimmen, was häufig ungefähr der Fall ist. Der Spekulationswunsch steigt mit der Risikoprämie und fällt mit der Risikoaversion des Hedgers und dem Risiko des Terminkontraktes. heißt Spekulationswunsch. Die Differenz μF – k im Zähler des Spekulationswunsches heißt Spekulationsprämie. Der risikominimierende Hedge entspricht umso mehr dem Full Hedge, je höher die Korrelation zwischen Kassa- und Terminpreis ist, wenn die Varianzen beider Größen übereinstimmen, was häufig ungefähr der Fall ist. Der Spekulationswunsch steigt mit der Risikoprämie und fällt mit der Risikoaversion des Hedgers und dem Risiko des Terminkontraktes.
Für eine ausführliche Diskussion weiterer Hedgingmodelle und damit zusammenhängender Produktionsentscheidungen (optimale simultane Wahl von q und x) wird auf Spremann (Spremann, K. 1991) und Kürsten (Kürsten, W. 1997a; Kürsten, W. 1997b verwiesen.
III. Hedging als Teil des Risikomanagements
Die Wahl von Hedgingstrategien ist neben der Risikomessung ein wesentlicher Teil des Risikomanagements (Steiner, M./Bruns, C. 2002). Neben dem Einsatz von Forward- und Futureskontrakten spielt das Hedging mit Optionen eine bedeutende Rolle. Hier unterscheidet man ebenfalls die statische Strategie als Absicherung durch Kauf von Verkaufsoptionen (long put) und dynamische Strategien (long put und short call) zum Delta Hedging im Rahmen der Portfolio Insurance.
Die in der Praxis verwendeten Strategien bauen auf Annahmen wie die korrekte Bewertung von Optionen und die Vollständigkeit der Märkte auf. Außerdem wurden darüber hinaus Hedgingmodelle für unvollständige Märkte entwickelt, z.B. zur Absicherung von Ansprüchen aus einer geschriebenen Kaufoption (z.B. Superhedging). Hedgingmodelle, die als Risikomaße nicht die Varianz, sondern Shortfall-Maße oder den Value-at-Risk verwenden, wurden ebenfalls vorgestellt; außerdem Modelle, die das Absicherungsziel mit einer vorgegebenen Maximalwahrscheinlichkeit verfehlen (Quantile Hedging, siehe Föllmer, H./Leukert, P. 1999).
Literatur:
Bamberg, G./Spremann, K. : Implications of Constant Risk Aversion, in: ZOR 1981, S. 205 – 224
Ederington, L .H. : The Hedging Performance of the New Futures Markets, in: JoF 1979, S. 157 – 170
Föllmer, H./Leukert, P. : Quantile Hedging, in: Finance and Stochastics 1999, S. 251 – 273
Johnson, L.L. : The Theory of Hedging and Speculation in Commodity Futures, in: REStud. 1960, S. 139 – 151
Kürsten, W. : Standardhedging, Simultanhedging und Portefeuille-Theorie, in: WiSt 1997a, H. 3, S. 119 – 123
Kürsten, W. : Hedgingmodelle, Unternehmensproduktion und antizipatorisch-simultanes Risikomanagement, in: ZfbF 1997b, Sonderheft 38 „ Bewertung und Einsatz von Finanzderivaten “ , S. 127 – 154
Spremann, K. : Produktion, Hedging, Spekulation – Zu den Funktionen von Futures-Märkten, in: ZfbF 1986, S. 443 – 464
Spremann, K. : Kann man mit Terminkontrakten hedgen? in: ZfbF 1991, S. 295 – 312
Stein, J. L. : The Simultaneous Determination of Spot and Futures Prices, in: AER 1961, S. 1012 – 1025
Steiner, M./Bruns, C. : Wertpapiermanagement, 8. A., Stuttgart 2002
Steiner, M./Meyer, F. : Hedging mit Financial Futures, in: Handbuch des Finanzmanagements, hrsg. v. Gebhardt, G./Gerke, W./Steiner, M., München 1993, S. 575 – 586
Working, H. : Futures Trading and Hedging, in: AER 1953, S. 314 – 343
|