|
Value-at-Risk
Inhaltsübersicht
I. Grundlagen und Ziele der Berechnung
II. Verfahren
III. Aufsichtsrechtliche Bedeutung
IV. Beurteilung der Aussagekraft
I. Grundlagen und Ziele der Berechnung
1. Definition des Value-at-Risk
Der Value-at-Risk (VaR) ist neben der Varianz die inzwischen wohl bekannteste Kennzahl zur Beschreibung des Risikos eines Wertpapierhandelsbestandes oder allgemein eines Portfolios risikobehafteter Anlagen. Der VaR dient als Grundlage für die Quantifizierung des sog. Marktrisikos im Bereich der Kreditinstitute mit bankinternen Risikomess- und Steuerungsmodellen (Johanning, 1998). Durch die in der 6. KWG-Novelle geschaffene Möglichkeit die Kennziffer als Grundlage aufsichtsrechtlicher Meldeverfahren und zur Ermittlung der erforderlichen Eigenkapitalunterlegung zu verwenden, hat die Ermittlung des Value-at-Risk für das Risikomanagement in Kreditinstituten zentrale Bedeutung erlangt. „ Risikomodelle sind zeitbezogene stochastische Darstellungen der Veränderungen von Marktkursen, -preisen oder -zinssätzen und ihrer Auswirkungen auf den Marktwert einzelner Finanzinstrumente oder Gruppen von Finanzinstrumenten . . . “ (Bundesaufsichtsamt für das Kreditwesen, 1997a, §32). Eine überzeugende Übersetzung des Begriffs Value-at-Risk in die deutsche Sprache liegt allerdings nicht vor. Durch das BAKred [mittlerweile BaFin] wurde der Begriff potenzieller Risikobeitrag als Übersetzung für Value-at-Risk verwendet: „ Im Mittelpunkt eines eigenen Risikomodells steht die Kennzahl des Value at Risk, (VaR, gelegentlich auch Money at Risk, o.ä. genannt), die der Grundsatz I als potenziellen Risikobetrag bezeichnet. [. . .] indem der Value at Risk eine Schranke für potenzielle Verluste zwischen zwei vorgegebenen Zeitpunkten angibt, die mit einer vorgegebenen Wahrscheinlichkeit nicht überschritten wird. “ (Bundesaufsichtsamt für das Kreditwesen, 1997b, S. 170).
Der Value-at-Risk ist also die Bezeichnung für ein in Geldeinheiten ausgedrücktes Verlustpotenzial, das durch das Risiko von Marktpreisänderungen der im Portfolio enthaltenen Anlagen gegeben ist und mit einer vorgegebenen Wahrscheinlichkeit nicht überschritten wird. Er stellt damit ein monetäres, in die Zukunft gerichtetes Risikomaß dar, das auf einer Wahrscheinlichkeitsverteilung für zukünftige Verluste basiert. Mit dem Begriff Verlustpotenzial wird leicht die „ irreführende Assoziation “ verbunden, dass es sich beim VaR um einen Maximalverlust handelt. Dies ist falsch, da der theoretische Verlust bei Lieferverpflichtungen oder Fremdwährungspositionen durchaus unbeschränkt sein kann (Huschens, 1999, S. 1). Der VaR muss also stets von der Angabe einer Restwahrscheinlichkeit begleitet werden, mit der ein den VaR übersteigender Verlust eintreten kann. Weiter ist für die praktische Verwendung des VaR zur Risikomessung eine Angabe über den zukünftigen Zeitpunkt erforderlich, zu dem der mit dem VaR gemessene Verlust eintreten kann.
Ziel der Value-at-Risk-Berechnung ist es nun, dieses Verlustpotenzial möglichst genau zu ermitteln, um es
(a) zur Grundlage der Risikoeinschätzung einzelner Portfolios, etwa des Handelsbestandes einzelner Händler, Gruppen oder Abteilungen und entsprechender Handelslimite zu machen (Morgan, 1996; Jorion, 2000);
(b) als Steuerungsinstrument und Basis für die Risk-Return-Kalkulation in Kreditinstituten zu verwenden (Johanning, 1998);
(c) im Rahmen interner Risikomodelle zur Erfüllung der aufsichtsrechtlichen Meldepflichten und zur Ermittlung der erforderlichen Eigenkapitalunterlegung zu verwenden (Bank für Internationalen Zahlungsausgleich (BIZ), 1996; Bundesaufsichtsamt für das Kreditwesen, 1997a).
2. Eigenschaften des Value-at-Risk
Der Value-at-Risk (VaR) einer Handelsposition bzw. eines Portfolios ist damit kurz gefasst
| - | der in Geldeinheiten ausgedrückte Verlustbetrag | | - | für eine vorgegebene Haltedauer (z.B. 10 Tage), | | - | der lediglich mit einer vorgegebenen Wahrscheinlichkeit (z.B. 5%) | | - | am Ende der Haltedauer überschritten wird. |
Eine formale Abbildung der Kennziffer und schließlich exakte Definition sollte die in dieser Aussage enthaltenen impliziten Eigenschaften ebenfalls hervorheben:
(a) Zunächst geht es bei der Bestimmung des VaR um die Wertänderung eines Portfolios über eine vorgegebene Haltedauer. Diese Wertänderung kann direkt durch den Portfoliowert für diesen Zeitpunkt oder indirekt über die Portfoliorendite für die Haltedauer ausgedrückt werden. In beiden Fällen ist der Wert der Verteilungsfunktion der jeweiligen Zufallsgröße zu bestimmen, welche den VaR und die vorgegebene Wahrscheinlichkeit verknüpft. Bei der Bestimmung des VaR ist darauf zu achten, dass diese statistische Quantileigenschaft gegeben ist.
(b) Weiter sollte der VaR die Eigenschaft der Eindeutigkeit besitzen, d.h. ein Geldbetrag und nicht etwa Intervall möglicher Verluste sein. Die Bestimmung des VaR ist damit die Aufgabe der statistischen Punktschätzung, auf Basis aktuell verfügbarer Daten eine Prognose des Quantils zu ermitteln. Solche Prognosen sind selbst mit einer statistischen Unsicherheit behaftet, sodass man statt von VaR-Berechnung besser von VaR-Schätzung sprechen sollte. Außerdem ist es möglich, dass der gesuchte Wert – etwa bei diskreten Verteilungen oder der Verwendung empirischer Verteilungen – nicht existiert oder nicht eindeutig ist. Dann muss ein nahegelegener Ersatzwert oder einer von mehreren in Frage kommenden Werten bestimmt werden. Die entsprechende Regel hierfür sollte jedoch ebenfalls eindeutig sein.
(c) Weiter ist als Eigenschaft die Nichtnegativität zu fordern. Zwar bezieht sich der VaR auf eine negative Wertentwicklungen des Portfolios (P&L, Profit and Loss), doch wird das Risiko als Absolutbetrag ausgedrückt. Wenn aus einem Portfolio mit Sicherheit nur Gewinne entstehen oder die Verlustwahrscheinlichkeit insgesamt geringer als die vorgegebene Wahrscheinlichkeitsschwelle ist, so ist der VaR mit dem Wert 0 anzusetzen.
Eine verbale Definition des VaR, welche die gewünschten Eigenschaften enthält (Huschens, 1999, S. 12), lautet dann: „ Value-at-Risk ist die kleinste nichtnegative Schranke für potenzielle Verluste am Ende einer Zeitspanne T, die mit einer vorgegebenen Mindestwahrscheinlichkeit 1-α nicht überschritten wird. “
3. Ziele der Value-at-Risk-Schätzung
Im Allgemeinen wird die Unsicherheit durch die Wahrscheinlichkeitsverteilung Pt+1 für die Periode t+1 in Verbindung mit der Zufallsvariablen Lt+1 = – ΔPt+1 = pt – Pt+1 dargestellt, welche die Gewinne und Verluste des Portfolios (Profit and Loss, P&L) bezeichnet.
In der Praxis ist die Vorhersage von Pt+1 abhängig von der Informationsmenge, die zur Zeit t vorliegt und wird durch eine Plug-In Methode bestimmt (Dawid, 1984). In diesem Fall ist Pt+1 das Ergebnis eines statistischen Prognosemodells, hier das VaR-Modell, welches aus einer (parametrisierten) Familie von Verteilungen besteht und durch 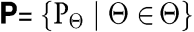 zusammen mit einer Vorhersageregel angegeben wird. Angenommen Pt+1 gehört zu so einer parametrisierten Verteilungsfamilie P, so werden die Schätzer zusammen mit einer Vorhersageregel angegeben wird. Angenommen Pt+1 gehört zu so einer parametrisierten Verteilungsfamilie P, so werden die Schätzer 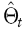 anhand der Vorhersageregel auf Basis einer Informationsmenge Ht, meist einer rollierenden Datenhistorie fester Länge n für alle t berechnet, d.h. Pt + 1(·) = P anhand der Vorhersageregel auf Basis einer Informationsmenge Ht, meist einer rollierenden Datenhistorie fester Länge n für alle t berechnet, d.h. Pt + 1(·) = P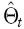 (· | Ht). Seien w die Vektoren der in der Datenhistorie enthaltenen relevanten Einflussgrößen für Pt (sog. Risikofaktoren), α die vorgegebene Überschreitungswahrscheinlichkeit und damit (1 – α) die Wahrscheinlichkeit, dass der Verlust den VaR nicht überschreitet. Die Haltedauer sei durch T und die Wahrscheinlichkeit durch Prob(·) bezeichnet. Dann lässt sich die vorstehende verbale Definition auch ausdrücken durch die formale VaR-Definition: (· | Ht). Seien w die Vektoren der in der Datenhistorie enthaltenen relevanten Einflussgrößen für Pt (sog. Risikofaktoren), α die vorgegebene Überschreitungswahrscheinlichkeit und damit (1 – α) die Wahrscheinlichkeit, dass der Verlust den VaR nicht überschreitet. Die Haltedauer sei durch T und die Wahrscheinlichkeit durch Prob(·) bezeichnet. Dann lässt sich die vorstehende verbale Definition auch ausdrücken durch die formale VaR-Definition:
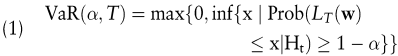
II. Verfahren der VaR-Berechnung
1. Einfache Analytische VaR-Ansätze
Die in der Praxis eingesetzten Methoden zur Bestimmung des gesuchten Quantils der Verteilung des Portfoliowertänderungen unterscheiden sich nach
| - | Bestimmung des Positionswertes einzelner im Portfolio enthaltenen Positionen (Instrumentenmapping), | | - | Art und Anzahl der verwendeten Risikofaktoren, | | - | die für die Veränderung der Risikofaktoren (Risikofaktorrenditen) unterstellte Verteilung und | | - | deren Einfluss auf den Portfoliowert (Risikofaktormapping), | | - | Zuordnung einzelner Instrumente zum Portfolio (Positionsmapping), | | - | Parametrisierung der Verteilung, | | - | Prognosehorizont, | | - | Annahmen für die Renditeverteilungen (Data Generating Process, DGP). | a) Lineare Portfolios – Delta-Normal-Methode
Die Grundannahme vieler in der Praxis eingesetzter Modelle (vgl. z.B. RiskMetrics?; Morgan, 1996), lautet: Die Wertänderung des Portfolios am Ende einer gegebenen Periode hängt linear von den Renditen einer festen Anzahl von Risikofaktoren ab. Diese Annahme (lineare Faktorsensitivität) macht die Schätzung der Abhängigkeiten z.B. durch ökonometrische Modelle einfacher und ist in theoretischen Modellen wie z.B. dem CAPM für manche Instrumente (z.B. Aktien-Beta als Abhängigkeit zwischen Aktien und Marktindex), ebenfalls zu finden.
Annahme 2 lautet: Die Risikofaktoränderungen sind multivariat normalverteilt. Diese Annahme hat zur Konsequenz, dass auch die Portfoliorenditen bei linearer Abhängigkeit von den Risikofaktoren normalverteilt sind. Eine weitere für kurze Prognosezeiträume tolerierbare Vereinfachung ist: Der Erwartungswert der Portfoliorenditen wird gleich 0 gesetzt. Damit wird eine Normalverteilung mit Erwartungswert 0 unterstellt, sodass als einziger Parameter noch die Standardabweichung geschätzt werden muss.
In der Praxis umfasst die Datenhistorie zur Schätzung der Parameter von P die letzten n = 250 Handelstage. Ein Beispiel für P ist die aus RiskMetrics? (Morgan, 1996) bekannte Delta-Normal-Methode, d.h. die betrachteten Portfolios bestehen aus linearen (oder linearisierten) Instrumenten und die gemeinsame Verteilung der Log-Preis Veränderungen der Basiswerte Y, d.h. die Yt+1 gehorchen einer (bedingten) multivariaten Normalverteilung N (0, Σt).
Der Einfachheit halber betrachten wir nun eine Anteilsposition von λt in einem einzigen Asset, dessen Marktwert bei xt liegt. Die bedingte Verteilung von Lt+1 für diese Position mit der offenen Position (Exposure) 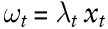 ist (approximativ) ist (approximativ)
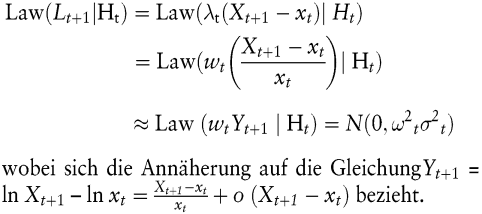
Die Verallgemeinerung auf ein Portfolio mit linearen Assets ist offensichtlich. Deshalb gehört die Verteilung der Zufallsvariablen 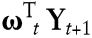 zur Familie der Normalverteilungen zur Familie der Normalverteilungen
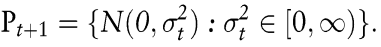 b) Nichtlineare Portfolios – Delta-Gamma-Approximation
Bei nichtlinearen Abhängigkeiten zwischen den Risikofaktoren und dem Positionswert versucht man eine Annäherung durch eine quadratische Approximation, z.B. durch eine Taylor-Approximation 2. Ordnung bezüglich der Risikofaktoren.
Bei geringen Veränderungen der Risikofaktoren ist diese Anpassung ausreichend. Probleme entstehen für erhebliche Änderungen, da abseits des aktuellen Positionswerteswertes die Delta-Gamma-Approximation eine geringe Genauigkeit aufweisen kann. Außerdem führt diese Umrechnung zu einem Verlust der Normalverteilungseigenschaft für die Positionsrendite, sodass die Portfoliorendite nur noch für eine große Anzahl von Einzelpositionen oft näherungsweise normalverteilt ist. In der Praxis werden weitere Ableitungen nach dem Positionswert des Portfolios z.B. nach der Volatilität (Vega) und der Zeitwertverlust (Theta) von Optionspositionen berücksichtigt (z.B. Locarek-Junge, 1998).
III. Aufsichtsrechtliche Bedeutung
1. Prognoseziele und VaR-Modelle
Mit der Umsetzung von Value-at-Risk (VaR) Modellen wurde ein neues Kapitel im Risikomanagement in Kreditinstituten begonnen. Das Ziel ist es, die Unsicherheit über den Betrag, der in einer bestimmten Zeit in einem Portfolio gewonnen oder verloren werden kann, zu quantifizieren. Das Ziel der VaR-Analyse ist im obigen Kontext der vereinfachten linearen VaR-Modelle, 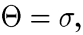 zu schätzen und dabei eine Vorhersageregel aufzustellen. Für Lt+1 ist dafür folgender Rahmen angenommen, siehe RiskMetrics? Morgan, 1996): zu schätzen und dabei eine Vorhersageregel aufzustellen. Für Lt+1 ist dafür folgender Rahmen angenommen, siehe RiskMetrics? Morgan, 1996):
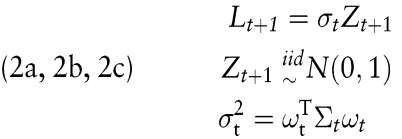
wobei Σ und σ2t die bedingten Varianzen angeben, also Ht-messbare Funktionen. Für eine gegebene (n × d) Datenmatrix Xt = {xi},i=t--n+1,...,t von Realisationen der zugrundeliegenden Renditevektoren mit Dimension d werden zwei Schätzer für Σt betrachtet. Der erste ist ein naiver Schätzer, welcher auf dem gleitenden Durchschnitt (Rectangular Moving Average, RMA) beruht,
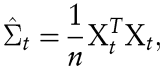
wobei zu beachten ist, dass der Erwartungswert der Renditen mit Null angenommen wurde. Der zweite, von Taylor zur Prognose der Volatilität empfohlene Schätzer beruht auf einem exponentiell gewichteten Schema (Exponential Moving Average, EMA), welches auf die Datenmatrix

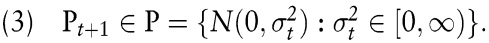
ergibt (Taylor, 1986).
VaR-Modelle leisten auf natürliche Weise einen Beitrag zu verschiedenen Aspekten des Risikomanagements. Deshalb sind eine Reihe von interessierenden Parametern – hergeleitet aus Pt+1 – relevant. Die jeweilige Auswahl leitet sich aus den spezifischen Prognosezielen her. Diese können durch externe (z.B. regulatorische) oder interne Anforderungen und Bedürfnisse (Limits, Optimierung) bestimmt sein.
2. Beurteilung der Qualität von VaR-Modellen a) Datenqualität
Zielgröße von VaR-Modellen ist eine Wahrscheinlichkeitsprognose über Portfoliowertänderungen über einen bestimmten Prognosehorizont. Damit kommt der Bewertung der Finanzinstrumente des Portfolios zu zwei verschiedenen Zeitpunkten eine zentrale Bedeutung zu. Die Bewertung kann auf sog. Instrumentmodellen (mark-to-model) basieren oder auf Marktpreise der Instrumente rekurrieren (mark-to-market). Das Modellhafte der Instrumentenbewertung erfordert die Prüfung der Angemessenheit der zu Grunde liegenden Bewertungsverfahren sowie die vollständige, richtige und zeitnahe Erfassung der Geschäfte bzw. Positionen und der Marktdaten, z.B. eine geeignete Behandlung asynchroner Daten unterschiedlicher Zeitzonen oder fehlender Werte in Datenreihen. b) Prognosequalität
Zur Beurteilung von Prognoseverfahren dienen Backtestingverfahren. Obwohl es naheliegend ist, die Beurteilung der Prognosegüte an den geschätzten Parameter zu knüpfen, wurden effizientere Verfahren vorgeschlagen, welche auf der ganzen Prognoseverteilung und nicht nur auf einem Parameter beruhen (Dawid, 1984; Sellier-Moiseiwitsch, 1993; Crnkovic, /Drachman, 1996). Für eine gegebene Folge von Paaren (Pt, lt), wobei lt die Realisation von Lt bezeichnet, liefert eine Vorhersageregel gute Ergebnisse, wenn die Stichprobe u = (ut)kt=1 = (Ft(lt))kt=1 sich wie eine iid-Stichprobe aus U[0,1] verhält, wobei Ft+1 die Verteilungsfunktion von Pt+1 bezeichnet. Die statistischen Verfahren unterscheiden sich je nachdem, ob man eine iid-Annahme trifft und Verteilungseigenschaften überprüft, oder ob der Schwerpunkt auf der Überprüfung der iid-Eigenschaften liegt.
IV. Beurteilung der Aussagekraft
Eine zufriedenstellende Prognosequalität wird oft als angemessenes VaR-Modell interpretiert. In einer erst vor kurzem entstandenen Arbeit nennen Engle und Manganelli verschiedene Spezifikationstests für VaR-Modelle, welche die iid-Eigenschaften untersuchen (Engle, /Manganelli, 1999). In der Praxis lassen jedoch die Daten zumeist ein klares Bild entstehen und explorative Untersuchungsmethoden reichen gewöhnlich aus, um die Prognosequalität zu beurteilen. Dennoch sei hier vorgeschlagen, den erwarteten Shortfall von Lt+1, als den interessierenden Parameter zu betrachten und Backtestingmethoden zu verwenden, die mit diesem Parameter zusammenhängen. Der erwartete Shortfall – genannt Tail-VaR – ist für das Delta-Normal Modell definiert als
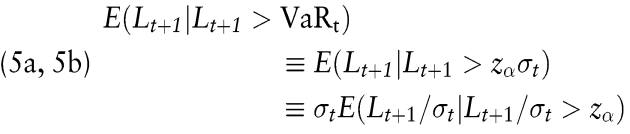
wobei zα das α-Quantil einer Standardnormalverteilung ist. Es gibt drei Gründe für die Verwendung dieser Größe:
Erstens haben McAllister und Mingo die Vorteile von (5) gegenüber VaR herausgearbeitet (McAllister, /Mingo, 1996), wenn man diese Parameter in den Nenner von Risiko-Perfomance-Maßen integriert, z.B. ein Sharpe-Ratio oder eine RAROC-Ziffer (Matten, 2000), – die ökonomische Motivation.
Zweitens haben Artzner et al. hervorgehoben, dass (5) ein kohärentes Risikomaß approximiert (Artzner, /Delbean, /Eber, /Heath, 1997).
Drittens betont Leadbetter in diesem Zusammenhang den Bedarf nach Verwendung der Höhe der Limitüberschreitungen in der Modellbeurteilung durch die Aufsicht und kritisiert jene Methoden, die nur auf der Anzahl der Überschreitungen beruhen und so die Höhe der Überschreitung vernachlässigen – statistische Argumente (Leadbetter, 1995).
Neben dem VaR kann man aus der Prognoseverteilung auch andere Risikomaße ableiten. In diesem Rahmen werden verschiedene Prognoseziele inklusive Value-at-Risk und Shortfall diskutiert. In einer aktuellen Arbeit (Härdle, /Stahl, 1999) wurde eine auf dem Shortfall basierende Backtestingmethode, entwickelt und auf die VaR-Prognosen eines realen Portfolios angewandt. Die Analyse zeigte, dass Backtestingverfahren, die auf Shortfall basieren, sehr sensibel im Hinblick auf zugrunde liegende Verteilungsannahmen sind.
Es ist jedoch insgesamt unbefriedigend, für die qualitative Beurteilung von Value-at-Risk-Modellen ein anderes Maß (Tail-VaR) zu verwenden als bei der Anwendung der Modelle zum Zweck der Risikomessung. Die Lösung ist aber nicht die Verwendung des VaR (und als Gütekriterium die Anzahl der VaR-Überschreitungen) bei der Risikomessung, sondern die Weiterentwicklung der Risikomodelle durch eine Kombination der Kenngrößen VaR und Tail-VaR.
Literatur:
Artzner, P./Delbean, F./Eber, J.-M./Heath, D. : Thinking Coherently, in: Risk, Vol. 10, Nr. 11, 1997, S. 68 – 71
Bundesaufsichtsamt für das Kreditwesen, : Bekanntmachung über die Änderung und Ergänzung der Grundsätze über das Eigenkapital und die Liquidität der Kreditinstitute vom 29. Oktober 1997, Berlin 1997a
Bundesaufsichtsamt für das Kreditwesen, : Erläuterungen zur Bekanntmachung über die Änderung und Ergänzung der Grundsätze über das Eigenkapital und die Liquidität der Kreditinstitute vom 29. Oktober 1997, Berlin 1997b
Bank für Internationalen Zahlungsausgleich (BIZ), : Amendment to the Capital Accord to incorporate Market Risks, Basel 1996
Bank für Internationalen Zahlungsausgleich (BIZ), : A New Capital Adequacy Framework, Basel 1999
Crnkovic, C./Drachman, : A Universal Tool to Discriminate Among Risk Measurement Techniques, RISK Magazine, 1996
Dawid, A P. : The prequential approach. J.R. Statist. Soc. A., 1984, S. 278 – 292
Engle, R.F./Manganelli, S. : CAViaR: Conditional Autoregressive Value Risk by Regression Quantiles. Pre-print, University of California, San Diego 1999
Härdle, W./Stahl, G. : Backtesting Beyond VaR, in: Measuring Risk in Complex Stochastic Systems, Lecture Notes in Statistics, 147, 1999, Eds.: Franke, J.et al. 119 – 129
Huschens, S. : Anmerkungen zur Value-at-Risk-Definition, Dresdner Beiträge zu Quantitativen Verfahren 28/99, Dresden 1999
Johanning, L. : Value-at-Risk zur Marktrisikosteuerung und Eigenkapitalallokation, Bad Soden 1998
Jorion, P. : Value at Risk, 2nd Ed., Chicago 2000
Morgan, : RiskMetrics? – Technical Document, 4. A., New York 1996
Leadbetter, M.R. : On high level exceedance modeling and tail inference, in: Journal of Planning and Inference 1995, S. 247 – 260
Locarek-Junge, H. : Risikomessung in Portefeuilles mit Derivaten, in: Oehler, A. (Hrsg.): Credit Risk und Value-at-Risk Alternativen, Stuttgart 1998, S. 201 – 227
Locarek-Junge, H. : Mathematische Methoden des Marktrisikomanagements, in: Gaul, W./Schader, M.: Mathematische Methoden der Wirtschaftswissenschaften, Heidelberg 1999, S. 258 – 271
Matten, C. : Managing Bank Capital, 2nd Ed., Chichester 2000
McAllister, P.H./Mingo,, : Bank Capital Requirements for Securitized Loan Portfolios, in: JBF 20, 1996, S. 1381 – 1405
Sellier-Moiseiwitsch, F. : Sequential Probability Forecasts and the Probability Integral Transform, Int. Stat. Rev. 61, 1993, S. 395 – 408
Taylor, S.J. : Modelling Financial Time Series, 1986
|