|
Risikomaße
Inhaltsübersicht
I. Risiko als eigenständiges Konzept
II. Ausgewählte Risikomaße
III. Analogien zwischen Risikomaßen und Ungleichheits- bzw. Armutsmaßen
I. Risiko als eigenständiges Konzept
Die Erörterung des Themas Risikomaße macht zunächst eine inhaltliche Abgrenzung des Begriffs Risiko erforderlich. Die in den folgenden Ausführungen vorgestellten Risikomaßzahlen werden fast durchweg aus (Rendite-) Verteilungsfunktionen abgeleitet. Hierbei wird der Erwartungswert einer Renditeverteilung selbst nicht als Risiko klassifiziert. Vielmehr wird lediglich die Gefahr der Abweichung von diesem Erwartungswert oder des Unterschreitens eines i.d.R. niedrigeren Zielwertes als Risiko verstanden. Bei einem solchen Risikoverständnis lassen sich Kenngrößen wie z.B. die Duration nicht als Risikomaß bezeichnen. Vereinfacht ausgedrückt misst die Duration die relative Änderung des Marktwertes von festverzinslichen Wertpapieren als Folge einer Änderung des Marktzinsniveaus. Insofern hat sie zwar einen risikorelevanten Informationsgehalt, gleichwohl stellt sie jedoch ein Sensitivitätsmaß dar.
Des Weiteren setzt die Beschäftigung mit der Risikomessung quasi implizit voraus, dass Risiko eine eigenständige relevante Größe ist. Das ist keinesfalls trivial. Auf vollkommenen und vollständigen Kapitalmärkten (Kruschwitz, 1999, S. 37ff.; Schmidt, R. H./Terberger, E. 1997, S. 91ff.) können beispielsweise Investoren durch Diversifikations- und Hedging-Aktivitäten die gewünschte Risikoallokation transaktionskostenfrei selbst erzeugen. Deutlich wird dieses beispielsweise in der State-Preference-Theorie. Die arbitragefreien Marktpreise neuer Finanztitel sind dort mithilfe der Zustandspreise und der zustandsabhängigen Rückzahlungen der Finanztitel berechenbar. Investitionsentscheidungen werden ohne Bezug auf eine Risikogröße allein auf Basis von Preisen getroffen.
Im Rahmen der Erwartungsnutzentheorie, d.h. für Entscheider, die nach dem Bernoulli-Prinzip handeln, ist ein Risikomaß ebenfalls unnötig; denn sie maximieren den erwarteten Nutzen. In der Literatur sind allerdings viele Fälle dokumentiert, in denen das beobachtete Entscheidungsverhalten nicht zur Erwartungsnutzentheorie passt (Weber, M. 1990, S. 35ff.).
Eine nahe liegende und gebräuchliche Alternative zur Verwendung der Erwartungsnutzentheorie ist die Arbeit mit Risiko-Wert-Modellen (Brachinger, H. W./Weber, M. 1997; Sarin, R. K./Weber, M. 1993). In diesen Modellen erfolgt eine Beurteilung von Entscheidungsalternativen auf Basis von Funktionen, in die eine Wertkennzahl (z.B. eine erwartete Rendite) und eine Risikokennzahl (z.B. ein Maß für die Streuung der Renditen) eingehen. Ein besonders wichtiger Spezialfall dafür ist das (μ,σ)-Prinzip, das in kapitalmarkttheoretischen Modellen häufig benutzt wird. Als Risikomaß findet dort die Varianz bzw. die Standardabweichung Verwendung. Alternativ benutzen Kaduff/Spremann in einem vergleichbaren Ansatz die Ausfallwahrscheinlichkeit relativ zu einer Zielgröße T als Risikogröße (Kaduff, J. V./Spremann, K. 1996).
Entscheidungstheoretisch ist zur Anwendung solcher Modelle gleichwohl anzumerken, dass sich der erwartete Nutzen (nur) in Spezialfällen in eine Wert- und eine Risikogröße zerlegen lässt (Sarin, R. K./Weber, M. 1993). Der (μ,σ)-Ansatz liefert z.B. lediglich für quadratische Nutzenfunktionen oder normalverteilte Renditen gleiche Auswahlentscheidungen wie die Erwartungsnutzentheorie (Franke, /Hax, 1999).
Insgesamt ist die Fragestellung, welche Risikomaße mit der Erwartungsnutzentheorie vereinbar sind, aus entscheidungstheoretischer Sicht sehr interessant. Von Vereinbarkeit eines Risikomaßes R mit der Erwartungsnutzentheorie kann gesprochen werden, wenn für zwei Verteilungen X und Y mit gleichem Erwartungswert Folgendes gilt: Falls X für jeden Entscheidungsträger mit einer monoton wachsenden und streng konkaven Nutzenfunktion einen größeren erwarteten Nutzen liefert als Y, so muss R(X) < R(Y) gelten. Besteht zwischen den Verteilungen X und Y die obige Beziehung, so liegt stochastische Dominanz zweiter Ordnung vor (Hadar, /Russel, 1969; Hadar, /Russel, 1971; Hanoch, G./Levy, H. 1969; Rothschild, M./Stiglitz, J. E. 1970).Vereinbar mit der Erwartungsnutzentheorie ist ein Risikomaß folglich dann, wenn es für Verteilungen mit gleichem Erwartungswert eine Anordnung entsprechend der stochastischen Dominanz zweiter Ordnung wiedergibt. Die stochastische Dominanz selbst ist zur Risikomessung kaum geeignet, da sie lediglich eine Teilordnung mit ordinalskalierten Risikowerten liefert.
II. Ausgewählte Risikomaße
1. Gesamtbetrachtung versus Downside-Betrachtung
Varianz und Standardabweichung einer Verteilung messen die Streuung um den Mittelwert, beziehen sich also auf die gesamte Verteilung. Dieses Verständnis von Risiko ist nicht unumstritten. Mülhaupt definiert Risiko als „ die Gefahr einer negativen Abweichung des tatsächlichen vom erwarteten Wert eines Ereignisses “ (Mülhaupt, L. 1980, S. 188). Abweichungen nach oben werden im Rahmen einer solchen Konzeption oft als Chance bezeichnet. Die Vorstellung von Risiko als Verlustgefahr liegt auch den Safety-First-Überlegungen zugrunde, auf die Kaduff/Spremann mit einer Reihe von Literaturverweisen eingehen (Kaduff, J. V./Spremann, K. 1996). Sieht man dementsprechend nur auf den unteren Teil einer Verteilung, so konzentriert man sich auf das Downside-Risiko bzw. bei Festlegung einer Zielgröße und Betrachtung der negativen Abweichungen davon auf das Shortfall-Risiko.
Welche Konzeption richtig ist, kann nicht abstrakt entschieden werden, sondern ist jeweils mit Blick auf die konkrete Anwendung bzw. die Zielsetzung festzulegen. Für eine Bankenaufsicht, die durch Risikobegrenzung die Sicherheit eines Finanzsystems gewährleisten will, ist beispielsweise die Verwendung von Downside-Risikomaßen plausibel. Ein Aktienhändler mag demgegenüber das Risiko u.U. besser mit einem Gesamtrisikomaß messen.
2. Messung des Gesamtrisikos
Verantwortlich für die weite Verbreitung von Varianz und Standardabweichung zur Quantifizierung des Gesamtrisikos ist neben ihrer einfachen Berechnungsvorschrift nicht zuletzt ihre Berücksichtigung in den bekannten Erklärungs- und Bewertungsmodellen der neoklassischen Kapitalmarkttheorie. So werden diese sowohl im CAPM (z.B. Copeland, T. E./Weston, J. F. 1988) als auch in der Portfoliotheorie nach Markowitz (Markowitz, 1952; Markowitz, H. M. 1991) und bei der Optionsbewertung nach Black-Scholes (z.B. Steiner, /Bruns, 2000) zur Quantifizierung des Risikos von Wertpapieren eingesetzt. Als Maß für die Streuung von Renditen um ihren Erwartungswert erfassen beide sowohl negative als auch positive Abweichungen vom Erwartungswert als Risiko. Für eine stetig verteilte Rendite mit dem Erwartungswert μ und der zugehörigen Dichtefunktion f(r) lässt sich ihre Varianz formulieren als
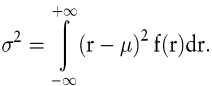
Die Standardabweichung ergibt sich dann als Quadratwurzel der Varianz. Eine besondere Bedeutung kommt der Quantifizierung des Gesamtrisikos mittels Varianz und Standardabweichung bei Vorliegen normalverteilter Renditen zu. In diesem Fall lässt sich ihre Verteilung nämlich vollständig durch ihre ersten beiden Momente – Erwartungswert und Standardabweichung – beschreiben. Hingegen sind bei nicht normalverteilten Renditen u.U. weitere Momente zur Verteilungsbeschreibung notwendig. Hierzu wird regelmäßig auf die Schiefe als drittes und die Kurtosis als viertes Moment einer Verteilung zurückgegriffen (Hartung, J./Elpelt, B./Klösener, K.-H. 1999, S. 118 f.; Kreyszig, E. 1979, S. 94; Sachs, L. 1997, S. 167 ff.).
3. Messung des Downside-Risikos a) Semivarianz
Im Unterschied zu den Gesamtrisikomaßen konzentrieren sich die Downside-Risikomaße auf den (noch näher zu definierenden) unteren Bereich einer Verteilung. Ausgehend von der Varianz lässt sich relativ einfach ein Downside-Risikomaß konstruieren, indem nur die Werte berücksichtigt werden, die den Erwartungswert unterschreiten. Die so genannte (untere) Semivarianz (z.B. Franke, /Hax, 1999; Serf, B. 1995) entspricht dem Erwartungswert der quadrierten negativen Abweichungen vom Erwartungswert μ und lässt sich für eine stetige Dichtefunktion f(r) der Renditen schreiben als
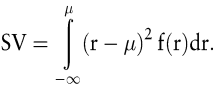
Der Begriff der Semivarianz wird auch relativ häufig für den allgemeineren Fall verwendet, in dem die negativen Abweichungen von einem zuvor zu definierenden Target T, hier: einer Zielrendite, zugrunde gelegt werden (Markowitz, H. M. 1991). Sie entspricht dann dem Lower Partial Moment zweiter Ordnung (s.u.). Meyer bezeichnet die auf den Erwartungswert bezogene Semivarianz daher auch als Semivarianz im engeren Sinne (Meyer, C. 1999, S. 47).
Das mit der Semivarianz SV gemessene Risiko steigt, wenn größere negative Abweichungen vom Erwartungswert zu verzeichnen sind. Hingegen bleibt es unbeeinflusst von Renditeänderungen oberhalb des Erwartungswertes. Aus entscheidungstheoretischer Sicht wird die Semivarianz kritisch beurteilt, da der obere Teil der Verteilung quasi „ abgeschnitten “ wird. Entscheidungsrelevante Informationen können so verloren gehen (Franke, /Hax, 1999).
Auswahlentscheidungen auf Basis dieses asymmetrischen Risikomaßes führen bei symmetrischen Verteilungen (mit identischen Erwartungswerten) zu denselben Ergebnissen wie Entscheidungen auf der Grundlage der Varianz. Die Semivarianz weist jedoch aufgrund des zugrunde liegenden asymmetrischen Risikobegriffs einen Vorteil für den Fall schiefer Verteilungen auf. b) Lower Partial Moments
Eine wichtige Kategorie der Downside-Risikomaße bilden die Lower Partial Moments, mit deren Hilfe der Bereich einer Verteilung unterhalb eines festzulegenden Targets charakterisiert wird. Abhängig von der Anzahl n der berücksichtigten Momente der Verteilung lassen sich verschiedene Ausprägungen der Lower Partial Moments unterscheiden. Der Lower Partial Moment n-ter Ordnung LPMn einer Dichtefunktion f(r) der Renditen gibt das n-te Moment der Abweichung der Rendite r von einer Zielrendite T an:
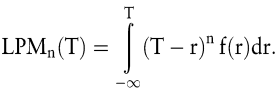
Zur Berechnung dieser Risikomaße sind zwei Parameter zu bestimmen: die Zahl n der berücksichtigten Momente sowie die Zielrendite T (Portmann, T. 1999). Je höher n gewählt wird, desto stärker ist die Gewichtung großer Unterschreitungen der Zielrendite. Für den Fall n = 0 lässt sich obige Formel vereinfachen zu
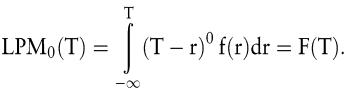
Der LPM0 gibt den Wert der Verteilungsfunktion für die Zielrendite an und entspricht damit der Wahrscheinlichkeit, dass maximal eine Rendite in Höhe von T erreicht wird. Es wird in diesem Zusammenhang auch von Downside-, Shortfall- oder Ausfallwahrscheinlichkeit gesprochen. Der LPM0 liegt dem Safety First-Ansatz von Roy zugrunde (Roy, A.D. 1952). Das Ausmaß der negativen Abweichungen von der Zielrendite wird beim LPM0 nicht berücksichtigt.
Im Gegensatz dazu geht die Höhe der Target-Verfehlungen in die Berechnung der höheren Lower Partial Moments ein. Der LPM1 stellt den Erwartungswert der Zielverfehlung (Downside-Erwartungswert) dar. Er lässt sich graphisch als Fläche unter der Verteilungsfunktion bis zum Target darstellen. Mit dem LPM2 wird die so genannte Downside-Varianz beschrieben. Durch die Quadrierung der Zielverfehlungen werden dabei sehr niedrige Renditen stärker gewichtet als Renditen knapp unterhalb des Targets (Meyer, C. 1999). Welchen Wert die Zielrendite T einnehmen sollte, hängt vom individuellen Risikoverständnis des Entscheiders ab. Eine Zielrendite von 0% ist beispielsweise sinnvoll, falls sich für den Investor das Risiko einer Anlage in der Minderung des (Nominal-) Wertes ausdrückt. Werden die Rendite einer alternativen risikolosen Anlage oder die erwartete Rendite eines Marktindex als Target herangezogen, dann spiegelt sich der Opportunitätsgedanke im Risikobegriff wider. Diese von der Renditeverteilung unabhängigen Targets erlauben es, das Risiko verschiedener Investitionsalternativen mithilfe der Lower Partial Moments miteinander zu vergleichen. Es können aber auch von der jeweiligen Verteilung abhängige Targets gewählt werden, z.B. der Erwartungswert. Der LPM2 entspricht in diesem Fall der oben definierten Semivarianz (i.e.S.). In jedem Fall gilt, dass je höher die ausgewählte Zielrendite ist, desto höher sind c.p. die Lower Partial Moments (Portmann, T. 1999).
Der für ein bestimmtes Target berechnete LPM1 ist grundsätzlich mit der stochastischen Dominanz zweiten Grades vereinbar. Ein risikoaverser Entscheider, der seinen Erwartungsnutzen maximiert, würde sich folglich auf der Grundlage des LPM1 nicht anders entscheiden als auf Basis der stochastischen Dominanz zweiten Grades. Dieser Zusammenhang gilt zwingend nur, falls eine Risikoanordnung mittels der stochastischen Dominanz zweiter Ordnung möglich ist und die Verteilungsfunktionen der beiden zu vergleichenden Investitionsmöglichkeiten für die betrachtete Zielrendite nicht denselben Wert annehmen (Guthoff, A./Pfingsten, A./Wolf, J. 1998). c) Value-at-Risk
Das z. Zt. am häufigsten diskutierte Risikomaß ist der Value-at-Risk. Er gibt den maximalen Verlust (die maximale Verlustrendite) an, der innerhalb eines bestimmten Zeitraums mit einer gewissen Wahrscheinlichkeit (Konfidenzniveau 1-α) nicht überschritten wird. Mithilfe der Abb. 1 soll die Verwandtschaft mit dem LPM0 verdeutlicht werden. 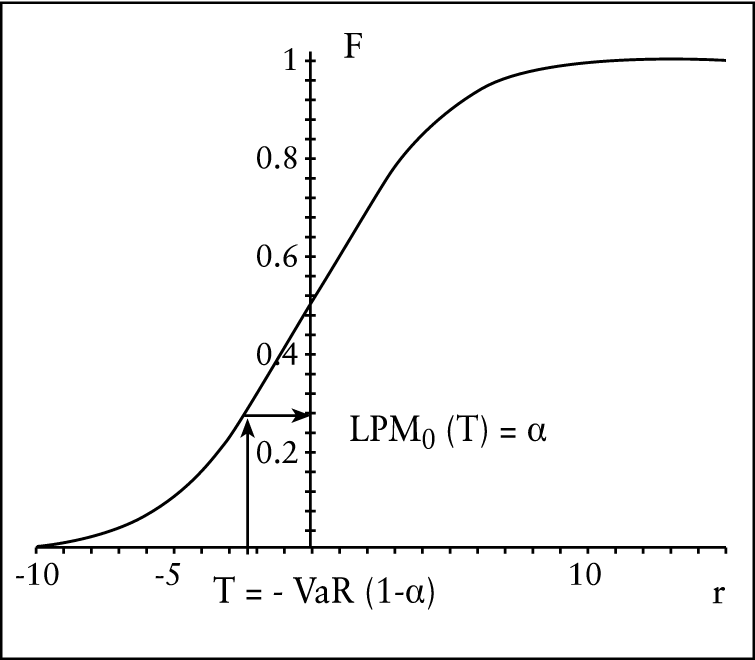
Abb. 1.: Zusammenhang zwischen LPM0 und Value-at-Risk (VaR)
Während der LPM0 als Downside-Wahrscheinlichkeit die Wahrscheinlichkeit eines Unterschreitens des Targets angibt, entspricht der Value-at-Risk bei einem Konfidenzniveau von 1-α = 1-LPM0(T) dem Absolutwert des (negativen) Targets:
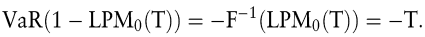
LPM0 und VaR können also grundsätzlich ineinander überführt werden. Johanning weist jedoch nach, dass beide Risikomaße (für eine bestimmte Downside-Wahrscheinlichkeit bzw. ein bestimmtes Target) nicht zwingend zu einer identischen Anordnung von Verteilungen führen (Johanning, 1998, S. 246ff.)
Ein wesentlicher Vorteil des VaR als Risikomaß ist seine Anschaulichkeit. Von den vielen Kritikpunkten sei hier nur darauf hingewiesen, dass eine Risikoanordnung nach dem Value at Risk der Risikoanordnung nach der stochastischen Dominanz zweiter Ordnung widersprechen kann. Anlageentscheidungen auf Basis des Erwartungswertes und des Value-at-Risk führen nicht zwangsläufig zur Erwartungsnutzenmaximierung (Guthoff, A./Pfingsten, A./Wolf, J. 1998).
In Erweiterung des Value-at-Risk-Konzeptes wird – basierend auf dem LPM1 – ein so genannter Shortfall-Value-at-Risk vorgeschlagen (Portmann, T. 1999). Bezogen auf eine Renditeverteilung ergibt sich der Shortfall-VaR als
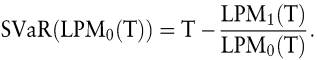
Für eine vorgegebene Downside-Wahrscheinlichkeit LPM0 lässt sich mit T = F – 1(LPM0) die Zielrendite (und damit auch der Value-at-Risk) berechnen. Der für dieses Target berechnete Downside-Erwartungswert LPM1 wird standardisiert mittels Division durch LPM0 und vom Target subtrahiert. Der so ermittelte Shortfall-VaR stellt ein Maß für die zu erwartende Rendite dar, falls der Value-at-Risk unterschritten wird. Damit wird der Mangel des Value-at-Risk (und des LPM0) behoben, dass die Höhe und die Wahrscheinlichkeit der Überschreitungen des Value-at-Risk nicht betrachtet werden.
III. Analogien zwischen Risikomaßen und Ungleichheits- bzw. Armutsmaßen
1. Gesamtrisikomaße und Ungleichheitsmaße
Rothschild/Stiglitz haben drei äquivalente Definitionen dafür präsentiert, dass eine Zufallsvariable X weniger riskant als eine Zufallsvariable Y ist (Rothschild, M./Stiglitz, J. E. 1970):
| 1. | Die Zufallsvariable Y entsteht aus X, indem eine unkorrelierte Zufallsvariable mit Erwartungswert null hinzugefügt wird. | | 2. | Wenn X und Y denselben Mittelwert haben, zieht jeder Erwartungsnutzenmaximierer mit einer monoton wachsenden und konkaven Nutzenfunktion X gegenüber Y vor. | | 3. | Die Zufallsvariable Y entsteht aus X, indem bei gleich bleibendem Mittelwert mehr Gewicht auf die „ Ränder “ der Verteilung geschoben wird. |
Die letztgenannte Definition, die das Konzept eines Mean Preserving Spread verwendet, beinhaltet im Wesentlichen die gleiche Vorstellung, die in der Verteilungstheorie zur Ordnung von Einkommensverteilungen nach ihrer Ungleichheit verwendet wird. Dort ist es gängig (Bossert, /Pfingsten, 1990), von Ungleichheitsmaßen die Gültigkeit des Prinzips des progressiven Transfers von Dalton zu verlangen. Es besagt, dass die Ungleichheit in einer Einkommensverteilung abnimmt, wenn ein Reicherer einem Ärmeren einen Einkommensbetrag abgibt, der höchstens die Hälfte ihrer bisherigen Einkommensdifferenz ausmacht.
Ökonomische Kennzahlen, die das Transferprinzip erfüllen, sind insofern auch als Risikomaße geeignet. Die Analogie zwischen Ungleichheit und Gesamtrisiko kann mit einem Bild von Pen sehr schön verdeutlicht werden (Pen, J. 1971). Zur Darstellung der Einkommensverteilung stellt er sich vor, dass alle Menschen in ihrer Größe so skaliert werden, dass die Größe eine lineare Funktion des Einkommens ist. Dann werden die Menschen der Größe nach aufgestellt und gehen anschließend in einer „ Einkommensparade “ am Beobachter vorüber – eine beeindruckende Kette vieler Zwerge und einiger weniger Riesen. In der Gesamtrisikomessung entspricht eine Person ungefähr einem möglichen auftretenden Ereignis und das Einkommen beispielsweise einer bestimmten Renditerealisation. Bei der bloßen Messung von Ungleichheit kommt es nicht darauf an, zu wissen, welche Person ein bestimmtes Einkommen hat. Entsprechend ist es bei der Messung des Gesamtrisikos unerheblich, bei welchem Ereignis eine bestimmte Rendite erzielt wird. Durch die Verwendung von Verteilungsfunktionen für Einkommen oder Renditen gehen daher diesbezüglich keine Informationen verloren. Erst in einem späteren Stadium, wenn es um Maßnahmen der Ungleichheits- bzw. um solche der Gesamtrisikoreduzierung geht, ist es wichtig, die einzelnen Personen oder Ereignisse genau charakterisieren zu können.
Vor diesem Hintergrund überrascht es zunächst, dass die Standardabweichung der Einkommen durchaus gelegentlich zur Beurteilung der Einkommensungleichheit verwendet wird, hingegen die Verwendung des Gini-Index, eines wichtigen Ungleichheitsmaßes, in der Gesamtrisikomessung kaum vorkommt. Dafür können neben der Unkenntnis über die prinzipielle Übertragbarkeit von Kennzahlen spezielle Eigenschaften der beiden Maße verantwortlich sein, die in den beiden Problemkreisen von unterschiedlicher Relevanz oder Wünschbarkeit sind.
2. Downside-Risikomaße und Armutsmaße
Gesamtrisikomaße verfolgen die statistische Erfassung der gesamten zugrunde liegenden Renditeverteilung und weisen deshalb die oben beschriebene Analogie zu Ungleichheitsmaßen auf. Im Unterschied hierzu beschreiben Downside-Risikomaße nur einen bestimmten unteren Teil einer Renditeverteilung, konzentrieren sich also beispielsweise auf die Verfehlung einer angestrebten Zielrendite. Auch hierzu gibt es mit den Armutsmaßen ein Analogon aus der Wohlfahrtsökonomik, da diese nur die Einkommen am unteren Ende einer Einkommensverteilung, d.h. unterhalb einer zumeist exogen vorgegeben Armutsgrenze, berücksichtigen.
Entsprechend der Quantifizierung von Gesamtrisiko bzw. Ungleichheit ist es bei der Messung von Downside-Risiko bzw. Armut nicht notwendig zu wissen, bei welchem Ereignis eine bestimmte Rendite erzielt wird bzw. welche Person ein bestimmtes Einkommen hat, sodass auch hier Verteilungsfunktionen ohne Informationsverlust verwendet werden können. Gleichwohl sind bei der Übertragung von Konzepten der Armutsmessung in die Downside-Risikomessung einige formale Klippen zu beachten, die eine Anpassung der in der Armutsmessung verwendeten Maßzahlen notwendig machen. Zum einen wird in der Wohlfahrtsökonomik häufig mit diskreten Verteilungen gearbeitet, wohingegen kapitalmarkttheoretischen Modellen oftmals stetige Verteilungen zugrunde liegen. Zum anderen kann es bei Renditeverteilungen zu negativen Realisationen kommen, während bei Einkommensverteilungen üblicherweise Nicht-Negativität der Realisationen unterstellt wird.
Beispielhaft lässt sich die Übertragung eines Armutsmaßes in ein Downside-Risikomaß anhand des Sen-Index verdeutlichen. Hat der aus der Armutsmessung bekannte Sen-Index (Sen, A. 1976) die Form S = H [I + (1 + I) · G], so führt seine Übertragung in die Downside-Risikomessung (Eggers, F./Pfingsten, A./Rieso, S. 1999) zu folgender Neuformulierung
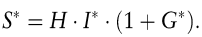
Die Besonderheit dieses auf die Downside-Risikomessung übertragenen Sen-Index ist darin zu sehen, dass er zur Quantifizierung der verschiedenen Dimensionen von Downside-Risiko mehrere Komponenten miteinander verknüpft, die im Vergleich zum ursprünglichen Sen-Index teilweise modifiziert werden müssen und eine unterschiedlich stark ausgeprägte Ähnlichkeit zu bereits bekannten Downside- und Gesamtrisikomaßen aufweisen. So entspricht H dem LPM0 und misst die Wahrscheinlichkeit der Verfehlung der vorgegebenen Zielrendite. I* quantifiziert als Yield-Gap-Ratio den prozentualen Anteil der erwarteten Zielverfehlung an der maximal möglichen Verfehlung bei gegebenem H. Strukturell ähnelt es als Kennzahl für das durchschnittliche Ausmaß der Verfehlungen daher dem LPM1. G* bringt als auf den Downside-Bereich normalisierter Gini-Index die Verteilungsungleichheit bzw. Streuung der Renditen unterhalb der Zielrendite zum Ausdruck. Insoweit besteht in der gemeinsamen Charakterisierbarkeit als Streuungsmaß eine Verbindung zur Varianz bzw. zur Standardabweichung. Zu beachten sind allerdings die konzeptionellen Unterschiede von Gini-Index und Varianz bzw. Standardabweichung hinsichtlich der Quantifizierung des Streuungsausmaßes.
Beim Vergleich zweier Renditeverteilungen anhand des Sen-Index ist zu beachten, dass nicht zwingend sämtliche in ihm erfasste Dimensionen des Downside-Risikos für sich allein genommen dieselbe Verteilung als die riskantere ausweisen werden. Deshalb kann eine auf Basis des Sen-Index oder eines anderen aggregierten Index ermittelte Rangordnung von Renditeverteilungen nicht ohne Kenntnis der hinter dieser Aggregation stehenden Präferenzordnung übernommen werden. Bereits aus Arrows Unmöglichkeitstheorem (Arrow, K. J. 1963) ist nämlich bekannt, dass es nicht zweifelsfrei möglich ist, eine unkontroverse Aggregation vorzunehmen; denn eine Aggregation beinhaltet letztlich immer eine nicht präferenzfreie Gewichtung der einzelnen Dimensionen.
Über den Transfer von Armutsmaßen in Downside-Risikomaße hinaus ermöglicht die formale Analogie zwischen Armuts- und Downside-Risikomessung die Ableitung eines Kataloges von Axiomen, der bestimmte wünschenswerte Eigenschaften eines „ guten “ Downside-Risikomaßes formuliert. Dieses geschieht einerseits durch die Anpassung der aus der Armutsmessung bereits bekannten Axiome an die formalen Unterschiede zwischen Armuts- und Downside-Risikomessung; andererseits werden mithilfe ökonomischer Überlegungen neue Axiome entwickelt (Breitmeyer, C./Hakenes, H./Pfingsten, A. et al. et. al.1999).
Literatur:
Arrow, K. J. : Social Choice and Individual Values, New York 1963
Bossert, /Pfingsten, : Intermediate Inequality, in: Mathematical Social Sciences 1990, S. 117 – 134
Brachinger, H. W./Weber, M. : Risk as a Primitive, in: ORSp 1997, S. 235 – 250
Breitmeyer, C./Hakenes, H./Pfingsten, A. et al. : Learning From Poverty Measurement, Diskussionsbeitrag 99 – 03, hrsg. v. Institut für Kreditwesen, Münster 1999
Copeland, T. E./Weston, J. F. : Financial Theory and Corporate Policy, 3. A., Reading et al. 1988
Eggers, F./Pfingsten, A./Rieso, S. : Three Dimensions of Shortfall Risk, Diskussionsbeitrag 99 – 04, hrsg. v. Institut für Kreditwesen, Münster 1999
Franke, G./Hax, H. : Finanzwirtschaft des Unternehmens und Kapitalmarkt, 4. A., Berlin et al. 1999
Guthoff, A./Pfingsten, A./Wolf, J. : Der Einfluß einer Begrenzung des Value at Risk oder des Lower Partial Moment One auf die Risikoübernahme, in: Credit Risk und Value-at-Risk Alternativen, hrsg. v. Oehler, A., Stuttgart 1998, S. 111 – 153
Hadar, J./Russell, W. R. : Rules for Ordering Uncertain Prospects, in: AER 1969, S. 25 – 34
Hadar, J./Russell, W. R. : Stochastic Dominance and Diversification, in: JETheory 1971, S. 288 – 305
Hanoch, G./Levy, H. : The Efficiency Analysis of Choices Involving Risk, in: REStud. 1969, S. 335 – 346
Hartmann-Wendels, T./Pfingsten, A./Weber, M. : Bankbetriebslehre, 2. A., Berlin et al. 2000
Hartung, J./Elpelt, B./Klösener, K.-H. : Statistik, 12. A., München et al. 1999
Johanning, L. : Value at Risk zur Marktrisikosteuerung und Eigenkapitalallokation, Bad Soden et al. 1998
Kaduff, J. V./Spremann, K. : Sicherheit und Diversifikation bei Shortfall-Risk, in: ZfbF 1996, S. 779 – 802
Kreyszig, E. : Statistische Methoden und ihre Anwendungen, 7. A., Göttingen 1979
Kruschwitz, L. : Finanzierung und Investition, 2. A., München et al. 1999
Markowitz, H. M. : Portfolio Selection, in: JoF 1952, S. 77 – 91
Markowitz, H. M. : Portfolio Selection, 2. A., Cambridge et al. 1991
Meyer, C. : Value at Risk für Kreditinstitute, Wiesbaden 1999
Mülhaupt, L. : Einführung in die Betriebswirtschaftslehre der Banken, 3. A., Wiesbaden 1980
Pen, J. : Income Distribution, Harmondsworth 1971
Portmann, T. : Zeithorizontverhalten von Lower Partial Moments, Bern et al. 1999
Rothschild, M./Stiglitz, J. E. : Increasing Risk I: A Definition, in: JETheory 1970, S. 225 – 243
Roy, A.D. : Safety First and the Holding of Assets, in: ENM 1952, S. 431 – 449
Sachs, L. : Angewandte Statistik, 8. A., Berlin et al. 1997
Sarin, R. K./Weber, M. : Risk-Value Models, in: European Journal of Operational Research 1993, S. 135 – 149
Schmidt, R. H./Terberger, E. : Grundzüge der Investitions- und Finanzierungstheorie, 4. A., Wiesbaden 1997
Sen, A. : Poverty: An Ordinal Approach to Measurement, in: ENM 1976, S. 219 – 231
Serf, B. : Portfolio Selection auf der Grundlage symmetrischer und asymmetrischer Risikomaße, Frankfurt a.M. et al. 1995
Steiner, M./Bruns, C. : Wertpapiermanagement, 7. A., Stuttgart 2000
Weber, M. : Risikoentscheidungskalküle in der Finanzierungstheorie, Stuttgart 1990
|