|
Kausalanalyse
Inhaltsübersicht
I. Das Prinzip der Kausalanalyse
II. Der LISREL-Ansatz
III. Kausalmodelle im Marketing
IV. Probleme der Kausalanalyse
I. Das Prinzip der Kausalanalyse
Der Gehalt marketingwissenschaftlicher Aussagen hängt in hohem Maße davon ab, ob bei der empirischen Prüfung theoretischer Modelle die wesentlichen Einflussgrößen erfasst worden sind und potenzielle Fehlereinflüsse kontrolliert werden. Dies gilt insbesondere für die verhaltenstheoretischen Modelle und Theorien des Marketing, deren Basis die Beziehung zwischen theoretischen Konstrukten wie z.B. Image, Einstellung oder Commitment ist. Bei jedem Modelltest hat der Forscher hier zunächst ein Mess- und Validierungsproblem zu lösen, das üblicherweise dem Hypothesentest vorgelagert ist.
Eine \'ganzheitliche\' Vorgehensweise zur Validierung und zum Test von Theorien bieten die Methoden der \'Kausalanalyse\'. Sie stehen für einen Ansatz der Multivariatenanalyse, der je nach Formalisierung auch als Kovarianzstrukturanalyse, Strukturgleichungs- oder LISREL-Methodologie bezeichnet wird. Ausgangspunkt der Kausalanalyse sind im Allgemeinen die Varianzen und Kovarianzen experimenteller oder nicht experimenteller Daten, anhand derer eine theoretische Struktur, formalisiert als lineares Gleichungssystem, getestet wird. Charakteristisch für die Modelle der Kausalanalyse ist die Integration von Faktorenanalyse und Regressionsanalyse und die Möglichkeit einer simultanen Schätzung beider Modellbereiche. Je nach Art der theoretischen Grundlage kann durch die Faktorstruktur in einem spezifizierten Modell explizit zwischen beobachteten Variablen und theoretischen Variablen (den Konstrukten) sowie Messtheorie und Substanztheorie unterschieden werden. Die Kausalanalyse ermöglicht dann:
| 1. | den Test eines kausalen oder funktionalen Netzwerks von Beziehungen zwischen Variablen und/oder Konstrukten (Faktoren), | | 2. | die Kontrolle von Messfehlern und die Validierung der Messungen theoretischer Konstrukte in einem Faktormodell, | | 3. | die Zerlegung von kausalen Einflüssen in direkte und indirekte Wirkungen. |
Ein einfaches Kausalmodell mit zwei Kausalhypothesen (ξ1η1 und ξ2η1) und drei Messhypothesen (als Faktormodelle) (z.B. ξ1→x1) ist in Abb. 1 dargestellt. Die zugrunde liegenden Hypothesen werden durch das Pfaddiagramm und die Gleichungssysteme repräsentiert, die Symbolik ist vom LISREL-Ansatz übernommen. Das Modell für die Substanz- bzw. Kausaltheorie wird im Allgemeinen als Strukturmodell bezeichnet.
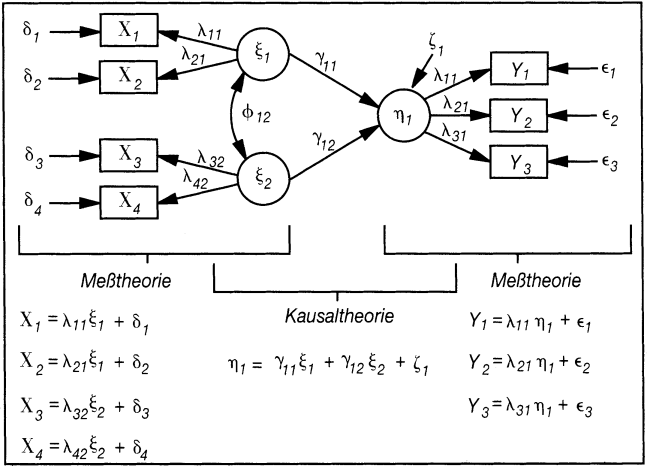
Abb. 1: Die Struktur eines Kausalmodells
Das Strukturmodell kann auch mehrere abhängige (endogene) Konstrukte (η) berücksichtigen, zwischen denen dann wieder kausale Beziehungen spezifiziert werden können.
Die Konzeption der Kausalanalyse kann als Analogie zu wissenschaftstheoretischen Konzepten von Hempel und Carnap (Carnap, R. 1966) aufgefasst werden, die zwischen empirischer Sprache (Ebene der Beobachtungsvariablen) und theoretischer Sprache (Ebene der Konstrukte) unterscheiden. Bagozzi sieht deshalb in der Kausalanalyse auch den einzigen Ansatz, der den wissenschaftstheoretischen Anforderungen einer Prüfung sozialwissenschaftlicher Hypothesen genügt. Er bezieht sich dabei auf die Möglichkeit der ganzheitlichen Vorgehensweise beim Theorietest (Bagozzi, R. P. 1998).
Die Theorieprüfung mit der Kausalanalyse hat paradigmatischen Charakter für die Vorgehensweise bei der empirisch-quantitativen Forschung im Marketing. Dieser Ansatz beruht darauf, bei Forschungsaufgaben zunächst (Mess- und Kausal-)Hypothesen – in Form von »wenn – dann« oder „ je – desto« Aussagen – zu entwickeln und die verbal formulierte \'Theorie\' in ein Pfaddiagramm zu übersetzen (das \'Kausalmodell\'). Dieses muss die Richtung der angenommenen Beziehungen zwischen den Variablen der Beobachtungsebene und den Konstrukten der zugrunde liegenden Theorie widerspiegeln. Das Pfaddiagramm wird dann in ein Gleichungssystem überführt, dessen Parameterstruktur anhand von empirischen Daten zu testen ist. Bei diesem Test werden die Varianzen und Kovarianzen der empirischen Daten auf ihre Konsistenz mit der Kovarianzstruktur des geschätzten theoretischen Kausalmodells geprüft. Bei fehlender Konsistenz ist die Theorie zu verwerfen.
Die Durchführung von Kausalanalysen im Marketing war lange Zeit fast ausschließlich mit der Anwendung des Programms LISREL von Jöreskog und Sörbom verbunden (Jöreskog, K. G./Sörbom, D. 1996a). Mittlerweile existiert eine Reihe von weiteren Programmsystemen, die alternativ zu LISREL eingesetzt werden können (zu einem Überblick siehe Hildebrandt, L. 2004). Im Rahmen weit verbreiteter Statistiksoftware werden die Programme AMOS (Arbuckle, J. L. 2005; SPSS), CALIS (Hartmann, W. M. 1992; SAS), RAMONA (Browne, M./Mels, G./Cowan, M. 1994; SYSTAT) und SEPATH (Steiger, J. 1995; STATISTICA) angeboten. Daneben existieren ausschließlich als Stand-alone-Versionen verfügbare Programme wie z.B. EQS (Bentler, P. M./Wu, E.J. C. 2002) oder Mplus (Muthén, B. O./Muthén, L. K. 1998 – 2006). Zusätzlich zur kommerziellen Software kann für die Schätzung von Strukturgleichungsmodellen auch auf kostenlose Programme zurückgegriffen werden. So ist z.B. unter dem Open-Source-Statistikprogramm R das Paket „ sem “ verfügbar, das auf dem RAM-Ansatz (McArdle, J. J./McDonald, R. P. 1984) beruht; von Neale (Neale, et al. 2003) wird das Programm Mx angeboten.
Neben der in vielen sozialwissenschaftlichen Disziplinen populären Kovarianzstrukturanalyse ist in der letzten Zeit eine gewisse Renaissance des Partial-Least-Squares (PLS)-Ansatzes festzustellen. Die Zielsetzung dieser Methodik besteht nicht in der möglichst guten Anpassung eines Modells an die empirische Kovarianzmatrix, sondern in der Maximierung der erklärten Varianz der Modellvariablen. Programme wie PLS-Graph (Chin, W. W. 2001) und SmartPLS (Hansmann, K.-W./Ringle, C. M. 2004) zeichnen sich gegenüber der ersten verfügbaren PLS-Software LVPLS (Lohmöller, J-B. 1984) insbesondere durch die stark verbesserte Benutzerfreundlichkeit aus (Temme, D./Kreis, H. 2005).
Die Programme zur Schätzung von Kovarianz-Strukturmodellen unterscheiden sich in erster Linie in der Art der Spezifikation der zu testenden Modellstruktur, des Schätzalgorithmus und des Benutzerkomforts der Programmsteuerung. Aufgrund der großen Akzeptanz sollen aber in diesem Beitrag Nomenklatur und Struktur des LISREL-Ansatzes genauer dargestellt werden.
II. Der LISREL-Ansatz
LISREL (Analyse von Linear Structural Relationships) liegt zurzeit in der achten Programm-Version vor und beruht im Kern auf einer Ineinanderschachtelung von Faktoranalyse-Modellen. Deren Parameter können nach einer groben Startwertbestimmung (sog. IE-Schätzer) mit Maximum Likelihood (ML) oder Kleinste-Quadrate Methoden (ULS, GLS) geschätzt werden. Eine Kovarianzmatrix von Daten wird als Funktion von Parametern eines theoretischen linearen Modells aufgefasst, das die verschiedenartigen Beziehungen zwischen Beobachtungsvariablen, Faktoren und Fehlerkomponenten gleichzeitig abbildet. Die Faktoren repräsentieren die nicht direkt beobachtbaren Konstrukte oder latenten Variablen, die Faktormodelle die \'Messtheorie\'. Die Beziehungen zwischen den Faktoren bilden die substanzielle Theoriestruktur.
Ein LISREL-Kausalmodell besteht dann aus drei Modellteilen, einem exogenen Messmodell, einem endogenen Messmodell und einem Strukturgleichungsmodell (Abb. 1).
Nach den Konventionen von LISREL 8 wird angenommen, dass alle Variablen als Abweichungen vom Mittelwert gemessen sind. Dadurch entfallen die Absolutglieder in den Gleichungen. Für den Ein-Sample-Fall hat das Modell dann folgende Struktur:
Die Variablen werden unterschieden nach Messungen x\' = (x1, x2, ?, xp) von unabhängigen (exogenen) Konstrukten ξ\' = (ξ1, ξ2, ?, ξn,) und Messungen y\' = (y1, y2, ? yq) von abhängigen (endogenen) Konstrukten η\' = (η1, η2, ?, ηm). Durch zwei Faktormodelle
x = Λxξ + δ (1)
y = Λyη + ε (2)
werden die Beziehungen zwischen den Beobachtungsvariablen (x, y) und den Konstrukten (ξ, η) abgebildet. e und d sind die Vektoren der Messfehler von y und x. Die Matrizen Λy (q×m) und Λx (p×n) erfassen die Faktorladungen (Regressionsgewichte) von y auf η sowie x auf ξ. Die kausalen Beziehungen werden dann durch ein System von linearen Strukturgleichungen auf der Konstruktebene modelliert:
η = Bη + Gξ + ζ oder B?ηη = Γξ + ζ (3)
mit [B? = (I – B)]; hier ist B die (m×n) Koeffizientenmatrix für die direkten kausalen Beziehungen zwischen endogenen Konstrukten η, und Γ die (m×n) Koeffizientenmatrix für die direkten kausalen Beziehungen zwischen den exogenen Konstrukten ξ und den endogenen Konstrukten η. ζ\' = (ζ1, ζ2 ?, ζm) ist der Zufallsvektor von Residuen in den Kausalbeziehungen.
Zur Lösbarkeit der Gleichungssysteme werden folgende Basisannahmen getroffen: ε und δ sind untereinander unkorreliert und unkorreliert mit η, ξ und ζ. ζ ist unkorreliert mit den exogenen Konstrukten ξ, und die Matrix I – B ist nicht singulär.
Das Programm schätzt Parameter unter Berücksichtigung von Restriktionen und Parametervorgaben in acht Parametermatrizen, die eine vollständige Modellstruktur abbilden. Dies sind neben den Abhängigkeitsbeziehungen in Λx, Λy, B, Γ die spezifizierten Kovariationsbeziehungen in:
Φ der (n×n) Varianz-Kovarianzmatrix der exogenen Konstrukte,
Ψ der (m×m) Varianz-Kovarianzmatrix der Fehler ζ in den Strukturgleichungen,
Θδ, Θε den (p×p), (q×q) Varianz-Kovarianzmatrizen der Fehler δ, ε in den Faktormodellen
Sofern die Information in den Daten ausreicht, um alle Koeffizienten eindeutig zu bestimmen, d.h. das Modell identifiziert ist, können je nach Qualität der Daten unterschiedliche Methoden zur Schätzung der Parameter eingesetzt werden. Die ML-Methode verlangt formal multivariat-normalverteilte Variablen, während die ULS- und GLS-Schätzmethoden weniger restriktiv sind. Zur Überprüfung der Verteilungsannahmen kann der Nutzer auf Zusatzmodule (z.B. PRELIS) zugreifen (Jöreskog, K. G./Sörbom, D. 1996b).
Das Schätzproblem der ML-Schätzung in LISREL besteht darin, über den Parametervektor π (d.h. die unbekannten Parameter der acht LISREL-Matrizen) die modellimplizierte Kovarianzmatrix S zu schätzen, die mit größter Wahrscheinlichkeit die empirische Kovarianzmatrix der Daten S erzeugt hat. Bei Annahme einer Wishartverteilung von S erfolgt die Schätzung über die iterative Minimierung der Funktion
F(π) = log|Σ| + tr(SΣ-1) – log|S| – (p + q), (4)
wobei tr die Spur einer Matrix angibt. Die Schätzung über ULS minimiert die Funktion
F(π) = 1/2 tr[(S – Σ)2] (5)
Gemeinsam ist allen Schätzmethoden, dass sie die Abweichung der Gesamtheit der Werte der empirischen Kovarianzen von den durch das Modell reproduzierten Werten minimieren. Sind die theoretisch postulierten Beziehungen, d.h. die geschätzten Varianzen-Kovarianzen konsistent mit den empirischen Daten, dann wird die zugrunde liegende Theorie als nicht falsifiziert betrachtet bzw. zu dem Grad akzeptiert, zu dem das Modell nicht an den Daten scheitert. Zur Beurteilung der Modellanpassung liefert LISREL dem Benutzer Fit-Indices und Teststatistiken zur Beurteilung der Gesamtstruktur sowie von Teilstrukturen. Am gebräuchlichsten sind GFI, AGFI, Tucker/Lewis\' NNFI und Bentler/Bonett\'s NFI, deren Werte nahe 1 liegen sollten sowie der RMSEA, dessen Wert kleiner 0,06 sein sollte (Bollen, K. A. 1989; Hu, L. T./Bentler, P. M. 1999).
Zur Gesamtmodellprüfung kann im Fall der ML- oder GLS-Schätzung als strengste Instanz ein Chi2-Test eingesetzt werden. LISREL berechnet dabei einen modellspezifischen Wahrscheinlichkeitswert p für den Fehler erster Art (Ablehnung des richtigen Modells). p sollte größer als eine Signifikanzschwelle von α = ,10 sein. Die Teststatistik ist nur valide bei normalverteilten Daten, der Analyse von Kovarianzmatrizen und angemessen großen Stichproben (≈ 400). Die Schätzung einer Gütefunktion kann über Hilfsverfahren erfolgen (Satorra, A./Saris, W. E. 1985). Ansonsten sollte die Statistik als Fit-Index interpretiert oder zur Beurteilung alternativer Modellhypothesen als Chi2-Differenztest eingesetzt werden.
Für explorative Studien liegt in LISREL ein Modifikationsindex vor, der angibt, um wie viel sich die Chi2-Teststatistik verbessert, wird ein beliebiger restringierter Parameter geschätzt (zur explorativen Modellanpassung Homburg, C. 1989).
Problematisch bei der Anwendung des Chi2-Tests ist seine Sensitivität gegenüber der Stichprobengröße. Deshalb ist es ratsam, mehrere sich ergänzende Fit-Indices je nach Stichprobengröße, Datenqualität oder Schätzprozedur nebeneinander zur Modellevaluation zu verwenden. LISREL bietet mehr als 25 unterschiedliche Prüfkriterien. Die Fit-Indices, Angaben über die Standardfehler der Parameter und Residualvarianzen in einzelnen Faktor- und Regressionsstrukturen lassen in der Summe eine verlässliche Aussage über die Validität eines geschätzten Modells zu.
Das allgemeine LISREL-Modell kann flexibel zur Spezifikation und zum Test vieler Modelltypen eingesetzt werden, z.B. für Pfadmodelle, Modelle der konfirmatorischen Faktorenanalyse, zweistufige Faktormodelle, Kausalmodelle, für die Ein- und Mehrgruppenanalyse, Zeitreihen- und Panelanalysen mit autokorrelierten Residuen, Modelle für höhere Produktmomente und Modelle zum Test von Mittelwertstrukturen auf der Ebene der Faktoren. Auf die Parameter können lineare und nicht-lineare Beschränkungen gelegt werden. Der Nutzer kann Intervallrestriktionen vorgeben. Er kann bei der Modellspezifikation auch von der vorgegebenen Struktur des LISREL-Modells (Abb. 1) abweichen und jede beliebige Kovarianzstruktur schätzen.
Bei der Programm-Version LISREL 8 ist mit der SIMPLIS-Kommandosprache eine Steuerung des Programms ohne umfangreiche Kenntnisse der Matrixalgebra möglich.
III. Kausalmodelle im Marketing
Im Marketing hat die Kausalanalyse besonders durch die Berücksichtigung verhaltenswissenschaftlicher Erkenntnisse in Teilbereichen der Forschung Beachtung gefunden, in denen die Voraussetzung der experimentellen Prüfung kausaler Beziehungen nur unvollkommen herzustellen ist. Typische Anwendungsfelder sind Bereiche, in denen der Forscher eine Vielzahl von Einflüssen durch vernetzte Hypothesen zu berücksichtigen hat und objektspezifische Operationalisierungsprobleme auftreten. Hierzu gehören Studien der Einstellungs-Verhaltens-Forschung, der Produkt-Zufriedenheitsforschung sowie der Image- und Involvementforschung (Trommsdorff, V. 1989).
In anderen Bereichen findet die Kausalanalyse ihre Anwendung, wenn Befragungsdaten und Indikatoren für die Prüfung von Hypothesen vorliegen. So werden besonders in den Studien zur Erfolgsfaktorenforschung kausalanalytische Methoden eingesetzt (Annacker, D. 2001; Fritz, W. 1992; Hildebrandt, L. 1992).
Reliabilitätsprüfung, kausalanalytische Validierung und der Test von Kausalbeziehungen mit Messfehlerkontrolle können als dominierende Aufgaben der Kausalanalyse im Marketing angesehen werden. Die Reliabilitätsprüfung (z.B. nach Cronbach\'s α) beruht auf dem Test der Eindimensionalität einer Itembatterie mit einem Faktormodell
x = Λxξ + δ (6)
Das Faktormodell gibt über die Schätzwerte der λi und den Varianzen der Fehlerterme di die Möglichkeit, die Reliabilität jedes Items zu berechnen. Allgemein definiert ist die Reliabilität als die quadratische Korrelation zwischen dem Konstrukt auf seinen Messungen. Im Modell lassen sich einzelne und zusammengesetzte Reliabilitätsmaße berechnen, wobei nachfolgend angenommen wird, dass die Varianzen der Konstrukte auf eins standardisiert sind. Die Reliabilität der einzelnen Items ergibt sich dann über
ρi = (Λi2) / (Λi2 + Θii) (7)
mit Θii, der Fehlervarianz und ρi, der Indikator-Reliabilität. Als zusammengesetztes Maß für alle Items im Faktormodell eines Konstruktes wird die Faktor-Reliabilität über Summen berechnet mit
ρc = (Σλi)2 / (Σλi)2 + ΣΘii) (8)
Beide Indices haben einen Wertebereich zwischen 0 und 1, je größer ρ, desto größer die Reliabilität. Für erweiterte Tests sei auf Bagozzi (Bagozzi, R. P. 1980) verwiesen.
Die kausalanalytische Validierung beruht auf dem Konzept der Validitätsprüfung mit der MTMM (Multitrait-Multimethod-)Matrix von Campbell und Fiske.
Diese wird gebildet aus den Messungen verschiedener Konstrukte mit jeweils mehreren Messinstrumenten, die maximal unterschiedlich sein sollen. Mit einem Modell der konfirmatorischen Faktorenanalyse lässt sich dann prüfen, ob die Kriterien der MTMM-Validierung: Konvergenzvalidität als Grad, zu dem mehrere Messungen mit verschiedenen unabhängigen Messmethoden übereinstimmen und Diskriminanzvalidität als Grad, zu dem sich die Messungen mit gleichen Messmodellen unterscheiden, erfüllt sind (Campbell, D. T./Fiske, J. D. 1959).
Das Pfadmodell der konfirmatorischen Faktorenanalyse für die Prüfung von Konvergenz- und Diskriminanzvalidität ist in Abb. 2 dargestellt.
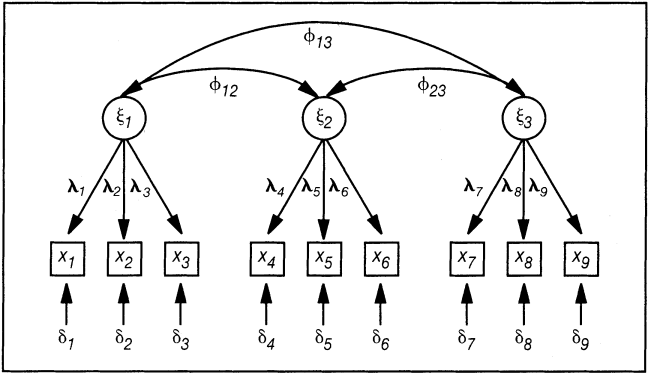
Abb. 2: Das Modell der konfirmatorischen Faktorenanalyse zur Prüfung von Konvergenz- und Diskriminanzvalidität
Das Modell berücksichtigt drei Faktoren mit jeweils drei Messungen. Die Validitätskriterien lassen sich über einen hierarchischen Modelltest (über Parameterstrukturen und Modell-Fit) prüfen mit den Hypothesen in Tab. 1.
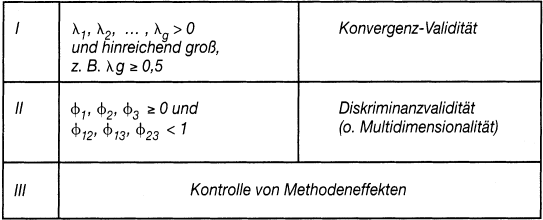
Tab. 1: Validitätstest mit der konfirmatorischen Faktorenanalyse
Das dargestellte Modell wird auch als »Trait-only«-Modell bezeichnet und geht davon aus, dass keine Methodeneffekte vorliegen. Der Test dieser Effekte kann über die Einführung weiterer Faktoren oder die Schätzung von Messfehlerkorrelationen bei gleichen Messmodellen erfolgen (Hildebrandt, L. 1998). Allerdings hat eine Meta-Analyse von Validierungen mit der konfirmatorischen Faktorenanalyse gezeigt, dass der Untersucher häufig mit Schätzproblemen konfrontiert wird und unzulässige Lösungen das Ergebnis sind (Marsh, H. W./Bailey, M. 1991).
Der Test eines vollständigen Kausalmodells, d.h. eines Modells, das Faktorenmodelle und Kausalstrukturen zwischen mehreren Konstrukten erfasst, wird mit dem Test nomologischer Validität gleichgesetzt. Es erlaubt neben der Validierung der Messkonzepte den Test konkurrierender Hypothesen in einem Modell. Das Modell führt eine Validierung der Messkonzepte mit gleichzeitigem Test eines kausalen Netzwerks durch und sichert damit auch Validitätskriterien wie Konkurrent- und Prognosevalidität. Hierarchische Modelltests erlauben die Prüfung alternativer oder konkurrierender Theorien.
Eine typische Anwendung ist der Test des Einstellung-Verhalten-Modells (Ajzen, I./Fishbein, M. 1980). Es postuliert, dass die Einstellung und subjektive Norm die Verhaltens-Intention beeinflussen, die wiederum das Verhalten determiniert. Eine alternative Auffassung ist dagegen, dass die Einstellung das Verhalten direkt beeinflusst. Diese konkurrierenden Hypothesen sind in Abb. 3 dargestellt. Die Einstellung ist mit drei Indikatoren gemessen worden, die anderen Konstrukte mit jeweils zwei Indikatoren.
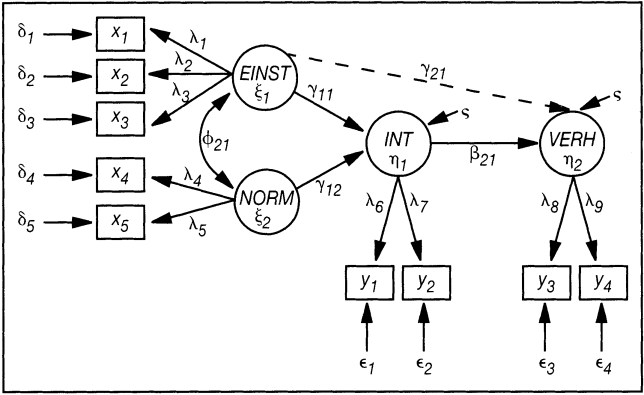
Abb. 3: Ein Kausalmodell zum Test von nomologischer Validität
Die Schätzung ergibt Faktorladungen λi zwischen 0,56 und 0,86, allerdings werden die Hypothesen des ersten Modells (ohne γ21) durch die Daten (bei Berücksichtigung der Stichprobengröße von n = 97), nach Prüfung der Fit-Indices nur im Grenzbereich gestützt. Die Schätzung des alternativen Modells führt dagegen zu einer signifikanten und besseren Anpassung, sodass in diesem Modellkontext die Einstellung das Verhalten direkt beeinflusst und die normativen Effekte nicht vorhanden sind. Die standardisierten Parameter des Strukturmodells und die Fit-Indices finden sich in Tab. 2.
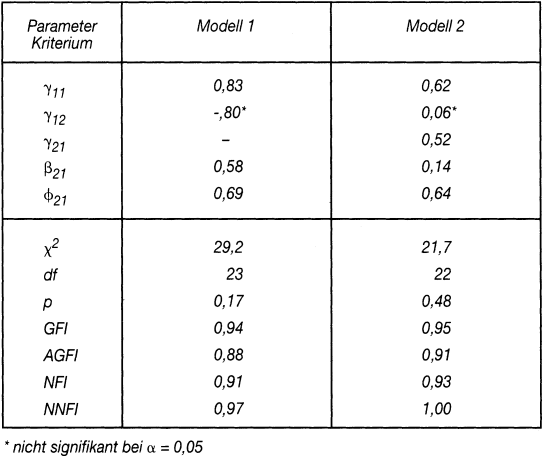
Tab. 2: Die standardisierten Parameter des Strukturmodells
Der hier dargestellte Modelltest kann nur einen Anhaltspunkt für die Möglichkeiten der Kausalanalyse geben. Das Potenzial liegt in der Prüfung komplexer Hypothesenstrukturen mit Validierung und in der Einsatzmöglichkeit zum Test von Faktorenstrukturen höherer Ordnung, der Anwendung des Modells auf Zeitreihen und Paneldaten sowie des Tests von Modellstrukturen mit Kontrolle unbeobachtbarer Einflussgrößen.
IV. Probleme der Kausalanalyse
Ein Großteil der Probleme der Kausalanalyse ergibt sich aus der Komplexität der Modellstrukturen, verbunden mit relativ strengen Annahmen für die Schätzung der Parameter. Der Anwender ist damit konfrontiert, dass die vorliegende Software auch Lösungen erzeugt, die den zulässigen Parameterbereich verlassen (z.B. negative Varianzen, standardisierte Regressionskoeffizienten größer eins etc.). Die Einführung von Restriktionen oder Spezifikations-»Tricks« durch sog. Phantom-Variablen können hier akzeptable Lösungen schaffen. Es sind aber jeweils eine Vielzahl von Kriterien zu prüfen, ehe der Forscher ein Modell dann als bewährt ansehen sollte.
Ein schwer zu lösendes Problem, besonders in komplexen Modellen, ist der Nachweis der Identifikation aller Modellparameter. Identifikationsprobleme können u.a. auftreten, wenn weniger als drei Indikatoren für die Faktoren vorliegen, Messfehlerkorrelationen vorhanden sind oder nicht rekursive Beziehungen geschätzt werden. Ein Modell wird als identifiziert bezeichnet, wenn alle frei zu schätzenden Parameter identifiziert sind. Dies ist nicht der Fall, wenn zwei unterschiedliche Parametersets die gleiche Kovarianzmatrix erzeugen. Eine notwendige Bedingung für Identifikation ist zunächst, dass die Zahl der frei zu schätzenden Parameter nicht die Zahl der unterschiedlichen Elemente in der Varianz-Kovarianz-Matrix übersteigt.
Diese Bedingung ist aber nicht hinreichend, sie gibt an, wann mit Sicherheit ein Modell nicht identifiziert ist. Streng genommen ist der Nachweis der Identifikation nur durch algebraische Auflösung der Gleichungsstruktur und den Nachweis, dass jeder Parameter eindeutig als Funktion der Varianzen und Kovarianzen ausgedrückt werden kann, möglich. Dies ist aber gerade bei komplexen Modellen kaum durchführbar. Im Allgemeinen muss sich der Forscher auf Ersatzkriterien verlassen, die in der Summe zwar eine relativ große, aber keine vollständige Sicherheit liefern.
Ein inhaltliches Problem ist die Logik des Chi2-Tests. Danach ist ein akzeptables Modell eines, welches durch die Daten nicht widerlegt werden kann. Wenn ein Modell nicht widerlegt werden kann, bleiben trotzdem andere – ähnlich gut »fittende« bzw. äquivalente (Lee, S./Hershberger, S. A. 1990) – Modelle auch nicht widerlegt.
Weiter besteht im Allgemeinen Unklarheit darüber, was unter der Kausalitätsinterpretation eines durch die Daten nicht zurückgewiesenen Modells zu verstehen ist. Kausalität einer Variablenbeziehung kann durch die Verfahren der Kausalanalyse nämlich nicht nachgewiesen werden. Multivariate statistische Verfahren repräsentieren nur eine Syntax, die hinsichtlich ihrer kausalen Interpretation neutral ist. Die Methode prüft deshalb nur Aussagen darüber, ob eine kausale Beziehung aufgrund der expliziten substanziellen Annahme des Forschers im Kontext einer modellierten Struktur statistisch existiert oder nicht. Im Rahmen des Marketing ist deshalb die Kausalinterpretation an eine Vielzahl von Kriterien zu knüpfen, wenn das Ergebnis einer Kausalanalyse für sozialtechnische Aussagen verwendet werden soll. Kausale Schlussfolgerungen beruhen letztendlich auf Kriterien, die außerhalb des Datenanalyse-Systems liegen.
Literatur:
Ajzen, I./Fishbein, M. : Understanding Attitudes and Predicting Social Behavior, Englewood Cliffs/NJ 1980
Annacker, D. : Unbeobachtbare Einflussgrößen in der strategischen Erfolgsfaktorenforschung, Wiesbaden 2001
Arbuckle, J. L. : Amos 6.0 User\'s Guide, Spring House/PA 2005
Bagozzi, R. P. : Casual Models in Marketing, New York 1980
Bagozzi, R. P. : A Prospectus for Theory Construction in Marketing: Revisited an Revised, in: Die Kausalanalyse. Instrument der empirischen betriebswirtschaftlichen Forschung, hrsg. v. Hildebrandt, L./Homburg, C., Stuttgart 1998, S. 44 – 81
Bentler, P. M./Wu, E.J. C. : EQS 6 for Windows User\'s Guide, Encino/CA 2002
Bollen, K. A. : Structural Equations with Latent Variables, New York 1989
Browne, M. W./Mels, G./Cowan, M. : Path Analysis: RAMONA: SYSTAT for DOS Advanced Applications, Evanston/IL 1994
Campbell, D. T./Fiske, J. D. : Convergent and Discriminant Validity by the Multitrait-Multimethod Matrix, in: Psychological Bulletin, 1959, S. 81 – 105
Carnap, R. : An Introduction to the Philosophy of Science, New York 1966
Chin, W. W. : PLS-Graph User\'s Guide Version 3.0, Houston 2001
Fritz, W. : Marktorientierte Unternehmensführung und Unternehmenserfolg, Stuttgart 1992
Hansmann, K.-W./Ringle, C. M. : SmartPLS Benutzerhandbuch, Hamburg 2004
Hartmann, W. M. : The CALIS Procedure: Extended User\'s Guide, Cary/NC 1992
Hildebrandt, L. : Wettbewerbssituation und Unternehmenserfolg, in: ZfB, 1992, S. 1069 – 1084
Hildebrandt, L. : Kausalanalytische Validierung in der Marktforschung, in: Die Kausalanalyse. Instrument der empirischen betriebswirtschaftlichen Forschung, hrsg. v. Hildebrandt, L./Homburg, C., Stuttgart 1998, S. 85 – 110
Hildebrandt, L. : Strukturgleichungsmodelle für die Konsumentenverhaltensforschung. Methodische Trends und Softwareentwicklungen, in: Konsumentenverhaltensforschung im 21. Jahrhundert, hrsg. v. Gröppel-Klein, A., Wiesbaden 2004, S. 541 – 564
Homburg, C. : Exploratorische Ansätze der Kausalanalyse, Frankfurt a.M. 1989
Hu, L.-T./Bentler, P. M. : Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria Versus New Alternatives, in: Structural Equation Modeling, H. 6/1999, S. 1 – 55
Jörskog, K. G./Sörbom, D. : LISREL 8: User\'s Reference Guide, Chicago 1996a
Jörskog, K. G./Sörbom, D. : PRELIS 2: User\'s Reference Guide, Chicago 1996b
Lee, S./Hershberger, S. A. : A Simple Rule for Generating Equivalent Models in Structural Equation Modelling, in: Multivariate Behavorial Research, 1990, S. 313 – 334
Lohmöller, J.-B. : LVPLS 1.6 Program Manual: Latent Variables Path Analysis with Partial Least-Squares Estimation, Zentralarchiv für empirische Sozialforschung, Universität zu Köln, Köln 1984
Marsh, H. W./Bailey, M. : Confirmatory Factor Analysis of Multitrait-Multimethod Data: A Comparison of the Behavior of Alternative Models, in: Applied Psychological Measurement, 1991, S. 47 – 70
McDonald, R. P. : A Simple Comprehensive Model for the Analysis of Covariance Structures, in: British Journal of Mathematical and Statistical Psychology, 1978, S. 59 – 72
McDonald, R. P. : A Simple Comprehensive Model for the Analysis of Covariance Structures: Some Remarks on Application, in: British Journal of Mathematical and Statistical Psychology, 1980, S. 161 – 183
Muthén, B. O./Muthén, L. K. : Mplus User\'s Guide, 4. A., Los Angeles 1998 – 2006
Neal, M. C./Boker, S. M./Xie, G. : MX: Statistical Modeling, 6. A., Richmond 2003
Satorra, A./Saris, W. E. : Power of the Likelihood Ratio Test in Covariance Structure Analysis, in: Psychometrika, 1985, S. 83 – 90
Steiger, J. : Structural Equation Modeling (SEPATH): Statistica/W, Tulsa/OK 1995
Temme, D./Kreis, H. : Der PLS-Ansatz zur Schätzung von Strukturgleichungsmodellen mit latenten Variablen: Ein Softwareüberblick, in: Handbuch PLS-Pfadmodellierung, hrsg. v. Bliemel, F./Eggert, A./Fassott, G. et al., Stuttgart 2005, S. 193 – 208
Trommsdorff, V. : Konsumentenverhalten, Stuttgart et al. 1989
|