Testverfahren

1. Definition. Die Formulierung von Hypothesen und deren Überprüfung mit Hilfe von empirischen Befunden ist eine typische Vorgehensweise der Wirtschaftswissenschaft und der Wirtschaftspraxis. Eine Hypothese wird aufgrund geeigneter Beobachtungen entweder aufrechterhalten oder als nicht haltbar verworfen. T. (im Sinne der Statistik; in der Psychologie wird das Wort in einer anderen Bedeutung verwendet) sind diejenigen Methoden der schließenden Statistik , mit welchen eine Entscheidung über die Beibehaltung oder Zurückweisung einer Hypothese mit Hilfe eines Stichprobenbefundes (Stichprobe) getroffen wird. Oft ist nötig, daß eine substanzwissenschaftliche Hypothese vor ihrer Prüfung in eine für T. geeignete statistische Formulierung übergeführt wird.
2. Beispiele für den Einsatz von T. a) Eine Lieferung von Metallteilen muß gemäß Vertragsbedingungen weniger als 8% Ausschuß enthalten. Die Einhaltung dieser Qualitätsnorm kann vom Abnehmer durch ein T. auf Stichprobenbasis überprüft werden. b) Die Qualität einer Lagerbuchführung bezüglich Korrektheit des Lagertotalwertes bzw. der einzelnen Postenwerte kann mit Hilfe eines T. kontrolliert werden; dazu muß für eine Stichprobe von Lagerposten der korrekte Wert durch körperliche Aufnahme festgestellt werden. c) Wird eine Regressionsanalyse durchgeführt, dann kann u.a. geprüft werden, ob ein bestimmter wahrer Regressionskoeffizient (Regressionsanalyse) der Grundgesamtheit von 0 verschieden ist bzw. einen bestimmten (Mindest-, Höchst-) Wert aufweist. d) Bei Vorliegen von Stichprobenbeobachtungen kann mit Hilfe von T. überprüft werden, ob eine bestimmte Variable eine Normalverteilung hat. e) Erfolgt eine Fertigung von Massenteilen auf mehreren parallelen Produktionsanlagen, so kann mit einem Testverfahren überprüft werden, ob die Gesamtproduktion homogen in dem Sinne ist, daß sich die Kennwerte bzw. Verteilungen der Teilproduktionen nicht unterscheiden.
3. Gegenstände von T. Ein T. kann zunächst einen bestimmten Wert oder auch Höchst- oder Mindestwert einer Kenngröße einer Variablen (Anteilswert; Durchschnitt ; Median; Varianz) zum Gegenstand haben (Parametertest, vgl.
2. a) bis c)). Soll das T. eine Entscheidung über eine Hypothese zum Verteilungsgesetz einer Variablen liefern, liegt ein Anpassungstest (vgl.
2. d)) vor. Die bisher genannten Teste betreffen den Ein-Stichproben-Fall, bei welchem die zu prüfende Hypothese nur eine einzige Grundgesamtheit betrifft. Daneben gibt es T. für den Vergleich von Kenngrößen bzw. Verteilungen zweier oder mehrerer Gesamtheiten (vgl.
2. e); Mehr-Stichproben-Fall).
4. Die Nullhypothese. Bei Parametertesten, weniger bei Anpassungstesten, wird der Gegenstand des T. häufig als Negation einer Arbeitshypothese konkretisiert. Er wird allgemein als Nullhypothese Ho  bezeichnet. Gelingt es, diese zur Ablehnung zu bringen, darf dies als Stützung der Arbeitshypothese gelten. Manchmal geht es bei einem T. nur um die Frage, ob Ho zutrifft oder nicht; dann spricht man von einem Signifikanztest . In anderen Fällen ist durch das T. eine Entscheidung zwischen Ho und einer speziellen Alternativhypothese H1 herbeizuführen.
5. Die Vorgehensweise im einzelnen. Einem T. liegt eine standardisierte Gedankenfolge zugrunde, welche hier beispielbezogen entwickelt wird. Zu prüfen sei (vgl.
2. a)) die Behauptung eines Lieferanten, der Ausschußanteil in seiner Lieferung betrage weniger als 8%. Der Abnehmer prüft daher q ³ 0,08  also die Nullhypothese, der Schlechtanteil betrage 8% oder mehr; ist diese zu verwerfen, kann er die Lieferung akzeptieren. Der Lieferung wird eine Stichprobe von n=100 Produkten entnommen. Man unterstellt bei der Durchführung des T., Ho sei richtig in der speziellen Form, daß q ³ 0,08 zutrfft. Unter dieser Annahme ermittelt man die Wahrscheinlichkeiten B (x½10; 0,08) dafür, daß höchstens x = 0, x = 1, ... schlechte Stücke vorkommen; sie ergeben sich aus der Binomialverteilung mit Parametern n = 100 und q ³ 0,08  gemäß nachfolgender Tabelle. Eine völlige Sicherheit dafür, daß Ho abgelehnt wird, wenn Ho falsch ist, bzw. nicht verworfen wird, wenn sie zutrifft, kann es nicht geben, wenn man keine Vollerhebung durchführt. Daher konzediert man eine bestimmte nahe 0 gelegene Wahrscheinlichkeit dafür, daß Ho fälschlicherweise abgelehnt wird; diese heißt Signifikanzniveau oder Irrtumswahrscheinlichkeit und wird  oft mit 0,05 oder 0,01 bemessen. Im gegebenen Beispiel ist anschaulich klar, daß Ho: q ³ 0,08 durch besonders niedrige Anzahlen schlechter Stücke in der Stichprobe in Frage gestellt wird. Daher wird bei einem Signifikanzniveau von a = 0,05 nach folgender Entscheidungsregel vorgegangen: H0 wird verworfen, falls x £ 3 in der Stichprobe resultiert; das Signifikanzniveau wird hierdurch auf etwa 3,7% statt 5% adjustiert, da 5% nicht exakt eingerichtet werden kann.                                                            


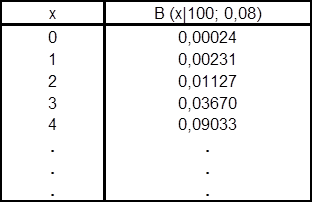
Die Entscheidung über H0 erfolgt anhand der aus der Stichprobe gewonnenen Ausprägung der Variablen "Anzahl der schlechten Stücke in der Stichprobe", die als Prüfvariable bezeichnet wird. Bei anderen T. werden andere Prüfvariablen verwendet, deren Verteilung unter H0 wiederum Grundlage für die Entscheidung über H0 ist. Die Menge der Ausprägungen der Prüfvariablen eines T., welche zur Ablehnung von H0 führt, heißt Ablehnungsbereich (kritische Region) des Tests. Bei Parametertesten sind grundsätzlich zweierlei Fragestellungen zu unterscheiden. Ist, wie im erörterten Beispiel, H0 eine Behauptung über einen Mindestwert eines Parameters, dann wird diese Hypothese abgelehnt, falls die Prüfvariable einen besonders niedrigen Wert aufweist. Der Ablehnungsbereich besteht also aus einem zusammenhängenden Intervall möglicher niedriger Werte der Prüfvariablen. Analoges gilt bei einer Behauptung über einen Höchstwert. In solchen Fällen spricht man von einer einseitigen Fragestellung. Hat H0 hingegen einen einzelnen Parameterwert zum Inhalt, wäre also etwa H0:  q ³ 0,08 zu prüfen, dann wäre diese Hypothese abzulehnen, wenn die Prüfvariable x besonders niedrige oder besonders hohe Werte annimmt. Der Ablehnungsbereich besteht in einem solchen Fall aus zwei getrennten Teilbereichen. Dann liegt eine zweiseitige Fragestellung vor.
6. Fehlerarten bei der Durchführung von T. Bei jedem T. sind richtige Entscheidungen und Fehlentscheidungen möglich. Richtig entschieden wird, falls H0 falsch ist und abgelehnt wird, und falls H0 richtig ist und nicht abgelehnt wird. Wird H0 fälschlich abgelehnt, liegt ein Fehler
1. Art vor; die (Höchst-) Wahrscheinlichkeit hierfür wird durch das Signifikanzniveau vorgegeben. Ein Fehler
2. Art ist gegeben, wenn H0 falsch ist und nicht als falsch erkannt wird. Die Wahrscheinlichkeit für einen Fehler
2. Art mag im Einzelfall sehr hoch sein. Ist im obigen Beispiel etwa q = 0,05 der wahre Schlechtanteil, H0 also falsch, und wird, wie festgelegt, H0 abgelehnt, falls x £ 3 resultiert, dann ist die Wahrscheinlichkeit eines Fehlers
2. Art          1 - B (3½100; 0,05) = 0,74216 Ein solcher Fehler ist hier vor allem für den Lieferanten nachteilig.
7. Übersicht über T. Eine erste und ältere Gruppe von T. ist durch die Voraussetzung gekennzeichnet, die interessierenden Variablen seien normalverteilt ("klassische" parametrische T.). Neuerdings werden oft T. bevorzugt, die diese Voraussetzung nicht benötigen (nichtparametrische, verteilungsfreie T.). Zu den parametrischen T. gehört der t-Test (Prüfung eines Erwartungswertes) im Ein-Stichproben-Fall, der t-Test (Vergleich zweier Erwartungswerte) im Zwei-Stichproben-Fall, der F-Test (Vergleich zweier Varianzen) im Zwei-Stichproben-Fall und im Mehr-Stichproben-Fall  (Varianzanalyse). Nichtparametrische Alternativen zum Ein-Stichproben-t-Test sind der Vorzeichentest und der Vorzeichen-Rang-Test von Wilcoxon, zum Zwei-Stichproben-t-Test der Wilcoxon-Mann-Whitney-Test, zum Zwei-Stichproben-F-Test der Test von Siegel-Tukey und zum Mehr-Stichproben-F-Test der Kruskal-Wallis-Test. Anpassungsteste (Prüfung einer Verteilungshypothese im Ein-Stichproben-Fall; Vergleich von Verteilungen im Zwei-Stichproben-Fall) sind der Chi-Quadrat-Test und der Kolmogorov-Smirnov-Test. Bei den klassischen normalverteilungsgebundenen T. lassen sich bestimmte Optimalitätseigenschaften nachweisen. Für die nichtparametrischen T. spricht der Vorteil der viel weniger restriktiven Anwendungsvoraussetzungen.

Literatur: J. Bleymüller/G. Gehlert/H. Gülicher, Statistik für Wirtschaftswissenschaftler.
8. A., München 1992, insbes. Kap. 16-19. J. Hartung, Statistik. 10. A., München 1995, insbes. Kapitel III und IV.  E. Schaich/A. Hamerle, Verteilungsfreie statistische Prüfverfahren. Berlin, Heidelberg, New York, Tokyo 1984. E. Schaich, Schätz- und Testmethoden für Sozialwissenschaftler.
2. A., München 1990.