Inhaltsübersicht I. Grundlagen II. Effektivzinsrechnung auf der Basis der internen Zinsfußmethode III. Effektivzinsen im Vergleich I. Grundlagen Die effektiven Kosten bzw. Erlöse von Finanzgeschäften werden durch eine Reihe von Konditionsbestandteilen beeinflusst. Neben dem sog. Nominalzins determinieren beispielsweise bei Kreditgeschäften das Disagio (Damnum), die Bearbeitungsgebühren sowie Zinszahlungs- und Tilgungsmodalitäten den Kreditpreis. Die Zinsgröße, zu der all diese zinsbestimmenden Faktoren verdichtet werden und mit der der effektive Kreditpreis und allgemein der Kostensatz für Geldanlagen bzw. die Rendite für Finanzierungen zum Ausdruck gebracht werden soll, wird als Effektivverzinsung bezeichnet. Angesichts der vielfältigen Gestaltungsmöglichkeiten von Finanzgeschäften besteht der vorrangige Zweck der Effektivzinsrechnung darin, verschiedene Finanzierungs- respektive Geldanlagemöglichkeiten miteinander vergleichbar zu machen (Schierenbeck, H./Rolfes, B. 1988). Dies erfordert ein einheitliches und die unterschiedlichen Modalitäten erfassendes Berechnungsverfahren, das sowohl für den institutionellen Geldhandel und Kapitalverkehr als auch entsprechend der Preisangabenverordnung (PangV) für Geldgeschäfte zwischen Kreditinstituten und ihren Kunden gilt. Gerade für letztgenannte Geschäfte ist eine vergleichbare Größe unter dem Aspekt des Konsumentenschutzes unerlässlich, da Kunden so vor versteckten Konditionen geschützt werden können. Aufbauend auf den zinsfußorientierten Methoden der allgemeinen Wirtschaftlichkeitsrechnung haben sich unterschiedliche Verfahren der Effektivzinsrechnung herausgebildet, die sich auf drei Grundtypen zurückführen lassen: - die (traditionelle) statische Methode, - die dynamische reale Zinsfußmethode und - die dynamische interne Zinsfußmethode. Den beiden erstgenannten Verfahren kommt aufgrund der ihnen anhaftenden methodischen Mängel bzw. erforderlichen subjektiven Annahmen in der Finanzpraxis nahezu keine Bedeutung zu und sie werden daher von der weiteren Erörterung ausgenommen (für eine ausführliche Analyse vgl. Schierenbeck, H./Rolfes, B. 1988). Allein die interne Zinsfußmethode erfüllt die Anforderungen an die Effektivzinsrechnung, nämlich erstens die ausschließliche Berücksichtigung der mit einem Geldgeschäft für beide Geschäftspartner (mit unterschiedlichen Vorzeichen) verbundenen Originär-Zahlungsreihe sowie zweitens die einheitliche und von individuellen Wiederanlage- oder Nachfinanzierungsmöglichkeiten losgelöste Bewertung von Zahlungsreihen. Allerdings bieten sich auch im Rahmen der internen Zinsfußmethode noch unterschiedliche Varianten der Effektivzinsrechnung an, und es bedarf einer entsprechenden Konvention darüber, welche der mit diesen Verfahrensvarianten gemachten Prämissen zugrunde gelegt werden sollen. II. Effektivzinsrechnung auf der Basis der internen Zinsfußmethode 1. Die Interpretation des internen Zinsfußes Der interne Zinsfuß (vgl. Rolfes, B. 1998) ermittelt sich aus der Zahlungsreihe des Grundgeschäfts als derjenige Zinsfuß (r), mit dem die Rückzahlungen (Et) auf den Zeitpunkt Null abgezinst werden müssen, damit die sich daraus ergebenden Rückzahlungsbarwerte in ihrer Summe genau dem Kreditauszahlungsbetrag (A0) entsprechen. 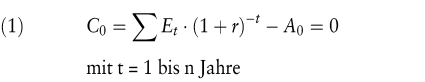Gesucht ist also mit anderen Worten der Zinssatz, bei dem der Kapitalwert (C0) gleich Null wird: Die Bestimmungsgleichung 1) macht deutlich, dass der interne Zinsfuß einer Zahlungsreihe im Mehrperiodenfall formal eine für jede Periode identische und damit zeitlich durchschnittliche Verzinsung (des eben unter Berücksichtigung dieser Verzinsung noch gebundenen Kapitals) darstellt. Dieser Zusammenhang und die Tatsache, dass der interne Zinsfuß im Normalfall noch einer weiteren Bedingung genügt, nämlich dass der effektive Kapitaleinsatz während der Laufzeit auf null zurückgeführt wird, soll anhand eines einfachen Kreditbeispiels verdeutlicht werden. Zugrunde gelegt wird ein vierjähriger Kredit über nominal 4000 GE bei einer Auszahlung von 90% (Disagio 10%), also in Höhe von 3600 GE. Die nominelle Tilgung soll in vier gleichen Jahresraten von je 1000 GE erfolgen, der Nominalzins beläuft sich auf 5% (bezogen auf das jeweils noch gebundene Nominalkapital). 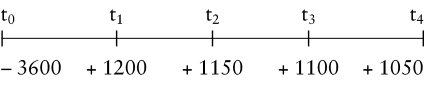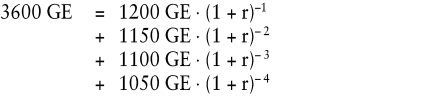Aus diesem Kreditvertrag ergibt sich folgende Zahlungsreihe des Kredites: Für diese Zahlungsreihe ergibt sich nun nachfolgende Ausgangsgleichung zur Bestimmung des internen Zinsfußes: Der interne Zinsfuß (r) und damit der Effektivzins des Kreditgeschäftes wird durch iteratives Interpolieren ermittelt und beträgt 9,8% (zu Interpolation und Näherungsverfahren vgl. Perridon, L./Steiner, M. 1999). Es handelt sich bei diesem Zinssatz um die „ Eigenverzinsung “ des jeweils noch eingesetzten Restkapitals (vgl. Abb. 1). 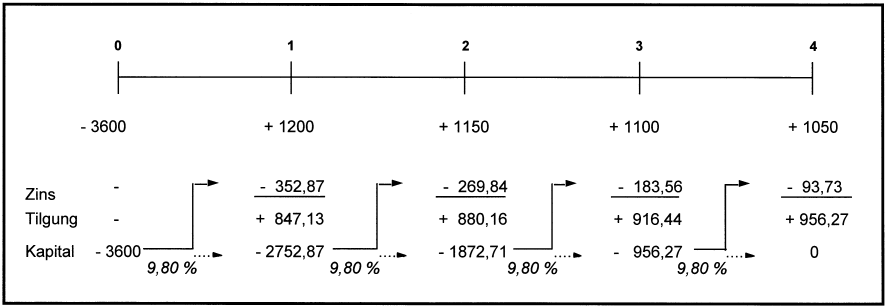Abb. 1: Der interne Zinsfuß gibt die Verzinsung des jeweils noch nicht amortisierten Restkapitals an Der Effektivzins spaltet den Kapitaldienst über die Laufzeit gerade so in Zins- und Tilgungsanteile auf, dass zum Laufzeitende im vierten Jahr der Kapitaldienst in Höhe von 1050 GE exakt ausreicht, um den effektiven Zinsertrag des vierten Jahres (93,73 GE) zzgl. des in diesem Jahr noch gebundenen Restkapitals (956,27 GE) abzudecken. Als periodisch konstanter Zinssatz erfüllt der interne Zinsfuß somit zwei formale Bedingungen. Zum einen kennzeichnet er den Zinssatz, bei dem der Kapitalwert gleich Null wird. Zum anderen stellt er sicher, dass durch die laufende Tilgungsverrechnung während der Laufzeit auch der effektive Kapitaleinsatz auf Null zurückgeführt wird. Allerdings gilt der interne Zinsfuß auch stets nur für die Zahlungsreihe als Ganzes. Dies bedeutet, dass sich bei einer Veränderung der Zahlung im Zeitpunkt vier nicht nur der Effektivzins in der vierten Periode, sondern auch in den ersten drei Perioden verändern würde. Insofern hängt die „ Vereinnahmung “ des effektiven Zinsertrages im ersten Jahr sowie die daraus abgeleitete effektive Tilgung auch von den Zahlungen in späteren Jahren ab. 2. Die Umsetzung der internen Zinsfußmethode in der Finanzpraxis Die in der Finanzpraxis gebräuchlichen Verfahren der Effektivzinsberechnung stellen Varianten der internen Zinsfußrechnung dar. Sie führen jedoch nur dann zu unterschiedlichen Effektivzinssätzen, wenn Zahlungsreihen durch sog. „ gebrochene “ Laufzeiten und/oder unterjährige Zahlungen gekennzeichnet sind. Im obigen Beispiel des vierjährigen Kredites mit ausschließlich jährlichen Zahlungen würden somit alle Varianten zum gleichen Effektivzins von 9,80% führen. Die wichtigste und im Folgenden näher zu behandelnde Variante stellt die Effektivzinsrechnung nach ISMA (International Securities Market Association; früher AIBD, Association of International Bond Dealers) dar (Schierenbeck, H./Rolfes, B. 1988; Dartsch, 1998). Das Verfahren nach PAngV (Preisangabenverordnung), das bisher wegen nationaler Vorschriften hohe Relevanz besaß, soll an dieser Stelle daher nur kurz behandelt und mit der ISMA-Methode verglichen werden. Der wesentliche Unterschied zwischen der Effektivzinsrechnung nach PAngV und dem Effektivzins nach ISMA besteht darin, dass bei erstgenanntem Verfahren unterjährig mit linearer Verzinsung, also ohne Zinseszinsen, gerechnet wird, während bei der ISMA-Methode unterjährig mit exponentieller Verzinsung – also mit Zinseszinsrechnung auch im unterjährigen Bereich – gearbeitet wird. Die Tatsache, dass nach der PAngV erst nach jeweils einem vollen Nutzungszeitraum von einem Jahr Zinsen verrechnet, d.h. dem Kapital zugeschlagen werden, hat zwei wichtige Konsequenzen: Zum Ersten verringern alle unterjährigen Zahlungen, die zwischen den Kapitalisierungszeitpunkten liegen, das kalkulatorische Zinskapital in voller Höhe. Zum Zweiten wird bei gebrochenen Laufzeiten (wie z.B. bei 1 ¼ oder 1 ½ Jahren) wegen der Vorschrift der PAngV, dass erst nach einem vollen Jahr ab Kreditgewährung eine kalkulatorische Zinskapitalisierung vorzunehmen ist, der sog. „ gebrochene “ Teil der Laufzeit an das Ende der Gesamtlaufzeit gelegt. Nach der ISMA-Methode hingegen werden „ gebrochene “ Laufzeiten nicht besonders behandelt, da hier eine kontinuierliche, d.h. bei tageweiser Abrechnung, tägliche Zinskapitalisierung unterstellt wird. 3. Der Effektivzins nach ISMA Die Effektivzinsberechnung nach ISMA soll im Folgenden anhand eines Beispiels dargestellt und erläutert werden. Es sei von einem Kredit über nominal wiederum 4000 GE ausgegangen, der zu 95% (3800 GE) ausgezahlt wird. Getilgt werden soll in vier gleich hohen Halbjahresraten in Höhe von jeweils 1000 GE. Auch die Nominalzinsen (5% auf das jeweils noch nicht getilgte Nominalkapital) werden halbjährlich zusammen mit den Tilgungszahlungen geleistet. Die Zahlungsreihe dieses Kredites hat dann folgendes Aussehen: Mon. 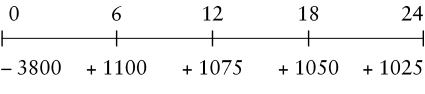Bei der Effektivzinsberechnung nach ISMA wird nun eine stetige Verzinsung zugrunde gelegt, also – zeitdiskret ausgedrückt – sekündlich, stündlich oder (wie im Weiteren dargestellt) täglich mit Zinseszinsen kalkuliert. Die für einen Tag anfallenden Zinsen werden – unabhängig davon, ob eine Zahlung erfolgt oder nicht – täglich kapitalisiert und am nächsten Tag wieder mitverzinst. 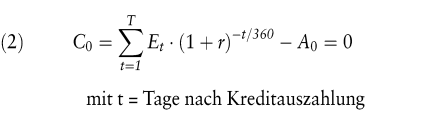Formal kommt dies in der Kapitalwertgleichung nach ISMA durch die jeweils direkte exponentielle Abzinsung einer jeden Rückzahlung auf den Auszahlungszeitpunkt zum Ausdruck: Faktisch bedeutet die exponentielle Abzinsung, dass jede Rückzahlung stufenweise vom Zahlungstag Tag für Tag bis zum Auszahlungszeitpunkt abgezinst wird. Mit der Annahme der exponentiellen Verzinsung wird die Zinsschuld täglich dem Kapital zugeschlagen. Die tatsächlichen Zahlungstermine bleiben somit ohne Einfluss auf die kalkulatorische Zinsverrechnung. 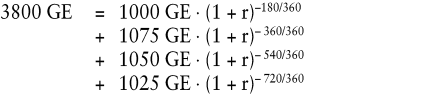Für die Kreditzahlungsreihe ergibt sich nach der ISMA-Methode folgende Gleichung zur Bestimmung des Effektivzinssatzes: Aus dieser Bedingungsgleichung ergibt sich ein Effektivzins nach ISMA in Höhe von 9,60%. Abb. 2 zeigt die zugehörige Zins- und Tilgungsverrechnung. 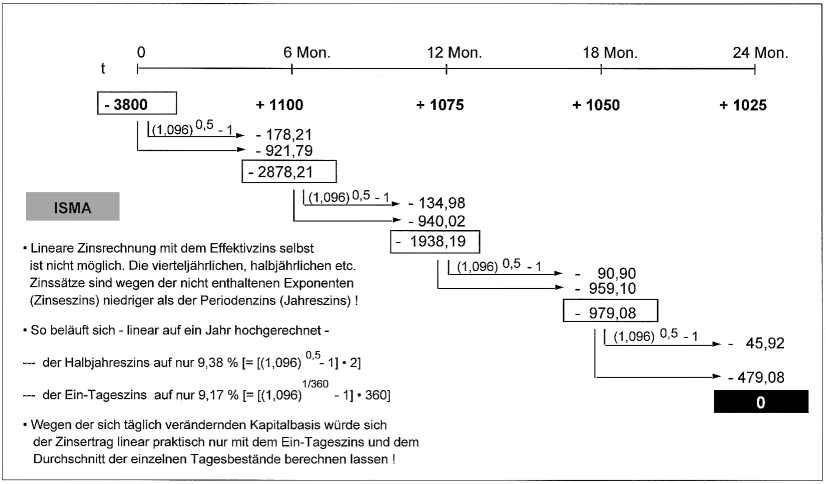Abb. 2: Effektive Zins- und Tilgungsrechnung nach ISMA Die Zahlungszeitpunkte dürfen hier nicht als Zinsverrechnungszeitpunkte interpretiert werden, denn bei der Effektivverzinsung nach ISMA findet zu diesen Zeitpunkten lediglich eine Zahlungsverrechnung mit dem bis dahin aufgelaufenen Zinskapital statt. Die Zinsverrechnung erfolgt dagegen täglich. Aus diesem Grund entspricht das der Zinsberechnung zugrunde gelegte Zinskapital schon nach einem Tag nicht mehr dem ausgezahlten Kapital in Höhe von 3800 GE. Vielmehr hat sich die Kapitalschuld nach einem Tag schon auf 3800,97 GE erhöht. Um dies berechnen zu können, muss allerdings der (linear auf ein Jahr hochgerechnete) Ein-Tages-Zins in Höhe von 9,17% verwendet werden, weil sich die exponentielle Effektivzinsgröße nicht auf (lineare) Kapitalbewegungen beziehen lässt. Mit der exponentiellen Zinsrechnung wird die Restkapitalbewegung vielmehr im Zins selbst erfasst. III. Effektivzinsen im Vergleich Zur Beurteilung verschiedener Effektivzinsverfahren ist das Augenmerk insbesondere darauf zu legen, welche Prämissen bei den einzelnen Verfahren für die Schaffung einer Vergleichbarkeit zwischen unterschiedlichen Finanzgeschäften gemacht werden müssen. Diese Prämissen gewinnen um so mehr an Bedeutung, je stärker sich die Laufzeiten bzw. Kapitalbindungen der verglichenen Finanzalternativen voneinander unterscheiden. Der besondere Vorteil der ISMA-Methode gegenüber der alten PAngV-Methode besteht nun darin, dass die ISMA-Methode implizit eine Zinseszinsprämisse enthält, sodass eine Fristigkeitsdifferenz beim Vergleich zweier Finanzalternativen über eine rechentechnisch implizierte Differenzinvestition bei der kürzeren Finanzalternative quasi „ automatisch “ ausgeglichen wird. Bei der PAngV-Methode hingegen müsste diese Zinseszinsprämisse explizit hinzugefügt werden, da sich sonst bei einem Vergleich von in der Laufzeit bzw. Kapitalbindung unterschiedlichen Finanzalternativen auch verschiedene Effektivzinssätze ergeben würden. Dieser Zusammenhang sei an einem Beispiel verdeutlicht, bei dem drei Anlagealternativen mit gleichem Nominalzins (12% p.a.) verglichen werden (vgl. Abb. 3). 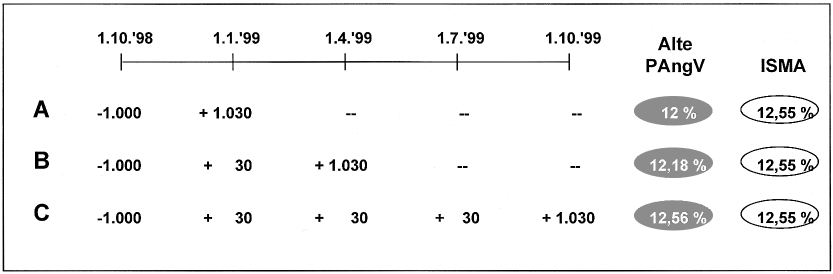Abb. 3: Effektivzinsen im Vergleich Bei der Alternative A handelt es sich um eine 3-Monats-Geldanlage mit zusammenfallender Zins- und Tilgungszahlung nach Ablauf von 90 Tagen. Alternative B stellt eine halbjährige Geldanlage mit zwischenzeitlicher Zinszahlung nach einem Vierteljahr dar, während Alternative C bei ebenfalls quartalsweiser Zinszahlung über ein Jahr läuft. Weil beim PAngV-Effektivzins stets nur der Anlagezeitraum isoliert betrachtet wird, weisen bei dieser Methode alle drei Alternativen unterschiedliche Effektivzinssätze auf. So können bei Alternative A (12%), bei der die erste Zahlung auch gleichzeitig die Schlusszahlung darstellt, keine zwischenzeitlichen „ Einspareffekte “ auftreten. Anders verhält es sich bei Alternative B, deren PAngV-Effektivzins sich auf 12,18% beläuft. Die zwischenzeitliche (Zins-) Zahlung, die bis zum Ende der Laufzeit aufgezinst wird, verringert hier das effektive Zinskapital, sodass der Effektivzins steigt. Bei Alternative C wird dieser Wiederverzinsungs- rsp. Kapitaleinspareffekt durch drei zwischenzeitliche Quartals-Zinszahlungen noch verstärkt, hier beläuft sich der Effektivzins nunmehr auf 12,56%. Hingegen wird beim Effektivzins nach ISMA der unterjährige Zahlungseffekt bereits bei den Alternativen A und B erkannt und als kontinuierlich angenommen, sodass sich auch bei diesen genauso wie bei Alternative C der gleiche Effektivzins i.H.v. 12,55% einstellt. Bei einer Vorteilhaftigkeitsbestimmung würden nach ISMA somit alle Alternativen als gleichwertig angesehen, weil z.B. für Alternative A unterstellt wird, dass für die kommenden Quartale gleichartige Anschlussgeschäfte zu der gleichen Kondition möglich sind, was insgesamt zur gleichen Zahlungsreihe wie bei Alternative C führen würde. Über explizite, gleichkonditionierte Zusatzgeschäfte ließe sich, wie das Beispiel zeigt, auch nach der alten PAngV-Methode die Vergleichbarkeit zweier Geschäfte mit unterschiedlicher Fristigkeit konstruieren und der Effektivzins für die Gesamtzahlungsreihe (12,56%) berechnen. Die nach der PAngV explizit zu treffenden Verzinsungs-Annahmen offenbaren dem Vergleichenden zugleich die unterschiedliche Qualität etwa der Alternativen A und C. Der ISMA-Zins dagegen, der aufgrund seiner impliziten täglichen Zinskapitalisierungsprämisse gleiche Renditen aufweist, zeigt für Alternative A immer dann einen zu positiven „ p.a. “ -Effektivzins an, wenn das Zinsniveau sinkt und vice versa. Doch trotz oder gerade wegen obiger Argumentation spricht auch bezüglich des Vergleichsproblems unterschiedlicher Fristigkeiten vieles für den ISMA-Zins. Die nach der alten PAngV-Methode umständliche Explizierung der Anschlussprämisse ist gleich implizit enthalten, was eine Vergleichbarkeit deutlich erleichtert. Auch die unterstellte Differenzinvestition zum Effektivzins selbst scheint sinnvoll, denn dies ist die im Entscheidungszeitpunkt für ein Geschäft gültige Verzinsung, zu der sich, wenn keine Marktzinsänderung stattgefunden hat, entsprechende Anschlussgeschäfte tätigen lassen. So können außerdem die Rendite und das (Zinsänderungs-) Risiko isoliert voneinander betrachtet werden. Das Wissen darüber, dass der ISMA-Zins bei Alternative A lediglich 3 Monate gesichert ist, während er bei Alternative C für ein Jahr feststeht, sollte einem Anleger unterstellt werden dürfen. Dieser müsste dann bei zwei Alternativen mit gleichem Effektivzins aufgrund seiner Zinserwartung selbst entscheiden, welche Anlagefrist ihm am vorteilhaftesten erscheint. Literatur: Perridon, L./Steiner, M. : Finanzwirtschaft der Unternehmung,10. A., München 1999 Rolfes, B. : Moderne Investitionsrechnung, 2. A., München et al. 1998 Rolfes, B./Dartsch, A. : Effektivzinsverfahren in der Bankkalkulation, in: WISU 1998, S. 380 – 386 Schierenbeck, H. : Grundzüge der Betriebswirtschaftslehre, 14. A., München et al. 1999 Schierenbeck, H./Rolfes, B. : Endscheidungsorientierte Margenkalkulation, Frankfurt 1988 Wimmer, K./Stöckl-Pukall, E. : Die Preisangabenverordnung der Banken, München 1998