Inhaltsübersicht I. Grundlagen II. Starre und flexible Planung III. Flexible Planungsmethoden IV. Realoptionen I. Grundlagen Im betrieblichen Planungsprozess werden die Ziele der Unternehmung festgelegt, alternativ mögliche Maßnahmen zur Zielerreichung ermittelt sowie aufgrund von Prognosen die für die alternativen Aktionen zu erwartenden Konsequenzen bestimmt. Um eine zieloptimale Vorgehensweise zu finden, müssen Bewertungsmethoden herangezogen werden, die insbesondere zwei Merkmale ins Kalkül einbeziehen. Erstens, Realprobleme weisen i.d.R. eine zeitliche Struktur auf, sodass ein mehrstufiges oder dynamisches Entscheidungsproblem vorliegt (Dinkelbach, W.  1989). Die Handlungsalternativen beinhalten hier eine Folge von Aktionen. Entscheidungen über die Gegenwart und die Zukunft müssen getroffen werden, wobei aufgrund der zumeist bestehenden Interdependenzen die Festlegung dieser gegenwärtigen und zukünftigen Maßnahmen gleichzeitig erfolgen muss (Hax, H.  1993; Franke, G./Hax, H.  1999). Zweitens, ist die Handlungskonsequenz unsicher, da meist nicht mit Sicherheit bekannt ist, welcher Umweltzustand in der Zukunft tatsächlich eintritt (Ossadnik, W.  1994). Somit liegt ein Entscheidungsproblem unter unvollkommener Information vor. Flexible Planungsmethoden dienen dazu, die optimale Vorgehensweise festzulegen, wobei sowohl der Faktor Zeit als auch der sich im Zeitablauf verbessernde Informationsstand der Planungsträger Berücksichtigung finden. II. Starre und flexible Planung Grundsätzlich lassen sich zwei unterschiedliche Planungsansätze unterscheiden. Werden alle zukünftigen Maßnahmen der Teilperioden des Planungszeitraums auf Grundlage der zum Planungszeitpunkt vorhandenen Information über zukünftige Umweltentwicklungen definitiv festgelegt, dann spricht man von starrer Planung. Hier wird zwar die Abhängigkeit der Aktionen von zeitlich vorgelagerten Aktionen berücksichtigt, die Maßnahmen für zukünftige Zeitpunkte aber ohne Rücksicht darauf festgelegt, welcher Umweltzustand im jeweiligen Zeitpunkt gegeben sein wird. Eine evtl. Planrevision wird hier nur im Nachhinein in Betracht gezogen. Die starre Planung kann jedoch, auch bei laufender Planrevision, zu Fehlentscheidungen führen, weil der Einfluss von zukünftigen Anpassungsmöglichkeiten nicht in Betracht gezogen wird (Inderfurth, K.  1982). Die flexible Planung hingegen versucht, die verschiedenen möglichen Umweltentwicklungen von vornherein in die Planung einzubeziehen. Gegenwärtige und zukünftige Aktionen werden simultan geplant, im Unterschied zur starren Planung werden die zukünftigen Maßnahmen jedoch vom Eintreten der ex ante für möglich gehaltenen Umweltzustände abhängig gemacht. Somit werden bei flexibler Planung Verbesserungen des Informationsstandes der Entscheidungsträger im Zeitablauf explizit berücksichtigt. Die Maßnahmen werden also nicht definitiv festgelegt, sondern es wird ein System bedingter Teil- oder Eventualpläne für unterschiedliche Umweltzustände ermittelt. III. Flexible Planungsmethoden Optimale Entscheidungsregeln oder Strategien bei flexibler Planung können mithilfe unterschiedlicher Lösungsverfahren ermittelt werden. Für Voraussetzungen und Durchführung sei auch verwiesen auf Inderfurth und Schneeweiß (Inderfurth, K.  1982; Schneeweiß, C.  1992). 1. Ermittlung flexibler Pläne mit dem Zustandsbaum-Verfahren Die optimale Vorgehensweise kann auf Grundlage eines Zustandsbaums ermittelt werden (Inderfurth, K.  1982; Franke, G./Hax, H.  1999). Ein Zustandsbaum erfasst die möglichen Entwicklungen der Umwelt über den Planungszeitraum, sowie die (subjektiven) Einschätzungen des Planungsträgers. In Abb. 1 ist ein Zustandsbaum gegeben, der die möglichen Entwicklungen der Nachfrage über einen Planungshorizont von 2 Jahren abbildet. Der Investor erwartet also z.B. eine hohe Nachfrage (H) in Periode 1 mit Wahrscheinlichkeit 0.4. War die Nachfrage in Periode 1 hoch, so erwartet er eine Fortsetzung der hohen Nachfrage in Periode 2 mit Wahrscheinlichkeit 0.8 und eine niedrige Nachfrage (N) nur mit Wahrscheinlichkeit 0.2 (bedingte Wahrscheinlichkeiten). Für jeden Zustand des Zustandsbaumes wird nun ein Maßnahmenkatalog aufgestellt. Nehmen wir z.B. an, dass in den Zuständen 1, 2 und 3 jeweils 2 Projekte durchgeführt werden können, nämlich A und B in 1, C und D in 2, E und F in 3, dann können wir binäre Variablen xj für j aus J = {A,B,C,D,E,F} einführen, wobei xj = 1 bedeutet, dass das Projekt j im jeweiligen Zustand durchgeführt wird. Jedes Projekt ist dabei genau einem Zustand zugeordnet und identische Projekte, die in verschiedenen Zuständen durchgeführt werden können, werden als unterschiedlich behandelt. Projekt j wirft im Zustand s den Einzahlungsüberschuss esj ab, wobei s jenen Zustand, in dem das Projekt durchgeführt werden kann, sowie die in späteren Perioden folgenden Zustände, durchläuft. Für alle übrigen Zustände gilt esj=0. Für das Projekt C würden sich also die folgenden Einzahlungsüberschüsse für die 7 möglichen Zustände ergeben: (0, e2C, 0, e4C, e5C, 0, 0). Im Falle eines risikoneutralen Investors, der sich nur am Erwartungswert der Zahlungen orientiert, kann der flexible Plan nun sehr einfach als Lösung einer linearen Optimierungsaufgabe mit Binärvariablen ermittelt werden. Aus obigen Angaben kann zunächst der erwartete Kapitalwert eines Projekts auf Basis der im Zustandsbaum gegebenen Wahrscheinlichkeiten berechnet werden. Als Zielgröße des Gesamtprogramms lässt sich dann die mit den Binärvariablen gewichtete Summe der einzelnen Kapitalwerte der Projekte heranziehen. Zusätzlich können noch Nebenbedingungen, die z.B. aus der begrenzten Verfügbarkeit der Finanzierungsmittel resultieren, berücksichtigt werden (Hax, H.  1993; Franke, G./Hax, H.  1999). 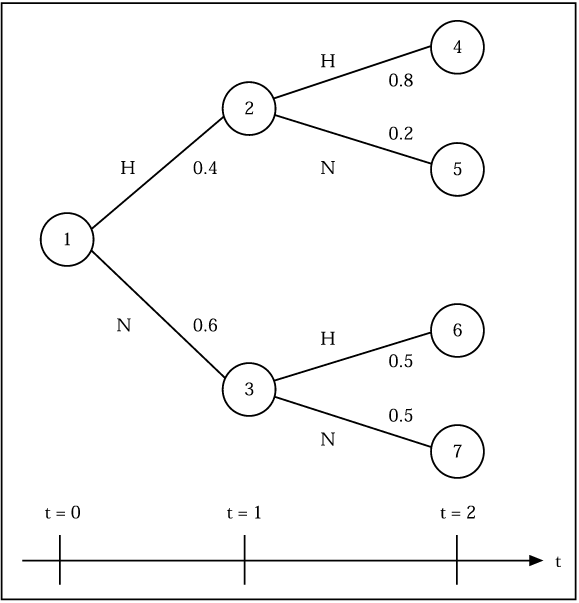Abb. 1: Zustandsbaum für ein dynamisches Entscheidungsproblem 2. Ermittlung flexibler Pläne mit dem Entscheidungsbaum-Verfahren Im Rahmen dieses Lösungsverfahrens wird der Zustandsbaum zu einem Entscheidungsbaum erweitert. Bei der Diskussion dieser Methode werden wir uns auf das folgende einfache Beispiel zur Investitionsplanung beziehen (vgl. Kruschwitz, L.  1998). Ein Investor hat einen Planungszeitraum von 2 Jahren. Er kann im Zeitpunkt t=0 entweder eine kleine Anlage bauen (A) oder eine große Anlage mit doppelter Kapazität (2A) errichten. Im Zeitpunkt t=1 hat er 3 Möglichkeiten: entweder die Anlage mit einfacher Kapazität auf doppelte Kapazität erhöhen (A auf 2A), eine große Anlage auf einfache Kapazität verkleinern (2A auf A) oder aber nichts zu tun (NT). Die zukünftige Entwicklung der Nachfrage ist unsicher und damit hängen die Rückflüsse aus dem Verkauf der Produkte nicht nur von den Entscheidungen des Investors über die Anlagenpolitik, sondern auch von der Nachfrageentwicklung ab. Die Einschätzung des Investors über die Entwicklung der Nachfrage sei wie in Abb. 1. Das Entscheidungsproblem des Investors kann mit Hilfe eines Entscheidungsbaums, der die möglichen Alternativen für den Investor, die unsichere Entwicklung der Nachfrage und die resultierenden Rückflüsse erfasst, dargestellt werden (Abb. 2). An den viereckig gezeichneten Entscheidungsknoten ist der Investor jeweils aufgefordert, eine jener Alternativen auszuwählen, die an den von dort ausgehenden Entscheidungskanten angegeben sind (im Beispiel A, 2A oder NT). An den rund gezeichneten Zufallsknoten werden an den von dort ausgehenden Zufallskanten die möglichen Umweltentwicklungen (hohe oder niedrige Nachfrage) mit deren Wahrscheinlichkeiten (in Klammern) angegeben. Bei Kenntnis des Kalkulationszinsfusses und der jeweiligen Rückflüsse in Abhängigkeit von der Nachfrageentwicklung und der Entscheidung für die verschiedenen Zeitpunkte lässt sich dann der Barwert der unterschiedlichen Vorgehensweisen ermitteln. Im vorliegenden Beispiel seien der Einfachheit halber an den Endknoten nur die jeweiligen Kapitalwerte (ohne Darstellung der Berechnung) angegeben. Es sei nun zunächst demonstriert, wie sich die Anlagenpolitik bei starrer und flexibler Planung unterscheidet. Bei starrer Vorgehensweise wird auf Grundlage der Wahrscheinlichkeiten für die Umweltentwicklung zum Zeitpunkt 0 eine optimale Politik (unabhängig von der tatsächlichen zukünftigen Nachfrage) fix festgelegt, und zwar z.B. auf Basis der erwarteten Kapitalwerte. Es stehen vier Alternativen zur Auswahl mit den folgenden erwarteten Kapitalwerten: A und NT (KW=190); 2A und NT (KW=197); A auf 2A (KW=193); 2A auf A (KW=168). Diese Alternativen entsprechen also der Anschaffung einer kleinen bzw. großen Anlage und Beibehalten derselben in Periode 2, bzw. Anschaffung einer kleinen bzw. großen Anlage mit Erweiterung bzw. Reduktion in Periode 2. Der erwartete Kapitalwert z.B. der Politik 2A und NT ergibt sich dabei aus: 0.4 [0.8 ċ (350) + 0.2 ċ (200)] + 0.6 [0.5 ċ (190) + 0.5 ċ (40)] = 197. Da die Anschaffung einer großen Anlage zum Zeitpunkt 0 und Behalten dieser Anlage in Periode 2 den höchsten erwarteten Kapitalwert verspricht, wäre diese Anlagenpolitik bei starrer Planung (auch mit Planrevision nach Periode 1) optimal im Sinne unseres Zielkriteriums. Anders geht die flexible Planung vor, denn hier werden zusätzlich zu den obigen Politiken auch noch bedingte Vorgehensweisen in Betracht gezogen. Da nach der ersten Periode bekannt ist, ob die Nachfrage in Periode 1 hoch oder niedrig war, verbessert sich der Informationsstand des Investors im Zeitablauf. Die flexible Planung bezieht dies ein, indem sie die Entscheidung der zweiten Periode davon abhängig macht, welches Niveau der Nachfrage (NF = H oder N) in Periode 1 beobachtet wurde. Damit stehen zusätzlich zu den obigen Politiken vier weitere zur Auswahl: A und [NT, wenn NF=H; 2A, wenn NF=N]; A und [2A, wenn NF=H; NT, wenn NF=N]; 2A und [A, wenn NF=H; NT, wenn NF=N]; 2A und [NT, wenn NF=H; A, wenn NF=N]. Die in den eckigen Klammern stehenden Teilpolitiken kennzeichnen dabei die durch die realisierte Nachfrage der Periode 1 bedingten Vorgehensweisen. So besagt z.B. die erste der obigen Politiken: Schaffe eine Anlage A in Periode 0 an; ist die Nachfrage in Periode 1 hoch, dann behalte A bei, ist die Nachfrage niedrig, erweitere auf 2A. Die optimale Anlagenpolitik bei der flexiblen Planung wird nun mithilfe des Roll back-Verfahrens ermittelt, das auf dem Optimalitätsprinzip von Bellman beruht. Wie bei der dynamischen Programmierung wird zunächst jene bedingt-optimale Teilpolitik ermittelt, wenn von den zeitlich zuletzt gelegenen Entscheidungsknoten ausgegangen wird (Schneeweiß, C.  1974; Schneeweiß, C.  1992). Dabei muss diese Teilpolitik in Abhängigkeit vom Umweltzustand (der Nachfrage) festgelegt werden. Im Entscheidungsbaum des obigen Beispiels sind die erwarteten Kapitalwerte für die Teilpolitiken an den Zufallsknoten in Periode 2 angegeben. So ergibt sich, z.B. ausgehend vom Entscheidungsknoten 1 bei NT (Beibehalten der Anlage A) ein erwarteter Kapitalwert von 190, bei 2A ein erwarteter Kapitalwert von 220. Damit wäre, unter der Bedingung, dass der Entscheidungsknoten 1 erreicht wird, die Entscheidung 2A optimal. Der Ast NT des Entscheidungsbaums kann gestrichen werden. Analog lassen sich die anderen bedingt-optimalen Entscheidungen ableiten und die jeweils anderen Äste des Entscheidungsbaums streichen. Damit fällt nun die Entscheidung zwischen der starren Politik 2A und NT (KW=197) und der flexiblen Politik A und [2A, wenn NF=H; NT, wenn NF=N]. Unter Bedachtnahme der bedingt-optimalen Teilpolitiken für Periode 2 lässt sich der erwartete Kapitalwert der flexiblen Politik ermitteln als 0.4 ċ (220) + 0.6 ċ (190) = 202. Da dieser höher ist als der erwartete Kapitalwert der starren Politik 2A und NT, fällt die Wahl zugunsten des flexiblen Plans aus. Der flexible Plan für den Investor sieht zunächst die Investition in eine kleine Anlage vor, wobei diese erweitert wird (A auf 2A), wenn die Nachfrage in Periode 1 hoch war. War die Nachfrage hingegen niedrig, dann wird nicht erweitert. Aus diesem Beispiel lässt sich auch ersehen, dass die flexible Planung einen höheren erwarteten Kapitalwert ergibt als die starre Planung. 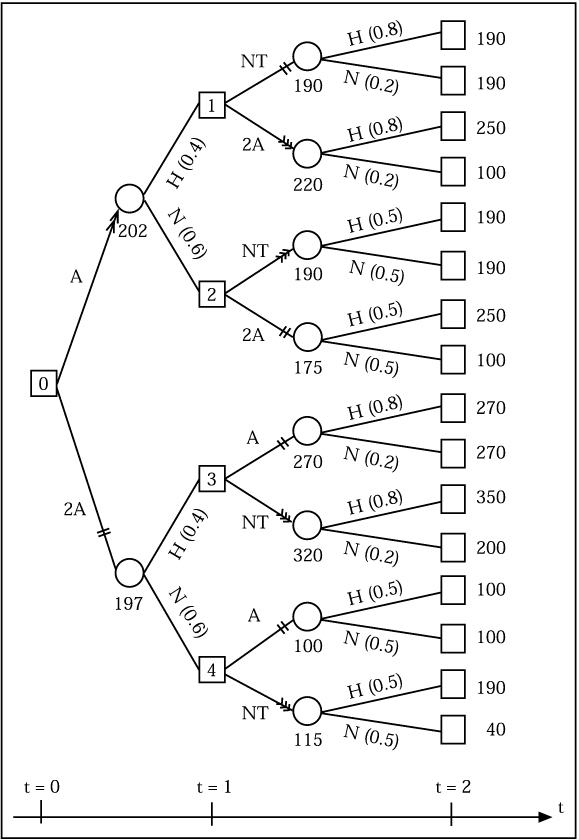Abb. 2: Entscheidungsbaum für die flexible Investitionsplanung 3. Ermittlung flexibler Pläne mit Hilfe stochastischer dynamischer Programmierung Lässt sich das Präferenzverhalten des Entscheidungsträgers durch ein Summenkriterium ausdrücken, dann können Mehrperiodenplanungen, bei denen explizit berücksichtigt wird, dass sich der Informationsstand bis zum Erreichen des Planungshorizonts verändert, auch mithilfe der stochastischen dynamischen Programmierung erfolgen (Schneeweiß, C.  1974; Schneeweiß, C.  1992; Inderfurth, K.  1982). Als Beurteilungsgröße unterschiedlicher Vorgehensweisen kann hier z.B. der Nutzenerwartungswert dienen, wobei die sog. Risikonutzenfunktion die Risikoeinstellung des Planungsträgers wiedergibt (Bamberg, G./Coenenberg, A.G.  1996). Von zentraler Bedeutung ist die Bellman\'sche Funktionalgleichung, die zur Ableitung von optimalen Politiken (flexiblen Plänen) herangezogen werden kann. Ebenso wie beim Entscheidungsbaum-Verfahren wird ein (stochastisches) dynamisches Programm in Rückwärtsrekursion gelöst, woraus sich jene Folge von bedingt-optimalen Anweisungen ergibt, die den größten Nutzenerwartungswert liefert. Während sich im deterministischen Fall mittels einer (an die Rückwärtsrekursion anschließenden) Vorwärtsrechnung eine Folge von optimalen Entscheidungen (unbedingten Empfehlungen) berechnen lässt, ist im stochastischen Fall eine solche Vorwärtsrechnung nicht möglich, da sich infolge der stochastischen Übergänge die optimale Vorgehensweise erst bei Realisierung der Zustände ergibt (Bamberg, G./Coenenberg, A.G.  1996). Die optimale Politik ergibt sich hier eben als eine Folge von flexiblen Eventualplänen, die Maßnahmen in Abhängigkeit vom eingetretenen Umweltzustand vorsehen. Für ein Beispiel sei verwiesen auf Schneeweiß (Schneeweiß, C.  1992, S. 109). IV. Realoptionen Der Schaffung und optimalen Ausnutzung von unternehmerischen Handlungsspielräumen kommt eine erhebliche Bedeutung zu, insbesondere dann, wenn Entscheidungen irreversibel sind und evtl. nicht sofort getroffen werden müssen, sondern der Entscheidungszeitpunkt aufgeschoben werden kann (Dixit, A.K./Pindyck, R.S.  1994). Die flexible Planung bezieht derartige Handlungsspielräume und die damit verbundene Flexibilität in die Modellierung explizit ein. Sie erkennt den Wert heutiger Maßnahmen, die Handlungsspielräume in der Zukunft eröffnen, und zeigt auf, dass es nicht sinnvoll ist, in der Gegenwart definitiv zu entscheiden, wie zukünftige Handlungsspielräume genutzt werden. So ist es in obigem Beispiel vorteilhaft, zunächst eine kleine Anlage anzuschaffen und die Erweiterungsentscheidung von der realisierten Nachfrage der Periode 1 abhängig zu machen. In neuerer Zeit ist eine Diskussion darüber entstanden, mit welchen Methoden derartige Handlungsspielräume bewertet werden sollten (Laux, C.  1993; Breuer, W./Gürtler, M./Schuhmacher, J.  1999; Crasselt, N./Tomaszewski, C.  1999). Grundsätzlich kann ein Marktwert für derartige Handlungsspielräume (Realoptionen) barwertorientiert oder optionspreistheoretisch fundiert ermittelt werden. Zwar lassen sich beide Methoden ökonomisch plausibel rechtfertigen, ohne zusätzliche Annahmen sind sie jedoch i.d.R. nicht äquivalent. Bei der barwertorientierten Ermittlung des Marktwertes einer Realoption wird der Barwert der Einzahlungsüberschüsse eines Investitionsprojekts ohne Realoption (z.B. erwarteter Kapitalwert bei sofortiger Investition) dem Barwert mit Realoption (z.B. erwarteter Kapitalwert bei Aufschub der Investition und optimaler Reaktion auf Nachfrage der Periode 1 wie bei flexibler Planung) gegenübergestellt, wobei die Differenz als Schätzwert für den Marktwert der Realoption dienen kann. Die Berechnung der jeweiligen Gegenwartswerte erfolgt, indem der entsprechende Erwartungswert der unsicheren Einzahlungsüberschüsse mit einem Kalkulationszinsfuß (der das Marktrisiko der Investition reflektiert) auf den Entscheidungszeitpunkt diskontiert wird. Das zentrale Problem der barwertorientierten Bewertung und damit der flexiblen Planung ist dabei, dass für unterschiedliche Formen der Ausnutzung der Handlungsspielräume (d.h. für verschiedene Risiken) eigentlich unterschiedliche Diskontsätze angesetzt werden müssten, die Ermittlung des risikoangepassten Diskontsatzes aber i.d.R. erhebliche Probleme bereitet (Trigeorgis, L.  1996). Die flexible Planung wird daher auch kritisch diskutiert (vgl. Crasselt, N./Tomaszewski, C.  1999; Laux, C.  1993). Bei der optionspreistheoretisch fundierten Ermittlung des Marktwertes einer Realoption wird versucht, den mit der Realoption verbundenen Zahlungsstrom durch ein Duplikationsportefeuille, das aus einer sicheren Anlage/Verschuldung und Teilen des Projektzahlungsstroms besteht, nachzubilden. Unter der Annahme der Arbitragefreiheit von Kapitalmärkten müssen sich die gleichen Preise für äquivalente Zahlungsreihen ergeben, und damit kann bei geeigneter Konstruktion des Portefeuilles eine Schätzung des Marktwerts der Realoption ermittelt werden. Wie Dangl und Kopel zeigen, führen die beiden obigen Bewertungsmethoden nur dann zu einem übereinstimmenden, eindeutigen Marktwert der Realoption, wenn der Zugang zu einem vollständigen Kapitalmarkt existiert (Dangl, T./Kopel, M.  2003). Nur in diesem Fall kann das unternehmerische Risiko durch ein Portefeuille von gehandelten Werten vollständig repliziert werden und die Bewertung ist unabhängig von der individuellen Zeit- und Risikopräferenz des Entscheidungsträgers. Ist der Markt jedoch unvollständig, dann ist die Ermittlung eines eindeutigen Marktwerts nicht mehr möglich. Mit Hilfe der Realoptionstheorie können dann bestenfalls Ober- und Untergrenzen für den Marktwert abgeleitet werden und damit ist auch die Investitionsentscheidung nicht mehr eindeutig vorgegeben. In diesem Fall liegt es an der Unternehmensleitung, die im Sinne des Unternehmensziels optimale Entscheidung festzulegen. Literatur: Bamberg, Günter/Coenenberg, Adolf G. : Betriebswirtschaftliche Entscheidungslehre, München, 9. A., 1996 Breuer, Wolfgang/Gürtler, Marc/Schuhmacher, Joachim : Die Bewertung betrieblicher Realoptionen, in: BFuP, 1999, S. 213 – 232 Crasselt, Nils/Tomaszewski, Claude : Realoptionen – Eine neue Methode der Investitionsrechnung?, in: WiSt, 1999, S. 556 – 559 Dangl, Thomas/Kopel, Michael : Die Bedeutung vollständiger Finanzmärkte für die Anwendung des Realoptionsansatzes, in: Reale Optionen – Konzepte, Praxis und Perspektiven strategischer Unternehmensfinanzierung, hrsg. v. Hommel, Ulrich/Scholich, Martin/Baecker, Philipp, Berlin et al. 2003, S. 37 – 62 Dinkelbach, Werner : Flexible Planung, in: HWPlan, hrsg. v. Szyperski, Norbert, Stuttgart 1989, S. Sp. 507 – 512 Dixit, Avinash K./Pindyck, Robert S. : Investment Under Uncertainty, Princeton 1994 Franke, Günter/Hax, Herbert : Finanzwirtschaft des Unternehmens und Kapitalmarkt, Berlin et al., 4. A., 1999 Hax, Herbert : Investitionstheorie, Würzburg et al., 5. A., 1993 Inderfurth, Karl : Starre und flexible Investitionsplanung, Wiesbaden 1982 Kruschwitz, Lutz : Investitionsrechnung, München, 7. A., 1998 Laux, Christian : Handlungsspielräume im Leistungsbereich des Unternehmens: Eine Anwendung der Optionspreistheorie, in: ZfbF, Jg. 45, 1993, S. 933 – 958 Ossadnik, Wolfgang : Planung und Entscheidung, in: Betriebswirtschaftslehre, hrsg. v. Corsten, Hans/Reiß, Michael, München 1994, S. 141 – 232 Schneeweiß, Christoph : Planung, Bd. 2, Berlin et al. 1992 Schneeweiß, Christoph : Dynamisches Programmieren, Würzburg et al. 1974 Trigeorgis, Lenos : Real Options, Cambridge 1996