|
Investitionsplanung
Inhaltsübersicht
I. Anliegen der Investitionsplanung
II. Planung einzelner Investitionsvorhaben
III. Investitionsprogrammplanung
I. Anliegen der Investitionsplanung
Investitionsplanung kann als zielgerichtete und systematische Auseinandersetzung mit den (voraussichtlichen) Konsequenzen von Investitionen aufgefasst werden. Vornehmlich ist hierbei an folgende Aspekte zu denken:
| - | Aus leistungswirtschaftlicher Sicht legen Realinvestitionen (insbes. Sachinvestitionen) quantitative und qualitative Kapazitäten fest, fixieren auf diese Weise die Kosten- und Erlösstruktur einer Unternehmung. Bleiben die Erlöse hinter den Erwartungen zurück und lässt sich die Anschaffungsausgabe durch Liquidation des Investitionsobjektes nicht vollständig wiedergewinnen ( „ irreversible Investition “ ), entstehen sunk costs, welche künftig die Entscheidungsflexiblität beschränken (Krahnen, J.P. 1991). | | - | Finanzwirtschaftlich interessieren Höhe und zeitlicher Anfall der mit Investitionen erzielbaren Gewinne bzw. Verluste sowie die hierbei gebundene Liquidität. Während erstere unter Zuhilfenahme von Investitionsrechenverfahren festgestellt werden, dient die Finanzplanung als Perioden- oder Projektplanung zur Steuerung der Liquidität. | | - | Aus personalwirtschaftlicher Perspektive sind Motivation und Anreizwirkungen von Investitionen von Bedeutung sowie gegebenenfalls gewisse kapazitative und organisatorische Festlegungen (beispielsweise Art der Arbeitsteilung oder der kommunikativen Vernetzung). | | - | Schließlich müssen die informationswirtschaftlichen Folgen einer bestimmten Investitionspolitik bedacht werden. Abgesehen davon, dass z.B. Bauinvestitionen per se sichtbare Zeichen für die unternehmungsinterne und -externe Öffentlichkeit setzen, ist hier ihr Niederschlag in Publikationsrechnungen anzuführen: Bilanzstrukturen und Kapitalflüsse dienen in hohem Maße der Rechenschaftslegung und münden letztlich in eine Erfolgs- und Liquiditätsanalyse als Resultat der Investitionstätigkeit. |
Als Charakteristikum für Investitionen lässt sich die für eine gewisse Zeitdauer eingegangene Kapitalbindung herausstellen. Dies beinhaltet, dass für die Beurteilung von Investitionen deren finanzielle Konsequenzen im Mittelpunkt der Investitionsplanung stehen. Folgerichtig sind Investitionen als Entscheidung über Ausgaben zur Erlangung von Wirtschaftsgütern definierbar, wobei erwerbswirtschaftliche Investitionen zudem – und vor allem – der Einnahmenerzielung dienen, mithin dem Kriterium der Vorteilhaftigkeit zu genügen haben, das sich als Gewinn- oder Rentabilitätskennziffer quantifizieren lässt.
II. Planung einzelner Investitionsvorhaben
1. Projektplanung
Dem Prinzip sukzessiver Planung folgend, beschränkt sich die Projektplanung auf isolierte Investitionsvorhaben, ohne die Wechselwirkung zu anderen oder nachfolgenden Maßnahmen zu berücksichtigen. Relevant für die Projektbeurteilung sind dann genau diejenigen finanziellen Konsequenzen in Form von Ausgaben (Auszahlungen) und Einnahmen (Einzahlungen), die durch die Entscheidung für das Investitionsvorhaben ausgelöst werden. Neben dem Investitionsobjekt i. eng. S., das bilanziell oft dem Anlagevermögen zuzuordnen ist, sind auch einhergehende zahlungswirksame Folgen im Umlaufvermögen sowie weitere Zahlungen beispielsweise für Personalausgaben eingeschlossen. Darüber hinaus zwingt die Zeitverschiedenheit aller Geldzu- und -abflüsse zur Berücksichtigung temporärer Wiederanlagen von Einnahmenüberschüssen und Finanzierung von Ausgabenfehlbeträgen, die sich in entsprechenden Zinsfüßen ausdrücken lassen und letztlich die Aggregation aller Einnahmen und Ausgaben zu einer einheitlichen, die (Un-)Vorteilhaftigkeit eines Projektes zum Ausdruck bringenden Maßgröße erlauben.
Als optimaler Zeitpunkt für die Realisierung eines Investitionsprojektes lässt sich derjenige ansehen, welcher hinsichtlich des gewählten Vorteilskriteriums (z.B. Kapitalwert, Rentabilität) am besten abschneidet. Hierbei wird unterstellt, dass die Zahlungsfolge, welche die Investition charakterisiert, mit dem Beginn der Projektperiode variiert. Dies kann in steuerlichen Änderungen – wie dem Beginn bzw. Auslaufen bestimmter steuerlicher Förderungen oder Belastungen – genauso begründet sein wie in gewissen marktlichen Reaktionen auf ein Vorhaben, beispielsweise ein sich veränderndes Nachfrageverhalten von Kunden oder Auswirkungen von Aktionen der Konkurrenz. In Verbindung mit der Projektdurchführung(splanung) entstehen hier oftmals zeitlich-abwicklungstechnische Probleme (z.B. bei Bauinvestitionen), deren Bewältigung die Vorteilhaftigkeit nachhaltig zu beeinflussen vermag.
2. Optimale Investitionsdauer
Bei Sachinvestitionen (z.B. Fahrzeuge, Maschinen, Gebäude) wie auch bei Rechten oder Finanzinvestitionen (z.B. Wertpapiere) stellt sich oftmals die Frage, wie lange diese zweckmäßigerweise genutzt resp. gehalten werden sollen. Innerhalb technisch oder rechtlich bedingter Grenzen kann nämlich die wirtschaftlich optimale Dauer einer Investition sehr wohl variieren. Ausgehend vom Beginn des Projektes ist eine Fortführung so lange angeraten, wie sich der Gewinn noch steigern lässt. Derartige zeitliche Grenzgewinne ΔGt zwischen zwei Zeitpunkten (t – 1) und t lassen sich mit Hilfe folgender Formel bestimmen und auf ihre Einflussfaktoren zurückführen:
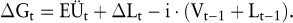
| - | EÜt beziffert hierbei den Ertragsüberschuss, der bei Weiterführung der Investition in der Periode zwischen (t – 1) und t erwirtschaftet wird. Im Einzelnen setzt er sich zusammen aus den anfallenden Projekteinnahmen Et, vermehrt um eventuelle Zinserträge aus temporären Wiederanlagen gerade nicht benötigter Liquidität und vermindert um die Projektausgaben At unter Einschluss der Finanzierungskosten dieser Investition. Beispielsweise betrage EÜ2 bei einer Investition I 180 Geldeinheiten, die sich aus E2 = 205 vermindert um Zinsaufwendungen von 25 zusammensetzen. | | - | Die Veränderung des Liquidations- oder Veräußerungserlöses von (t – 1) auf t sei mit ΔLt bezeichnet. Bei Sachinvestitionen ist ΔLt in der Regel negativ, da bei längerer Nutzung der Liquidationserlös sinkt, etwa bei dem Beispielprojekt I um 150 Geldeinheiten. | | - | Schließlich gehen bei Fortführung der Investition diejenigen Zinserträge verloren, welche bei ihrem Abbruch in (t – 1) und Reinvestition dieses Überschusses hätten erlöst werden können. Deren Höhe hängt ab vom Zinssatz i, der mit dem bis zum Zeitpunkt (t – 1) erwirtschafteten Investitionsgewinn (bzw. -verlust) Vt – 1 zuzüglich des Liquidations-/Veräußerungserlöses Lt – 1 zu gewichten ist. Bei Projekt I betrage V1 = – 250 und L1 = 350, sodass bei einem Zinsfuß von 10% bei Fortsetzung der Investition Zinserträge in Höhe von 10 verlorengehen. Zusammengefasst mit dem Ertragsüberschuss von 180 und der Verminderung des Liquidationserlöses um 150 resultiert ein zeitlicher Grenzgewinn ΔG2 = + 20, die Weiterführung von Projekt I ist also vorteilhaft (s. auch Abb. 1 unten). |
Ein an zeitlichen Grenzgewinnen orientiertes Abbruchkriterium ist dann anwendbar, wenn Gewinne und Verluste nicht im Wechsel auftreten. Andernfalls muss für jeden Zeitpunkt t das Vorteilskriterium (z.B. der Kapital- oder Vermögensendwert) ermittelt und hieraus der bestmögliche Wert ausgewählt werden. Des Weiteren sind Ertragsteuern dann zu berücksichtigen, wenn sie die optimale Investitionsdauer – beispielsweise wegen degressiver Abschreibung oder Absetzbarkeit von Darlehnszinsen – beeinflussen.
3. Investitionsketten
Eine Folge von Investitionsprojekten wird als Investitionskette bezeichnet. Durch die Aneinanderreihung von – abgeschlossenen oder abgebrochenen – Einzelinvestitionen wird ggf. nicht nur der Planungshorizont weiter in die Zukunft verschoben, sondern auch durch geschickte Terminierung und Auswahl der Folgeprojekte eine optimale Investitionsstrategie möglich. Eine solche zeitlich-simultane Planung kann entweder das jeweils nachfolgende Projekt vom Eintritt bestimmter Ereignisse abhängig machen oder a priori eine Projektreihenfolge fixieren ( „ starre Planung “ ). Letzteres ist in Abb. 1 für einen Planungszeitraum von drei Perioden exemplarisch dargelegt:
| - | Im Zeitpunkt t = 0 kann entweder Projekt I realisiert werden oder nicht ( „ Null-Alternative “ ). | | - | In t = 1 bestehen die Möglichkeiten der Weiterführung von Projekt I, die Aufnahme von Projekt II oder die Null-Alternative. | | - | Schließlich können in t = 2 zuvor angefangene Projekte fortgesetzt, Projekt III begonnen oder die Null-Alternative verwirklicht werden. |
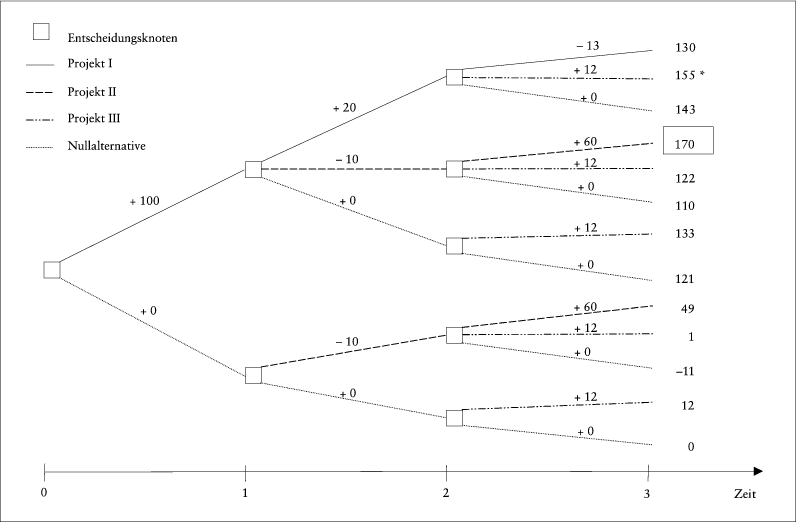
Abb. 1: Endliche Investitionsketten
Soweit die zeitlichen Grenzgewinne bzw. -verluste bekannt sind, kann hieraus der jeweilige Investitionsgewinn Vn, der Vermögensendwert (Schirmeister, R. 1990, S. 35 ff.), jeder Strategie für das Ende des Planungszeitraumes über die Formel
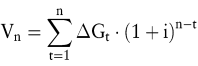
errechnet werden. Im Beispiel der Abb. 1 sind für i = 10 % die Investitionsgewinne in n = 3 angegeben: Optimal ist mit V3 = 170 (= 100 · 1,12 – 10 · 1,1 + 60) offensichtlich die Strategie, zunächst Projekt I zu realisieren und es in t = 1 durch Projekt II zu ersetzen. Diese durch vollständige Enumeration gefundene Lösung ist bei endlichen Investitionsketten stets ermittelbar, mit zunehmender Anzahl an Perioden und Projekten allerdings rasch aufwendig. Heuristische Lösungsverfahren, wie beispielsweise das Kriterium des jeweils höchsten zeitlichen Grenzgewinns ( „ bester Nachfolger “ ), garantieren hingegen nicht notwendigerweise die vorteilhafteste Strategie; im Beispiel hieße das, Projekt I bis t = 2 zu belassen und anschließend zu Projekt III zu wechseln, wobei der Gesamtgewinn V3 = 155 zwar beachtlich, aber eben nicht maximal ist.
Ein Anwendungsfall endlicher Investitionsketten ist das Ersatzproblem: Während bislang eine Planung im Zeitpunkt t = 0 angenommen wurde, stellt sich die Frage nach der optimalen Nutzungsdauer und ggf. einem Ersatz bei einem laufenden Investitionsvorhaben möglicherweise erneut, wenn sich die Informationen gegenüber der originären Entscheidungsfindung geändert haben. Gründe hierfür können im Datenrahmen (z.B. andere Preise) oder im Entscheidungsfeld selbst liegen. Bei Letzterem ist an neue Handlungsalternativen (wie technische Innovationen bei Sachgütern, neue Finanzanlagen) genauso zu denken wie an Nachfrage- oder Wettbewerbsverschiebungen, die zu neuen Planungsrechnungen auf der Basis anderer Zahlungsströme zwingen.
Ein vielfach diskutiertes Problem ist das identischer Investitionsketten, also Folgen von Investitionen, bei welchen die einzelnen Kettenglieder identische Zahlungsreihen aufweisen oder zumindest in Bezug auf ein Vorteilskriterium (i.d.R. auf den Kapitalwert) übereinstimmen. Im Falle einer endlichen Kette, deren Realitätsbezug allerdings offen bleibt, verlängert sich die optimale Nutzungsdauer mit jedem Folgeprojekt ( „ Ketteneffekt “ ). Bei unendlich identischen Investitionsketten, die mangels Planbarkeit gerne bei einer Unternehmung auf Dauer unterstellt werden, braucht die optimale Nutzungsdauer nicht mit derjenigen übereinzustimmen, die bei isolierter Projektbetrachtung als vorteilhaft bestimmt wird (als Überblick Götze, U./Bloech, J. 2006, S. 235 ff.; Kruschwitz, L. 2005, S. 207 ff.).
III. Investitionsprogrammplanung
Ein Investitions-Finanzierungs-Programm ( „ Kapitalbudget “ ) besteht aus voneinander unabhängigen Investitionsprojekten, die, finanziert durch voneinander unabhängige Finanzierungsprojekte, ein vorgegebenes Gewinnziel am besten erfüllen.
1. Ein-Perioden-Modell
Der einfachste Fall des Kapitalbudgets, das auf die Zeitspanne zwischen t = 0 und t = 1 beschränkte Dean-Modell (Dean, J. 1969), geht von einem unvollkommenen Kapitalmarkt aus, auf welchem die Kapitalaufnahme zu bestimmten Konditionen beschränkt ist. Einander gegenübergestellt werden die nach ihrer absteigenden Rentabilität geordneten Investitionsprojekte IPj, die Kapitalnachfragefunktion, und die nach ihren aufsteigenden relativen Finanzierungskosten geordneten Finanzierungsprojekte FPk, die Kapitalangebotsfunktion (vgl. exemplarisch Abb. 2).
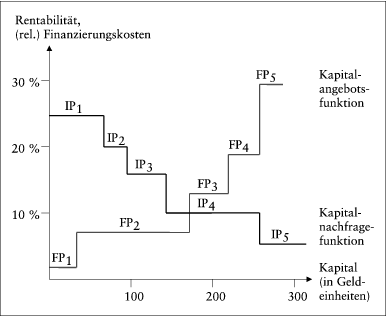
Abb. 2: Dean-Modell
Optimal im Sinne der Zielsetzung eines maximalen Vermögensendwertes in t = 1 ist dann dasjenige Programm, welches alle Investitionsprojekte mit einer Rentabilität größer/gleich derjenigen des Schnittpunktes von Kapitalnachfrage- und -angebotsfunktion enthält. Diese werden genau mit denjenigen Finanzierungsmöglichkeiten realisiert, deren relative Finanzierungskosten (= interne Verzinsung) kleiner/gleich derjenigen des Schnittpunktes sind. Dieser Schnittpunkt kann als modellendogener Kalkulationszinsfuß interpretiert werden, da alle im optimalen Programm enthaltenen Projekte einen Kapitalwert größer/gleich null aufweisen, alle nicht im optimalen Programm enthaltenen Projekte einen negativen Kapitalwert. Als endogener Parameter ist dieser Kalkulationszinsfuß allerdings ex ante nicht bekannt, sodass auf die Aufstellung des Modells nicht verzichtet werden kann.
Bei aller Begrenztheit – nämlich auf eine Periode und die Unabhängigkeit der Finanzierungsalternativen von der Realisierung bestimmter Investitionsprojekte – zeichnet sich das Dean-Modell durch seinen hohen heuristischen Gehalt aus, der die Intention der Programmplanung einprägsam widerspiegelt.
2. Mehr-Perioden-Modelle
Ein Kapitalbudget für mehrere Perioden hat zwei Anforderungen zu erfüllen:
| - | In jedem Zeitpunkt t = 0, 1, ..., n muss die Liquidität gesichert sein; d.h., der Saldo aller Einnahmen (aus Investitionsrückflüssen, Kapitalaufnahmen, Zinserträgen) und Ausgaben (für Investitionen, Kapitaldienste) darf nie negativ werden. | | - | Die Zusammensetzung des Kapitalbudgets bestimmt sich nach der gewählten erfolgswirtschaftlichen Zielsetzung. Analog zum Ein-Perioden-Modell kann diese beispielsweise in der Maximierung des Vermögensendwertes Vn am Ende des Planungszeitraumes bestehen. |
Das folgende Beispiel eines 2-Perioden-Modells möge die Idee der Programmplanung verdeutlichen: Vorgesehen seien die beiden Investitionsprojekte IPI mit A0 = 200, E1 = 170, E2 = 118 und IPII mit A0 = 100, E1 = 52, E2 = 69, die höchstens einmal (xI, xII ≤ 1) realisiert werden sollen. Zur Finanzierung stehen ein Kredit FPI über E0 = 200 zu 5 % und ein weiterer Kredit FPIII über 100 zu 12 % zur Verfügung; beide Kredite müssen nicht ausgeschöpft werden (d.h. yI, yIII ≤ 1), sind zu jedem Termin rückzahlbar und bei laufender Zinszahlung endfällig zu tilgen. Soweit sich in t = 1 Einnahmenüberschüsse ergeben, werden sie während der ersten Periode in der Kasse gehalten, während der zweiten als Finanzanlage zu einem Habenzinsfuß von 3 % angelegt. Der angestrebte maximale Vermögensendwert V2 wird nun über ein (lineares) Optimalmodell ermittelt. In die Liquiditätsrestriktionen
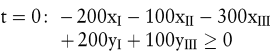
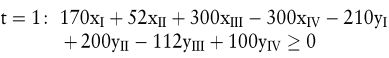
gehen zunächst die Zahlungen der beiden Investitionsprojekte, gewichtet mit ihren Wiederholungsfaktoren xI bzw. xII ein. Die Variablen xIII bzw. xIV bezeichnen die Möglichkeit zur Kassenhaltung bzw. Finanzanlage in der ersten resp. zweiten Periode, während yI und yIII die Darlehensaufnahmen symbolisieren. Die Kreditkündigung wird durch die Zerlegung in jeweils einperiodige Kreditlaufzeiten erfasst, wozu die (Hilfs-)Variablen yII und yIV eingeführt werden; Zinsaufwendungen sind explizit als Zahlungsgrößen ausgewiesen (z.B. bedeutet – 210y1 in t = 1, dass der Kredit FPI = 200 getilgt und zu 5 % verzinst wird, was insgesamt eine Ausgabe von 210 nach sich zieht). In den Projektmengenrestriktionen
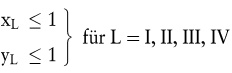
wird festgelegt, wie oft das einzelne Projekt realisiert werden kann, wobei ggf. auch Teilbarkeits- (z.B. yI ∊ [0,1] oder Ganzzahligkeitsbedingungen (z.B. xI = 0 oder 1) Verwendung finden können. Die Zielsetzung des maximalen Vermögensendwertes V2 findet sich in der Zielfunktion
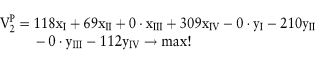
Analog zu den Liquiditätsrestriktionen sind alle Investitions- und Finanzierungsprojekte sowie sämtliche Zinsen explizit erfasst. Unter Beachtung der Nichtnegativitätsbedingungen
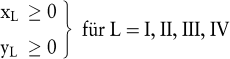
errechnet sich mittels eines geeigneten (Simplex-)Algorithmus ein maximaler Vermögensendwert V2 = 82. Dieser wird erreicht, indem beide Investitionen durchgeführt werden (xI = xII = 1), Einnahmenüberschüsse nicht anfallen (xIII = xIV = 0), beide Darlehen in der ersten Periode voll ausgeschöpft werden (yI = yIII = 1), in der zweiten Periode hingegen auf FPIII verzichtet (yIV = 0) und FPI lediglich noch zur Hälfte in Anspruch genommen wird (yII = 0,5).
Allgemein stellt sich ein derartiges „ Investions-Finanzierungs-Programm “ als ein (lineares) Optimalmodell dar, bestehend aus Zielfunktion und Restriktionen. Neben dem Vermögensstreben, operationalisiert etwa im Vermögensendwert Vn, können auch periodisch konstante Entnahmen als Ziel verfolgt werden. Die Einbeziehung von (Ertrag-)Steuern, die prinzipiell geboten ist, wird allerdings mit erhöhter, der informatorischen Fundierung und der rechnerischen Bewältigung zuwiderlaufender Komplexität erkauft. Neben den Liquiditäts- und Projektmengenrestriktionen, ergänzt um die Nichtnegativitätsbedingungen, sind auch Ausweitungen auf andere Unternehmungsbereiche – wie Produktions-, Absatz-, Personalrestriktionen – genauso möglich wie die Einbindung von Wahrscheinlichkeitsverteilungen gewisser Parameter (als Überblick Hax, H. 1985, S. 62 ff.; Kruschwitz, L. 2005, S. 222 ff.).
Die Schwierigkeiten der Implementierung von Optimierungsmodellen in der Unternehmungspraxis bestehen einmal in der zeitnahen Bereitstellung der erforderlichen Plandaten. Mit einem ausgebauten, auf Zahlungsgrößen basierenden Rechnungswesen wäre dies im Prinzip realisierbar, wobei die nicht unerheblichen Kosten dem Nutzen gegenüberstehen. Zum anderen ist der Ansatz, durch die steigende Anzahl und Genauigkeit der zu erfassenden interdependenten Wirkungen, insbesondere wenn hierbei an Marktstrukturen gedacht wird, konzeptionell begrenzt, weil dadurch Entscheidungen letztlich überflüssig werden. Hinsichtlich der Modellausgestaltung bietet es sich daher an, entweder eine Beschränkung auf Teilprobleme zu forcieren (wie etwa die Liquiditätssteuerung in Verbindung mit der Disposition kurzfristiger Finanzanlagen) oder sich auf wesentliche Grundstrukturen ( „ robuste Schritte “ ) zu konzentrieren.
3. Budgetplanung
Die Praxis der Investitionsprogrammplanung verzichtet weitgehend auf Unterstützung durch Optimalmodelle, orientiert sich eher, wenn auch nicht immer explizit genannt, an dem Dean-Modell. Die zumeist im Jahresrhythmus durchgeführte zentrale Koordination der dezentral eruierten Projektvorschläge an insbes. Sachinvestitionen trifft die zu realisierende Auswahl anhand unternehmungsüblicher Vorteilskriterien (z.B. Rentabilität, Kapital- oder Endwert, Amortisationsperiode), ergänzt um Risikogesichtspunkte und qualitative Aspekte, welche die eingangs aufgeführten Konsequenzen von Investitionen graduell unterschiedlich und unternehmungsspezifisch beachten (beispielsweise strategisch-leistungswirtschaftliche Wirkungen, Bilanzwirkung). Die Finanzierung erfolgt typischerweise organisatorisch und sachlich getrennt von der Investitionsprogrammplanung und erscheint als verfügbares Kapitalvolumen. Bei besonders attraktiven Investitionsvorhaben wird allerdings die Finanzierung selbst hinterfragt und ggf. zusätzliches projektbezogenes Kapital beschafft. Völlig getrennt hiervon erfolgt die Planung von Finanzanlagen, die entweder unternehmungspolitisch motiviert die Auswahl trifft (z.B. Beteiligungserwerb) oder anhand einer Rendite-Risiko-Mischung ( „ Portfolio-Selection “ ) vorgeht.
Literatur:
Dean, Joel : Capital Budgeting, New York et al., 8. A., 1969
Götze, Uwe/Bloech, Jürgen : Investitionsrechnung, Berlin et al., 5. A., 2006
Hax, Herbert : Investitionstheorie, Würzburg et al., 5. A., 1985
Krahnen, Jan Pieter : Sunk Costs und Unternehmensfinanzierung, Wiesbaden 1991
Kruschwitz, Lutz : Investitionsrechnung, München et al., 10. A., 2005
Matschke, Manfred Jürgen : Investitionsplanung und Investitionskontrolle, Herne et al., 1993
Schirmeister, Raimund : Investitionsrechnung (Hörbuch), Bremen 2005
Schirmeister, Raimund : Theorie finanzmathematischer Investitionsrechnungen bei unvolkkommenem Kapitalmarkt, München 1990
Schneider, Dieter : Investition, Finanzierung und Besteuerung, Wiesbaden, 7. A., 1992
|