Induktive Statistik

siehe unter Analytische Statistik siehe unter Beurteilende Statistik siehe unter Inferenzstatistik siehe unter Schließende Statistik Die I. ist die Lehre von Grundlagen und Methoden, nach denen Schlüsse von einer Stichprobe auf eine Grundgesamtheit bzw. von einzelnen Beobachtungen auf eine sie hervorrufende Gesetzmäßigkeit gezogen werden. In derartigen induktiven Schlüssen geht die Conclusio (die resultierende Aussage) über die Prämisse (die Stichprobe bzw. Beobachtungen) hinaus; daher können solche Schlüsse notwendigerweise nur mit einer mehr oder weniger großen Sicherheit zutreffen. Die für jede Induktionstheorie zentrale Frage lautet: Wie wird der Sicherheitsgrad induktiver Schlüsse gemessen? Dieses Problem, das meistens in engen Zusammenhang mit der Wahrscheinlichkeitstheorie (Wahrscheinlichkeitsrechnung) gebracht wird, besitzt die verschiedensten Lösungen und Lösungsversuche. Auch innerhalb der I. gibt es auf diese Frage verschiedene Antworten, die zu unterschiedlichen Grundlagenkonzepten der I. führen; darunter sind die wichtigsten: die klassische Inferenz, die Likelihood-Inferenz, die Bayes-Inferenz und die Statistische Entscheidungstheorie. Ihr gemeinsamer Kern besteht aus folgendem Modell. Das Grundmodell der I. Jedem statistischen Schluß liegen Beobachtungen x1, ..., xn (zusammenfassend Stichprobe genannt) eines Untersuchungsmerkmals X zugrunde, das als Zufallsgröße aufgefaßt wird. Die Verteilung  von X (Verteilung von X in der Grundgesamtheit) ist nicht oder nicht vollständig bekannt. Aufgrund der vorliegenden Beobachtungen sollen Aussagen über diese Verteilung getroffen werden (Schluß von der Stichprobe auf die Grundgesamtheit). Vor den Beobachtungen bereits vorhandene Vorkenntnisse über X werden in einer Verteilungsannahme wiedergegeben, indem eine Menge W der für X in Betracht kommenden Verteilungen festgelegt wird. Je größer W ist, desto geringer sind die Vorkenntnisse über X. Man kann davon ausgehen, daß die Verteilungen in W entweder sämtlich diskret oder sämtlich stetig sind. Unter einer parametrischen Verteilungsannahme, die wir hier zugrunde legen wollen, läßt sich W darstellen als
(1)     W = {h (x; q) ; q Î Q Dabei ist q ein (ein- oder mehrdimensionaler) unbekannter Verteilungsparameter (Parameter der Grundgesamtheit), Q der dazugehörige Parameterraum (das ist der Bereich der möglichen Werte von q) und h (x; q) die Wahrscheinlichkeitsfunktion (im diskreten Fall) bzw. die Dichte (im stetigen Fall) von X in Abhängigkeit von q. Die Stichprobe x1, ..., xn, bestehend aus n Realisationen von X, läßt sich auch als eine Realisation von n Zufallsgrößen X1, ..., Xn, den Stichprobenvariablen, auffassen: Xi gibt an, welcher Wert von X beim i-ten Versuch (am i-ten Merkmalsträger in der Auswahl) beobachtet werden wird. Die gemeinsame Verteilung der X1, ..., Xn, die sogenannte Stichprobenverteilung, hängt dann ebenfalls von q ab; ihre Wahrscheinlichkeitsfunktion bzw. Dichte bezeichnen wir mit f(x1, ..., xn; q). Die Situation vor der Beobachtung wird durch die Stichprobenverteilung, die Situation danach durch die beobachteten Werte x1, ..., xn beschrieben. Aus der Stichprobe soll auf den Wert von q geschlossen oder allgemein eine Aussage über q gewonnen werden. Um die Unsicherheit dieses Schlusses quantifizieren zu können, muß die Stichprobe zufällig  zustande gekommen sein, daß heißt: für jedes q muß f(x1, ..., xn; q) aus h (x; q) eindeutig bestimmt werden können. Auf diese Weise wird durch
(1) auch die Menge der zugelassenen Stichprobenverteilungen
(2)     Wn = {f(x1, ..., xn; q) : q Î Q} festgelegt. Im einfachsten Fall ergibt sich die Stichprobe aus unabhängigen Versuchswiederholungen: X1, ..., Xn sind dann unabhängige Zufallsgrößen, die alle dieselbe Verteilung wie X besitzen. Die Stichprobenverteilung ergibt sich daraus als
(3)     f(x1, ..., xn; q) = h (x1; q) * ... * h (xn; q) Klassische Inferenz. Charakteristisch für die klassische Inferenz ist zunächst einmal ihr objektivistischer Standpunkt: Der induktive Schluß, insbesondere die Beurteilung seines Sicherheitsgrades soll frei von subjektiven Einflüssen sein. Entsprechend gehen die Vertreter dieses Standpunktes, die Objektivisten, von einem objektivistischen Wahrscheinlichkeitsbegriff aus, nach dem die Wahrscheinlichkeit P(A) eines Ereignisses A einen objektiven, vom jeweiligen Betrachter unabhängigen Wert darstellt. P(A) kann näherungsweise bestimmt werden durch die relative Häufigkeit, mit der A unter n unabhängigen Versuchswiederholungen eintritt, wenn n hinreichend groß ist (Gesetz der großen Zahlen, Häufigkeitsinterpretation der Wahrscheinlichkeit). Streng genommen ordnen daher Objektivisten nur solchen Größen Wahrscheinlichkeiten zu, die sich in sehr oft wiederholbaren Versuchen beobachten lassen. Damit verbunden ist eine prinzipielle Trennung zwischen zufälligen und nichtzufälligen Größen. Der unbekannte Parameter q wird als eine feste, nichtzufällige Größe angesehen, die Stichprobe als zufallsabhängig. Daraus ergibt sich das zweite wesentliche Element der klassischen Inferenz: Vor der Beobachtung der Stichprobe (a priori) wird keine Bewertung der möglichen Parameterwerte etwa in Form einer Wahrscheinlichkeitsverteilung auf dem Parameterraum (a priori Verteilung) vorgenommen. Die klassische Inferenz arbeitet ohne a priori Verteilungen. Das dritte charakteristische Element klassischer Inferenz besteht in einer frequentistischen Beurteilung des Sicherheitsgrades eines induktiven Schlusses: Wie sicher ein Schluß von einer Stichprobe auf die Grundgesamtheit ist, wird daran gemessen, wie oft man bei häufiger Beobachtung einer Stichprobe mit dem betreffenden Schluß zu einer richtigen Aussage gelangt. In der klassischen Inferenz wird daher nicht nur die eine beobachtete Stichprobe berücksichtigt, sondern auch nach der Beobachtung noch alle möglichen, aber nicht beobachteten Stichproben und deren Wahrscheinlichkeiten (die Stichprobenverteilung). Wird dabei der Sicherheitsgrad des Schlusses unmittelbar durch die Wahrscheinlichkeit ausgedrückt, mit der er zu richtigen Aussagen führt, so stimmt die frequentistische Beurteilung mit der Häufigkeitsinterpretation der Wahrscheinlichkeit überein und ergibt sich damit notwendigerweise aus dem objektivistischen Wahrscheinlichkeitsbegriff. Die wichtigsten Verfahren der klassischen Inferenz sind Punktschätzungen (Schätzverfahren), Intervallschätzungen (Konfidenzintervalle; Konfidenz) und Tests (Signifikanztests). Likelihood-Inferenz. Dreh- und Angelpunkt der Likelihood-Inferenz ist die konsequente Unterscheidung zwischen der Situation vor der Beobachtung der Stichprobe und der Situation danach. Vor der Beobachtung legt f(x1, ..., xn; q) wie in der klassischen Inferenz die Stichprobenverteilung fest; nach der Beobachtung wird f(x1, ..., xn; q) als Funktion von q bei gegebenen x1, ..., xn aufgefaßt, man nennt sie die Likelihood-Funktion nach der Beobachtung; Schreibweise:
(4)     lik (q; x1, ..., xn) = f(x1, ..., xn; q) Diese Funktion gibt für jeden q-Wert ein Maß dafür an, wie wahrscheinlich es war, die Stichprobe zu beobachten, wenn q zugrunde liegt. Die Funktionswerte werden als Likelihood ("Plausibilität") von q aufgrund der Beobachtung x1, ..., xn aufgefaßt. Die beiden folgenden Postulate  zusammenfassend das Likelihood-Prinzip genannt  bilden die Grundlage der Likelihood-Inferenz:          1)         Die Likelihood-Funktion enthält die gesamte in der Beobachtung vorhandene Information über q.          2)         Ein Parameterwert q1 ist aufgrund der Beobachtung plausibler oder glaubwürdiger als ein Parameter q2, wenn die Likelihood von q1 größer ist als diejenige von q2. Man erkennt den nichtfrequentistischen Charakter der Likelihood-Inferenz: Nach der Beobachtung spielt es für die Beurteilung eines Schlusses keine Rolle mehr, was für Stichproben sonst noch hätten beobachtet werden können. In den beiden anderen Charakteristika stimmt die Likelihood-Inferenz mit der klassischen Inferenz überein: Wie jene vertritt sie einen objektivistischen Standpunkt und arbeitet ohne a priori Verteilungen auf dem Parameterraum. Als Inferenzarten kommen wieder Punktschätzungen (Maximum-Likelihood-Methode), Intervallschätzungen (Likelihood-Intervalle, die alle jene Parameterwerte enthalten, deren Likelihood mindestens gleich einem vorgegebenen g ist) und Tests (Likelihood-Quotienten-Tests) in Betracht. Schätzungen und Tests der Likelihood-Inferenz sind oft auch aus klassischer Sicht optimal oder nahezu optimal, so daß mit dem Likelihood-Prinzip auch in der klassischen Inferenz argumentiert wird. Bayes-Inferenz. Das eigentliche Gegenstück zur klassischen Inferenz ist die Bayes-Inferenz: Sie ist subjektivistisch orientiert, arbeitet mit a priori Verteilungen auf dem Parameterraum und wendet eine nichtfrequentistische Betrachtungsweise an. Die Vertreter eines subjektivistischen Standpunktes, die Subjektivisten, gehen davon aus, daß Wahrscheinlichkeiten vom jeweiligen Informationsstand des Betrachters abhängen. Der Betrachter ordnet aufgrund seines Kenntnisstandes den Ereignissen oder allgemein den in Frage kommenden Fällen "seine" Wahrscheinlichkeiten zu. Nach dieser subjektivistischen Wahrscheinlichkeitsauffassung können prinzipiell jeder Größe Wahrscheinlichkeiten zukommen. I. Ggs. zum Objektivisten ordnet ein Subjektivist auch den möglichen Werten des unbekannten Parameters Wahrscheinlichkeiten zu: Er stellt seinen Wissensstand über den Parameter als eine Verteilung auf dem Parameterraum dar. Formal läßt sich damit q als Realisation einer Zufallsgröße Z ("Zustand des Systems") auffassen. Entsprechend ist die Stichprobenverteilung als bedingte Verteilung von X1, ..., Xn unter der Bedingung Z = q anzusehen:
(5)     f(x1, ..., xn; q) = f(x1, ..., xn|q) Vor der Beobachtung der Stichprobe entspricht die Verteilung von Z den Vorkenntnissen des Betrachters über den Parameter. Die Wahrscheinlichkeitsfunktion bzw. Dichte dieser a priori Verteilung bezeichnen wir mit p(q) Nach der Beobachtung stellt die Verteilung von Z den neuen, aus Vorkenntnissen und Beobachtung resultierenden Informationsstand des Betrachters dar. Diese a posteriori Verteilung ist die bedingte Verteilung von Z unter der Bedingung: X1 = x1, ..., Xn = xn. Ihre Wahrscheinlichkeitsfunktion bzw. Dichte bezeichnen wir mit p(q|x1,..., xn) ; dafür gilt nach der Formel von Bayes:
(5)     p(q|x1,..., xn)  = cf (x1, ..., xn|q) * p(q) wobei c = c(x1, ..., xn) als Normierungsfaktor bestimmt wird. Das Grundkonzept der Bayes-Inferenz besteht in einem Lernvorgang: Aus der Beobachtung der Stichprobe wird dazugelernt, indem man mittels der Bayesschen Formel von der a priori auf die a posteriori Verteilung übergeht. Dieser Lernvorgang ist prinzipiell nicht wiederholbar, die Bayes-Inferenz mithin nichtfrequentistisch: Nach der Beobachtung spielt nur die eine vorliegende Stichprobe eine Rolle. Oft ist es zweckmäßig, sich nicht mit der Angabe der a posteriori Verteilung zu begnügen, sondern noch weitere Schlüsse aus der Stichprobe zu ziehen, die zu schärferen Aussagen über q führen. Diese Schlüsse müssen auf die a posteriori Verteilung aufbauen. Innerhalb der hier dargestellten nicht entscheidungstheoretisch orientierten Bayes-Inferenz dient dazu als Punktschätzung der Modalwert der a posteriori Verteilung und als Intervallschätzung ein "Bayes-Intervall", das ist ein möglichst kurzes Intervall, in dem q mit einer a posteriori Wahrscheinlichkeit von mindestens g liegt (g vorgegeben). Statistische Entscheidungstheorie. Die drei bisher besprochenen Konzepte der I. haben eines gemeinsam: Die Auswertung der Stichprobe soll Kenntnisse über den unbekannten Parameter vermitteln, der Schluß aus der Stichprobe stellt eine Aussage über den Parameter dar (statistical inference). Demgegenüber wird innerhalb des vierten Konzeptes, der statistischen Entscheidungstheorie, die Auswertung einer Stichprobe als Bestandteil eines Entscheidungsproblems aufgefaßt, die Auswertung (statistical decision) soll eine Entscheidung zwischen verschiedenen Handlungsalternativen herbeiführen. Der Betrachter (Entscheidungsträger) verfügt über eine Menge von Aktionen a, deren Nutzen oder Schaden durch den unbekannten Parameter q beeinflußt wird. Die entsprechende Verlustfunktion L muß bekannt sein: L(q, a) stellt den Verlust dar, der entsteht, wenn bei Vorliegen des Parameterwertes q die Aktion a durchgeführt wird (negativer Verlust = Gewinn). Die Entscheidung, welche Aktion ergriffen werden soll, wird von der Beobachtung einer Stichprobe abhängig gemacht. Formal bedient man sich dazu einer Entscheidungsfunktion (Strategie) d, die jeder möglichen Stichprobe  x1, ..., xn eine Aktion a = d(x1, ..., xn) zuordnet. Bei Anwendung der Strategie d entsteht nach der Beobachtung x1, ..., xn der von q abhängige Verlust L(q, d(x1, ..., xn)), eine Realisation der Zufallsgröße L(q; d(X1, ..., Xn)). Deren Erwartungswert - gebildet mit der Stichprobenverteilung f(x1, ..., xn; q)  gibt in Abhängigkeit von q an, welchen Verlust man bei Benutzung der Strategie d vor der Beobachtung der Stichprobe zu erwarten hat. Diesen von


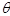
 abhängigen Erwartungswert nennt man die Risikofunktion Rd(q) der Strategie d. Eine Strategie ist umso besser, desto kleiner ihre Risikofunktion ist; genauer: Eine Strategie d ist (gleichmäßig) besser als eine Strategie e, wenn gilt: Rd(q) £ Re(q) für alle q und Rd(q) < Re(q) für mindestens ein q. Allerdings ist damit noch nicht gewährleistet, daß auch stets zwei Strategien miteinander vergleichbar sind. Vielmehr tritt oft der Fall ein, daß sich die Risikofunktionen zweier Strategien schneiden, die beiden Strategien mithin unvergleichbar sind. Nicht nur die durchgängige Vergleichbarkeit von Strategien, sondern auch die Definition einer optimalen Strategie innerhalb der Menge aller Strategien scheitert i.d.R. an der Abhängigkeit der Risikofunktion von q. Um dennoch mit Hilfe der Risikofunktion zu erklären, was man unter einer besten Strategie versteht, muß man entweder die Menge aller Strategien auf eine Teilklasse von Strategien mit gewissen wünschenswerten Eigenschaften einschränken oder zusätzliche, auf die Risikofunktion aufbauende Kriterien heranziehen, die die Abhängigkeit von q überwinden. Das bekannteste darunter ist das Minimax-Kriterium, nach dem eine Strategie optimal ist, wenn für sie das Maximum der Risikofunktion minimal ist. Solche Minimax-Strategien werden von extrem vorsichtigen (pessimistischen) Entscheidungsträgern bevorzugt, die mit dem ungünstigsten q-Wert rechnen. Besonders elegant wird die statistische Entscheidungstheorie, wenn auch noch (subjektives) Vorwissen über q in Form einer a priori Verteilung p(q) berücksichtigt wird. Damit läßt sich nämlich das (a priori) zu erwartende oder mittlere Risiko            


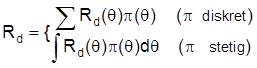
        einer Strategie d bilden. Man nennt Rd das (a priori) Bayes-Risiko von d. Da Rd nicht mehr von q abhängt, lassen sich vermöge des Bayes-Risikos alle Strategien miteinander vergleichen. Konsequenterweise gilt die Strategie als optimal  man nennt sie Bayes-Strategie , deren Bayes-Risiko am kleinsten ist. Die statistische Entscheidungstheorie kann als ein formaler Überbau der verschiedenen Konzepte der I. angesehen werden: Schätzprobleme (Punkt- und Intervallschätzungen) und Testprobleme lassen sich auch als Entscheidungsprobleme (mit oder ohne a priori Verteilungen) formulieren, die Entscheidungstheorie ist offen für den objektivistischen und subjektivistischen Standpunkt. Vor allem die Bayes-Inferenz tendiert stark zu einer entscheidungstheoretischen Darstellung, zumal manche Schlußweisen (z.B. Tests und bestimmte Punktschätzverfahren) nur dann in das Repertoire eines Bayesianers passen, wenn sie entscheidungstheoretisch aufgefaßt werden. Durch den entscheidungstheoretischen Ansatz wird ein Schluß von einer Stichprobe auf eine Grundgesamtheit allerdings nur dann inhaltlich adäquat erfaßt, wenn sich der Betrachter in einer realen Entscheidungssituation befindet und die zugrundegelegte Verlustfunktion sachlich begründen kann. In allen anderen Fällen ist eher eines der drei erstgenannten nichtentscheidungstheoretischen Inferenz-Konzepte angezeigt. Eine konkrete Entscheidungssituaiton ist insbesondere dann schwer zu begründen, wenn die Stichprobe wissenschaftlichen Untersuchungen dient, die zu Erkenntnissen innerhalb der betreffenden Wissenschaft führen sollen.

Literatur: V. Barnett, Comparative statistical inference.
2. A., Chichester  New York  Brisbane  Toronto  Singapore 1982. D. R. Cox/D. V. Hinkley, Theoretical statistics. London 1974. M. G. Kendall/A. Stuart, The advanced theory of statistics. Vo. 1: Distribution theory.
5. A., London 1977. M. G. Kendall/A. Stuart, The advanced theory of statistics. Vol. 2: Inference and Relationship.
5. A., London 1979. M. G. Kendall/A. Stuart/J. K. Ord, The advanced theory of statistics. Vol. 3: Design and analysis, and timeseries.
5. A., London 1983. J. Pfanzagl, Allgemeine Methodenlehre der Statistik. Band II.
5. A., Berlin  New York 1978. B. Rüger, Induktive Statistik.
2. A., München  Wien 1988.