|
Zinsoptionen, Bewertung von
Inhaltsübersicht
I. Zinsoptionen
II. Grundsätzliche Probleme bei der Bewertung von Optionen auf Zinsinstrumente und Modellübersicht
III. Kursmodelle
IV. Klassische Faktormodelle
V. Kassa- und Terminzinssatzmodelle bei vollständiger Information
VI. Empirische Ergebnisse
I. Zinsoptionen
Die von der Bank für Internationalen Zahlungsausgleich durchgeführten Markterhebungen zeigen, dass etwa zwei Drittel des Volumens an Derivaten auf Zinsderivate entfallen. 80% der ausstehenden Zinsderivate werden over-the-counter (OTC), 20% an Terminbörsen gehandelt. Die OTC-Kontrakte setzen sich aus Swaps, Forward-Rate-Agreements und Optionen auf Kassa- sowie Termininstrumente, die börsengehandelten Zinsderivate aus Zinsfutures sowie aus Optionen auf Futures und auf Kassazinssätze zusammen. OTC-Zinsoptionen entstehen durch eine direkte Vereinbarung zwischen Käufer und Verkäufer des Kontraktes. Als Basisinstrument werden in der Regel ein Zinssatz, eine Anleihe oder ein OTC-Terminkontrakt vereinbart. Die beiden wichtigsten Gruppen von OTC-Zinsoptionen bilden Caps bzw. Floors und Swaptions. Ein Cap besteht aus einem Portefeuille von Caplets. Jedes Caplet kann als ein Call auf den in einem zukünftigen Zeitpunkt t festgestellten Zinssatz, meist ein Geldmarktzinssatz, aufgefasst werden. Übersteigt der Referenzzinssatz r an diesem Termin das vereinbarte maximale Zinsniveau k (Basispreis), erhält der Käufer des Caps am Ende der Zinsperiode eine zu dieser Zinsdifferenz r – k proportionale Ausgleichszahlung. Bei einer Swaption besitzt der Inhaber das Recht, in einem zukünftigen Zeitpunkt als Fixed-Payer oder Fixed-Receiver in einen Zinsswap mit vorgegebenem Swapsatz k und fester Fälligkeit einzutreten. Im ersten Fall liegt eine Payer-, im zweiten eine Receiver-Swaption vor. Diese Option wird vom Inhaber ausgeübt, wenn im Entscheidungspunkt der relevante Swapsatz über bzw. unter k liegt. Ihr Ausübungswert ergibt sich dann als die Summe der diskontierten Zinsersparnisse bzw. Zinsmehreinnahmen. Für Caps und Swaptions existiert in allen wichtigen Währungen ein liquider und standardisierter Markt. Daneben gibt es weitere, aber weniger liquide Märkte für exotische Zinsoptionen, für Swaps mit Optionskomponenten sowie für Anleihen, bei denen einzelne Ausstattungsmerkmale mit Optionen für die Emittentin oder den Inhaber ausgestattet sind (Mayer, 1998; Bardenhewer, M. 2000; Mason, R. 1986).
Die Mehrzahl der börsengehandelten Optionen beziehen sich auf ebenfalls börsengehandelte Financial Futures, denen ihrerseits meist Emissionen staatlicher Emittenten zugrunde liegen. Die Ausübung dieser Optionen kann in der Regel jederzeit erfolgen (amerikanischer Typ). Bei den an der CBoT gehandelten Optionen auf Zinsfutures muss der Optionskäufer die Optionsprämie bei Abschluss bezahlen. Dagegen werden die Zinsoptionen der EUREX und LIFFE wie Futures über ein tägliches Markt-to-Market abgerechnet (Future-Style Optionen). Neben Optionen auf Zinsfutures existieren auch einige Kontrakte auf Kassatitel. Ein Beispiel hierfür bilden die an der CBOE gehandelten Optionen auf Renditen von Treasury Bills, Treasury Notes und Treasury Bonds.
II. Grundsätzliche Probleme bei der Bewertung von Optionen auf Zinsinstrumente und Modellübersicht
Die Bewertung von Zinsoptionen und Optionen auf andere Basisinstrumente wie Aktien oder Devisen unterscheidet sich in einigen wesentlichen Punkten. Dies gilt unabhängig davon, ob ein zins- oder kursbasiertes Modell gewählt wird (vgl. Abb. 1). Die wichtigsten Unterschiede betreffen die folgenden Punkte:
| - | Bei Anleihen mit endlicher Laufzeit ist der Anleihekurs bei nichtnegativen nominalen Zinssätzen nach oben beschränkt und muss bei einem Ausschluss von Ausfallrisiken gegen den Rückzahlungskurs konvergieren. | | - | Die Kurs- und Renditevolatilität einer Anleihe verändert sich mit Abnahme der Restlaufzeit. | | - | Neben dem Kurs- oder Zinsverlauf des Basisinstruments muss mindestens ein weiteres Zinsinstrument modelliert werden. Bei amerikanischen Optionen oder bei der simultanen Bewertung verschiedener Zinsderivate ist sogar die Dynamik eines multidimensionalen Zins- oder Kursprozesses arbitragefrei zu beschreiben. |
Die zuletzt herausgearbeitete Problematik einer arbitragefreien Modellierung der Zinsstrukturkurve bildet den Kern der Bewertung von Zinsoptionen. Die eigentliche Bewertung stellt demgegenüber ein nachgeordnetes Problem dar. Die nachstehende Klassifikation der Bewertungsmodelle für Zinsoptionen orientiert sich deshalb auch daran, ob und inwieweit Informationen über die aktuelle Zinsstrukturkurve und deren Dynamik eingehen. So werden bei den Kursmodellen nur die Kurse des Basisinstruments und eines alternativen Zinstitels erfasst, während in den klassischen Faktormodellen die gesamten modellendogen ermittelten Zinsstrukturkurven berücksichtigt werden. Im zweiten Schritt erfolgt dann die Bewertung der Zinsoption relativ zu diesen endogenen Zinsstrukturkurven. Die Modelle mit vollständiger Information verwenden zusätzlich die exogen verfügbare aktuelle Kassa- bzw. Terminzinssatzkurve und möglicherweise auch die aktuelle Volatilitätsstrukturkurve der Zinssätze.
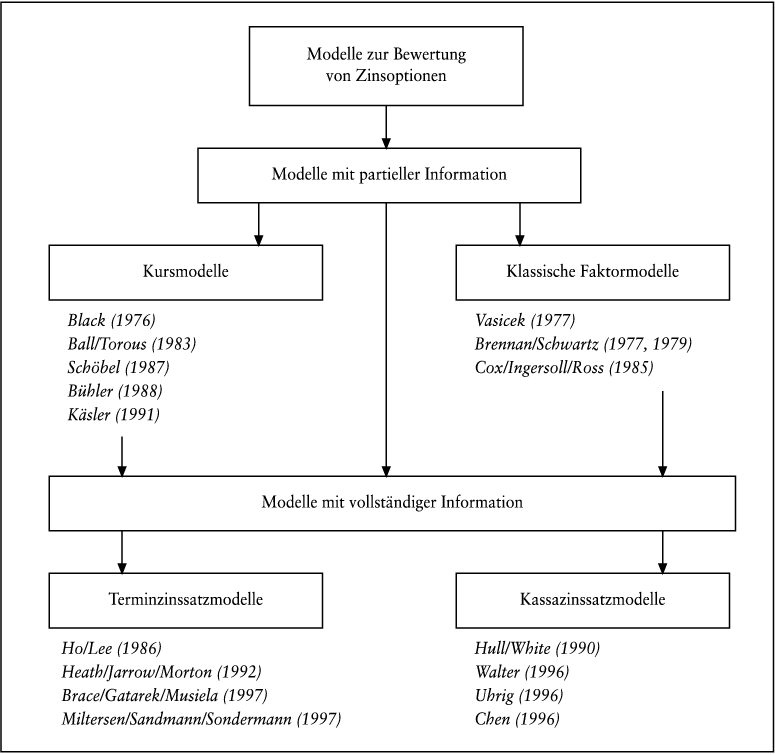
Abb. 1: Modelle zur Bewertung von Zinsoptionen
III. Kursmodelle
Ausgangspunkt aller Kursmodelle ist eine Beschreibung des zufälligen Kursverlaufs des Basistitels. In einer ersten Gruppe von Modellen wird der Kurs als Brown\'scher Brückenprozess formuliert. Dieser auf Ball und Torous zurückgehende Ansatz stellt sicher, dass der Kurs der Anleihe bei Fälligkeit mit ihrem Rückzahlungskurs übereinstimmt (Ball, C./Torous, W. 1983). Da diese Eigenschaft jedoch bei konstanter Volatilität σ ausschließlich über eine geeignete Spezifizierung der Drift erreicht wird, diese jedoch für den arbitragefreien Wert einer Option keine Bedeutung besitzt, kann dieses Modell die Eigenschaften von langlaufenden Zinsoptionen nicht korrekt abbilden.
Das Modell von Ball/Torous zeigt zugleich die Grenzen der lokalen Charakterisierung von Optionswerten mit Hilfe von partiellen Differentialgleichungen auf. So weist Cheng nach, dass zu den als Brown\'sche Brückenprozesse modellierten Anleihekursen kein äquivalentes Martingalmaß existiert und damit die Arbitragefreiheit dieser Modelle offen ist (Cheng, S. 1991). Diese Problematik wird durch Bühler und Käsler gelöst (Bühler, W./Käsler, J. 1989; Käsler, J. 1991), indem sie den Kursprozess des Basisinstruments relativ zum Kursprozess desjenigen Zero Bonds modellieren, dessen Restlaufzeit mit der Optionsfrist übereinstimmt. Dieses Modell ist arbitragefrei, führt mit Wahrscheinlichkeit eins zu positiven Zinssätzen und erlaubt eine analytische Lösung für Optionen auf Zero Bonds.
Eine zweite Gruppe von Modellen basiert auf dem Modell von Black, bei dem die speziellen Eigenschaften von Anleihekursen jedoch nicht berücksichtigt werden (Black, F. 1976). Als Basisinstrument wird hierbei ein Future auf eine Anleihe oder einen Geldmarkttitel betrachtet. Für die Bewertung einer europäischen Option auf ein Kassainstrument müssen dann die Fälligkeit des Futures und der Verfallstermin der Option zusammenfallen, da in diesem Zeitpunkt der Futurekurs mit dem Kurs des Kassainstruments übereinstimmt.
Der Wert einer Europäischen Option auf einen Future lässt sich unmittelbar aus der Black/Scholes\'schen Replikationsstrategie zusammen mit der Überlegung ableiten, dass mit dem Kauf eines Futures kein Kapitaleinsatz verbunden ist. Für einen Call mit Fälligkeit im Zeitpunkt T und Basispreis E auf einen Future mit dem aktuellen Kurs F0 ergibt sich dann
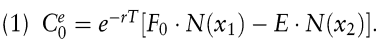
Hierbei bezeichnet wie in der Black/Scholes-Formel N (x1) das Call-Delta und N (x2) die Wahrscheinlichkeit der Optionsausübung bzgl. der risikoneutralen Wahrscheinlichkeitsverteilung des Futurekurses.
Die Black-Formel stellt den Marktstandard bei der Bewertung von Caps und Swaptions dar. Dabei werden im Falle eines Caps so viele lognormal verteilte Terminzinssätze fi (t) (i = 1, ..., n) wie Caplets bzw. Zinsanpassungstermine modelliert. Der Terminzinssatz fi stimmt bei Fälligkeit mit dem Kassazinssatz für die Zinsanpassungsfrist Δti überein. Zur Ermittlung des Wertes des i-ten Caplets im Zeitpunkt t = 0 wird dann in der Bewertungsbeziehung (1) der Futurepreis Ft durch fi(0), E durch die Zinsgrenze k und der Diskontierungsfaktor durch den Preis des in ti+1 fälligen Zero Bonds ersetzt.
Diese Vorgehensweise der Praxis wurde lange kritisiert, da lognormal verteilte Momentanzinssätze Arbitragemöglichkeiten eröffnen (Heath, D./Jarrow, R./Morton, A. 1992; Hogan, M./Weintraub, K. 1993). Brace, / et al. und Miltersen, et al. haben jedoch gezeigt, dass bei vorgegebenen Zinsperioden Δ ti die Black-Formel aus dem arbitragefreien Heath/Jarrow/Morton-Modell abgeleitet werden kann (Brace, A./Gatarek, D./Musiela, M. 1997; Miltersen, K./Sandmann, K./Sondermann, D. 1997; Heath, D./Jarrow, R./Morton, A. 1992). Damit ist die Anwendung der Black-Formel für die Bewertung von Caps auch aus theoretischer Sicht gerechtfertigt.
IV. Klassische Faktormodelle
Bei der Bewertung von Zinsoptionen reicht in der Regel die Modellierung der Kurse einiger weniger Anleihen nicht aus. So ist bei der simultanen Bewertung eines gesamten Handelsbestandes an Zinsderivaten oder bei der Bewertung einer amerikanischen Zinsoption die Dynamik der Zinssätze für eine Vielzahl von Fälligkeiten erforderlich. Hierbei stellen sich zwei Kernprobleme. Erstens ist sicherzustellen, dass die theoretisch unendlich vielen Zinssätze im Zeitablauf in dem Sinne konsistent modelliert werden, dass keine Arbitragemöglichkeiten entstehen. Zweitens sollte die gesamte Zinsstrukturkurvenbewegung durch wenige Faktoren beschrieben werden, damit die theoretischen Bewertungs- und die praktischen Anwendungsprobleme beherrschbar bleiben. Abb. 2 gibt einen Überblick über die Struktur der entwickelten Faktormodelle.
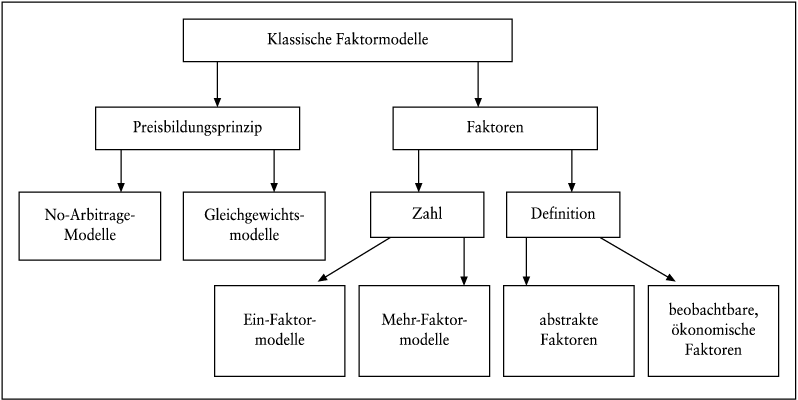
Abb. 2: Typologie klassischer Faktormodelle
1. Ein-Faktormodelle
Die Struktur der Ein-Faktormodelle wird zunächst unter Verwendung des No-Arbitrage-Ansatzes dargestellt. Ausgangspunkt ist die exogen vorgegebene stochastische Entwicklung des Momentanzinssatzes rt in der Form
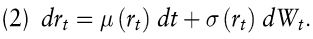
Beide Größen, die Drift μ(rt) und die Volatilität σ(rt) des Momentanzinssatzes, besitzen die Dimension [% p.a.].
Hängt der Wert eines beliebigen Zinsinstruments, z.B. eines Zero Bonds oder einer Zinsoption, nur von dessen Ausstattungsmerkmalen, dem aktuellen Momentanzinssatz und dem aktuellen Zeitpunkt ab, dann lässt zeigen, dass in einem No-Arbitrage-Gleichgewicht die relativen Überschussrenditen aller Zinsinstrumente übereinstimmen müssen, d.h. es muss
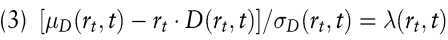
gelten. In (3) bezeichnet D (rt , t) den No-Arbitrage-Wert des betrachteten Zinsinstruments, μD(rt, t) dessen erwartete Wertänderung und σD(rt, t) die Standardabweichung der Wertänderung jeweils auf Jahresbasis. λD(rt, t) wird als Marktpreis des Zinsrisikos bezeichnet. Diese Größe hängt nur vom exogenen Momentanzinssatz und der Kalenderzeit, nicht aber von den Ausstattungsmerkmalen des Zinsinstruments ab.
Aussagen über Struktur und Höhe des Marktpreises des Risikos erfordern die Spezifizierung eines Gleichgewichtsmodells. Im Falle eines Produktions-Tauschgleichgewichts mit einer ungewissen Zustandsvariablen und einem repräsentativen Investor mit logarithmischer Nutzenfunktion ist der Marktpreis des Risikos proportional zu σ(rt) und die Bewertungsgleichung (3) erlaubt für einfache Zinsprozesse eine explizite Lösung (Cox, J./Ingersoll, J./Ross, E. 1985). Hierzu zählen insbesondere die affinen Ein-Faktormodelle. Sie sind charakterisiert durch folgende Drift- und Diffusionskoeffizienten für den Momentanzinssatz rt:
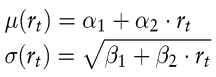
Für diese Modellklasse besitzen die Werte B(rt, t, T) von Zero Bonds die folgende Struktur:
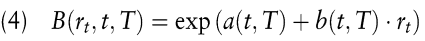
Hierbei sind a (t, T) und b (t, T) elementare Funktionen, die nur von der Restlaufzeit T – t des Zero Bonds und den Parametern des Zinsprozesses abhängen. Aus (4) lässt sich durch Logarithmierung unmittelbar die zugehörige arbitragefreie Dynamik der Zinsstrukturkurven gewinnen.
Das Vasicek-Modell und das Cox/Ingersoll/Ross-Modell bilden die beiden wichtigsten Zinsmodelle mit affiner Struktur (Vasicek, O. 1977; Cox, J./Ingersoll, J./Ross, E. 1985). Sie sind durch eine „ mean-reverting “ -Drift der Form
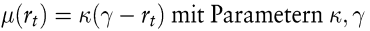
und die Diffusionskoeffizienten
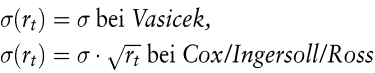
charakterisiert. Alle Kassazinssätze im Vasicek-Modell sind normalverteilt, im Cox/Ingersoll/Ross-Modell nichtzentral chi-quadratverteilt.
Für beide Modelle lassen sich auch explizite Formeln für Europäische Optionen auf Anleihen, Kassazinssätze und Futures ableiten. Dieses Ergebnis beruht auf den speziellen Verteilungseigenschaften der Momentanzinssätze und auf der einfachen Struktur der Marktpreise des Zinsrisikos: konstant im Vasicek-Modell und proportional zu 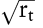 im Cox/Ingersoll/Ross-Modell. Dadurch besitzen die Momentanzinssätze bzgl. der risikoadjustierten Wahrscheinlichkeiten dieselben Verteilungseigenschaften wie vor Risikoadjustierung. Es ergibt sich dann für einen europäischen Call auf einen Zero Bond mit Laufzeit T^ im Cox/Ingersoll/Ross-Modell. Dadurch besitzen die Momentanzinssätze bzgl. der risikoadjustierten Wahrscheinlichkeiten dieselben Verteilungseigenschaften wie vor Risikoadjustierung. Es ergibt sich dann für einen europäischen Call auf einen Zero Bond mit Laufzeit T^
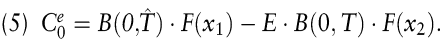
Die kumulative Verteilungsfunktion F in (5) ist im Vasicek-Modell durch die kumulative Normalverteilung N und im Cox/Ingersoll/Ross-Modell durch die Verteilungsfunktion einer nichtzentral chi-quadratverteilten Zufallsgröße definiert, deren Parameter durch den Zinsprozess und die Ausstattungsmerkmale der Option festgelegt sind.
2. Mehr-Faktormodelle
Offensichtlich können realistische Bewegungen der Zinsstrukturkurve mit Hilfe von Ein-Faktormodellen nicht angemessen repräsentiert werden, da lokale Änderungen von Zinssätzen unterschiedlicher Fristigkeit vollständig positiv korreliert sind. Es liegt deshalb nahe, die Dynamik der Zinsstrukturkurve durch mehr als einen Faktor zu charakterisieren.
In einer ersten Gruppe von Ansätzen werden Zinssätze als Faktoren gewählt (Brennan, M./Schwartz, E. 1979; Walter, U. 1996). Autoren einer zweiten Gruppe von Arbeiten erweitern Ein-Faktormodelle des Abschnitts 1, indem sie einen oder mehrere Parameter des Zinsprozesses für rt ebenfalls als stochastischen Prozess modellieren (Chen, L. 1996). In den Ansätzen der dritten und allgemeinsten Gruppe werden die Faktoren als abstrakte Größen modelliert. Als Beispiel können das allgemeine Gleichgewichtsmodell von Cox/Ingersoll/Ross und dessen spezielle Variante von Uhrig genannt werden (Cox, J./Ingersoll, J./Ross, E. 1985; Uhrig, M. 1996).
Auch bei den Mehr-Faktormodellen besitzen die Ansätze mit affinen unkorrelierten Faktoren eine besondere Bedeutung, da sie eine analytische Darstellung der Zinsstrukturkurve erlauben. Das folgende spezielle Zwei-Faktormodell illustriert diesen Sachverhalt (Walter, U. 1996): Der erste Faktor wird durch die Rendite lt eines lang laufenden Zerobonds repräsentiert. Die stochastische Entwicklung von lt genügt einem Wurzelprozess des Cox/Ingersoll/Ross-Typs. Als zweiter Faktor wird der Spread st := lt – rt gewählt, der als Ornstein/Uhlenbeck-Prozess wie im Vasicek-Modell modelliert wird. Der Wert eines Zero Bonds besitzt dann die folgende Struktur
(6) 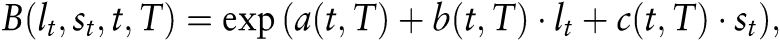
d.h. er lässt sich als Produkt zweier Komponenten darstellen, wobei jede die für ein affines Ein-Faktormodell abgeleitete Form (4) besitzt. Daraus folgt unmittelbar, dass die Zinsstrukturkurve y(T, lt, st) = – (a(t, T) + b(t, T) · lt + c (t, T) · st)/T linear von den beiden Faktoren lt und st abhängt. Auch für den Wert von europäischen Optionen auf Zero Bonds und damit für Caps lässt sich wieder eine analytische Darstellung der Form (5) angeben.
V. Kassa- und Terminzinssatzmodelle bei vollständiger Information
1. Kassazinssatzmodelle
Klassische Faktormodelle besitzen einen wesentlichen Nachteil: Die für den Bewertungszeitpunkt t = 0 ermittelte endogene Zinsstrukturkurve stimmt in aller Regel nicht mit der aktuellen, grundsätzlich beobachtbaren Zinsstrukturkurve überein. Dasselbe gilt für die Volatilitätsstrukturkurve, definiert als die Volatilität der Renditen von Zero Bonds in Abhängigkeit der Restlaufzeit.
Cox/Ingersoll/Ross schlagen vor, die Freiheitsgrade klassischer Faktormodelle dadurch zu erhöhen, dass die Drift des Momentanzinssatzes zusätzlich von der Kalenderzeit abhängt (Cox, J./Ingersoll, J./Ross, E. 1985, S. 395). Die Struktur der zeitabhängigen Drift soll dann im Rahmen eines „ Inversionsprozesses “ in der Weise festgelegt werden, dass die endogene Zinsstrukturkurve mit der am Markt beobachteten exogenen übereinstimmt.
Im Allgemeinen wird die Bestimmung der zeitabhängigen Drift nur auf numerischem Weg möglich sein. Vorschläge hierzu gehen auf Hull/White und Uhrig/Walter zurück (Hull, J./White, A. 1996; Uhrig, M./Walter, U. 1996). Im Falle des Vasicek-Modells kann das Inversionsproblem jedoch analytisch gelöst werden (Hull, J. 1990). Hierbei wird die Funktion a(t, T) in der Bewertungsgleichung (4), die ihre Struktur auch bei zeitabhängigem Parameter γ(t) behält, in der Weise festgelegt, dass die aus B(r0, 0, T) errechneten Modellrenditen mit der aktuellen Zinsstrukturkurve übereinstimmen. Diese Vorgehensweise lässt sich auch auf Mehr-Faktormodelle übertragen.
Eine zusätzliche Anpassung eines Modells an die aktuelle Volatilitätsstrukturkurve kann grundsätzlich über die zeitabhängige Formulierung eines zweiten Parameters, z.B. der Volatilität σ oder des Mean-Reversion-Parameters κ, erfolgen. Die Kalibrierung lässt sich dann unter Verwendung von Preisen für Caps oder Swaptions vornehmen. Es zeigt sich aber, dass diese Vorgehensweise für Ein-Faktormodelle zu unplausiblen zukünftigen Volatilitätsstrukturen führt (Walter, U. 1996). Aus diesem Grund sollten bei der simultanen Kalibrierung eines Modells zur Bewertung von Zinsoptionen an die Zins- und Volatilitätsstrukturkurve mindestens zwei Faktoren berücksichtigt werden. Rebonato berichtet ausführlich über Erfahrungen bei der Anpassung unterschiedlicher Kassazinsmodelle an Zins- und Volatilitätsdaten (Rebonato, R. 1998).
Wenn die Kalibrierung eines Faktormodells an die aktuelle Zins- und Volatilitätsstrukturkurve nur numerisch möglich ist, können auch die Werte von Optionen auf Zinsintrumente nur noch numerisch ermittelt werden. Im Falle des Vasicek-Modells mit seinem normalverteilten Zinsfaktor lassen sich jedoch bei einem zur Kalibrierung verwendeten zeitabhängigen Faktor γ (t) Optionswerte analytisch ermitteln. Es ergibt sich für den Wert eines Calls wiederum eine Bewertungsformel des Black/Scholes-Typs (5). Dieses Ergebnis lässt sich auch auf Modelle mit mehreren normalverteilten Faktoren erweitern.
2. Terminzinssatzmodelle
Die Kalibrierung eines Kassazinssatzmodells an die aktuelle Marktinformation kann ein sehr aufwendiger Prozess sein. Eine Alternative stellt die auf Ho/Lee und Heath/Jarrow/Morton zurückgehende Vorgehensweise dar (Ho, T./Lee, S. 1986; Heath, D./Jarrow, R./Morton, A. 1992). Bei diesen Modellen wird eine aktuelle Zins- und Volatilitätsstrukturkurve vorgegeben und die Dynamik der Zinsstrukturkurve bedingt zu dieser Information in arbitragefreier Weise modelliert. Da die aktuelle Zinsinformation meist durch Terminzinssätze dargestellt wird, hat sich für diese Modellklasse auch die Bezeichnung Terminzinssatzmodelle eingebürgert.
Im Weiteren werden zeitstetige Terminzinssatzmodelle mit einem (abstrakten) Faktor auf der Basis von Momentan-Terminzinssätzen f (t, T) betrachtet. Hierbei bezeichnet t die Kalenderzeit und T den Beginn der „ kurzen “ , bis T + dt reichenden Zinsperiode für das Termingeschäft. Eine Verallgemeinerung auf mehr als einen Faktor ist unmittelbar möglich (vgl. Heath, D./Jarrow, R./Morton, A. 1992). In Analogie zum Momentanzinssatz wird die stochastische Entwicklung des Terminzinssatzes in der folgenden Weise charakterisiert:
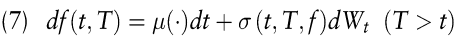
Das zentrale Ergebnis von Heath/Jarrow/Morton besagt, dass die nicht genauer spezifizierte Drift (bzgl. der risikoneutralen Wahrscheinlichkeiten) bereits durch die Diffusionskoeffizienten vollständig festgelegt ist:
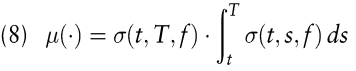
Die einfachsten Varianten des Heath/Jarrow/Morton-Modells ergeben sich, wenn die Diffusionskoeffizienten nicht vom Terminzinssatz abhängen. In diesem Fall sind die Terminzinssätze normalverteilt. Optionen auf Zero Bonds lassen sich dann wieder analytisch bewerten und die Bewertungsformel besitzt die in (5) dargestellte Struktur.
Bei allen Kassa- und Terminzinssatzmodellen mit normalverteilten Faktoren wird der Vorteil, dass sich eine große Zahl von Zinsoptionen analytisch bewerten lassen, durch den offensichtlichen Nachteil erkauft, dass Kassa- und Terminzinssätze negative Werte annehmen können. Zur Vermeidung dieses Nachteils liegt es nahe, normalverteilte Faktoren durch logarithmisch normalverteilte zu ersetzen. Heath/Jarrow/Morton haben jedoch darauf hingewiesen, dass die auf den ersten Blick unproblematische Dynamik
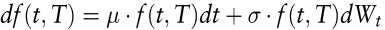
von Terminzinssätzen zu Arbitragemöglichkeiten führt. Ein analoges Ergebnis wurde von Hogan/Weintraub für logarithmisch normalverteilte Momentanzinssätze rt bewiesen (Hogan, M./Weintraub, K. 1993).
Beide Resultate waren der Anlass, statt des theoretischen Konstrukts „ Momentanzinssätze “ Marktkonventionen bei der Definition von Zinssätzen zu verwenden. So konnten Miltersen/Sandmann/Sondermann zeigen, dass arbitragefreie Modelle für die Zinsstrukturkurve auf der Basis von logarithmisch normalverteilten Terminzinssätzen entwickelt werden können, wenn sich diese auf eine Zinsperiode positiver Länge, z.B. drei Monate, beziehen (Miltersen, K./Sandmann, K./Sondermann, D. 1997). Diese Modelle erlauben es ebenfalls, Europäische Optionen auf Zero Bonds analytisch zu bewerten. Die Bewertungsformel besitzt allerdings eine allgemeinere Struktur als die Black/Scholes-Formel und stimmt mit dem von Bühler/Käsler abgeleiteten Ergebnis überein (Bühler, W./Käsler, J. 1989). Ein Nachteil dieser Modelle mit positiver Zinsperiode besteht darin, dass Zinsoptionen, die auf Zinssätzen anderer Fristigkeit basieren, nicht analytisch bewertet werden können, da bei linearer Zinsrechnung aufeinanderfolgende dreimonatige Zinssätze und der zugehörige sechsmonatige Zinssatz nicht alle logarithmisch normalverteilt sein können.
3. Zusammenhänge zwischen Kassa- und Terminzinssatzmodellen
Zu jedem Terminzinssatzmodell existiert aufgrund der definitorischen Beziehung rt = f (t, t) ein äquivalentes Kassazinssatzmodell. Allerdings wird, außer in Sonderfällen, die Änderung drt des Momentanzinssatzes nicht nur von den aktuellen Werten der Faktoren abhängen (Markov-Eigenschaft), sondern von deren gesamten Historie. Für Ein-Faktormodelle hat Jeffrey gezeigt, dass in die Volatilitäten aller Terminzinssätze außer den beiden Zeitvariablen t und T nur noch der aktuelle Momentanzinssatz rt bzw. f (t, t) eingehen darf, damit das Kassazinssatzmodell die Markov-Eigenschaft besitzt. Dies ist also insbesondere dann erfüllt, wenn σ(t, T, f) nicht von f abhängt (Jeffrey, A. 1995).
Umgekehrt existiert auch zu jedem Kassazinssatzmodell ein äquivalentes Terminzinssatzmodell. Die stochastische Entwicklung der Terminzinssätze kann dabei grundsätzlich aus der Dynamik der Zero-Bondpreise abgeleitet werden, indem die Beziehung
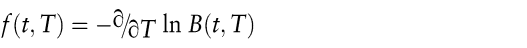
zwischen Momentan-Terminzinssätzen und den aus dem Kassazinssatzmodell gewonnenen Zero-Bondpreisen ausgenutzt wird.
Besonders einfach gestalten sich die Zusammenhänge zwischen Kassa- und Terminzinssatzmodellen, wenn die Faktoren normalverteilt sind. So stimmen die Volatilitäten des Kassazinssatzes rt und der Terminzinssätze im zeitstetigen Ho/Lee-Modell überein. Im Ein-Faktor-Vasicek-Modell gehört zu der Volatilität σ des Momentanzinssatzes rt die exponentiell in T abnehmende Volatilität
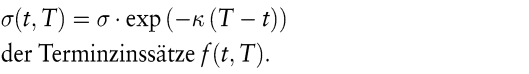
VI. Empirische Ergebnisse
Die beiden umfangreichsten empirischen Studien gehen auf Amin/Morton und Bühler et al. zurück (Amin, K./Morton, A. 1994; Bühler, W. et al. et al. 1999). Amin/Morton testen sieben Ein-Faktor-Terminzinssatzmodelle im Markt der Optionen auf Eurodollar-Futures. Bei der Erklärung beobachteter Optionspreise erzielen die beiden Modelle mit den Volatilitätsfunktionen
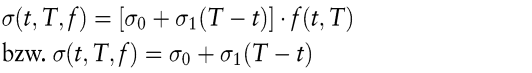
die niedrigsten prozentualen absoluten Fehler.
Bühler et al. testen sieben Kassa- und Terminzinssatzmodelle im Markt der Zinsoptionsscheine auf Bundesanleihen (Bühler, W. et al. et al. 1999). Die Gruppe der Kassazinssatzmodelle umfasst ein Ein-Faktormodell sowie zwei Zwei-Faktormodelle. Bei diesem werden der langfristige Zinssatz und der Spread bzw. der Momentanzinssatz und dessen Volatilität als Faktoren verwendet. Die Gruppe der Terminzinssatzmodelle besteht aus zwei Ein- und zwei Zwei-Faktormodellen. Von den untersuchten Modellen erweist sich das Ein-Faktor-Kassazinssatzmodell als Ausreißer mit nicht akzeptablen Resultaten. Hinsichtlich der absoluten Abweichungen zwischen Modell- und Marktpreisen schneiden überraschenderweise die beiden Zwei-Faktor-Terminzinssatzmodelle am schlechtesten ab. Ihre mittleren absoluten Fehler liegen signifikant über denjenigen der anderen vier Modelle. Insgesamt verbleiben zwei Modelle, deren absoluter Bewertungsfehler bei Variation des Untersuchungsdesigns nie schlechter ausfällt als bei einem der anderen vier Modelle: das Ein-Faktor-Terminzinssatzmodell mit einer zu f(t, T) proportionalen Volatilität der Terminzinssätze und das Zwei-Faktormodell mit dem kurzfristigen Zinssatz und dessen Volatilität als Faktoren. Wird zusätzlich zur Bewertungsqualität der Aufwand zur Schätzung der Daten und zur numerischen Berechnung der Optionswerte berücksichtigt, sollte auf Basis der Ergebnisse dieser Studie dem einfaktoriellen Terminzinssatzmodell der Vorzug gegeben werden.
Literatur:
Amin, K./Morton, A. : Implied Volatility Functions in Arbitrage-Free Term Structure Models, in: JFE 1994, S. 141 – 180
Ball, C./Torous, W. : Bond Price Dynamics and Options, in: JFin.Quant 1983, S. 517 – 531
Bardenhewer, M. : Exotische Zinsswaps, Wiesbaden 2000
Black, F. : The Pricing of Commodity Contracts, in: JFE 1976, S. 167 – 179
Black, F./Scholes, M. : The Pricing of Options and Corporate Liabilities, in: JPol.E 1973, S. 637 – 654
Brace, A./Gatarek, D./Musiela, M. : The Market Model of Interest Rate Dynamics, in: Mathematical Finance 1997, S. 127 – 154
Brennan, M./Schwartz, E. : Savings Bonds, Retractable Bonds and Callable Bonds, in: JFE 1977, S. 67 – 88
Brennan, M./Schwartz, E. : Savings Bonds: Theory and Empirical Evidence, Monograph Series in Finance and Economics, H. 4/1979, New York University
Bühler, W. : Rationale Bewertung von Optionsrechten auf Anleihen, in: ZfbF 1988, S. 851 – 884
Bühler, W./Käsler, J. : Konsistente Anleihepreise und Optionen auf Anleihen, Working Paper, Universität Dortmund 1989
Bühler, W. et al. : An Empirical Comparison of Forward-Rate and Spot-Rate Models for Valuing Interest-Rate Options, in: JF 1999, S. 269 – 317
Chen, L. : Interest Rate Dynamics, Derivatives Pricing, and Risk Management, Berlin et al. 1996
Cheng, S. : On the Flexibility of Arbitrage-Based Option Pricing when Stochastic Bond Price Processes are Involved, in: JETheory 1991, S. 185 – 193
Cox, J./Ingersoll, J./Ross, E. : A Theory of the Term Structure of Interest Rates, in: ENM 1985, S. 385 – 408
Heath, D./Jarrow, R./Morton, A. : Bond Pricing and the Term Structure of Interest Rates: A New Methodology for Contingent Claim Valuation, in: ENM 1992, S. 77 – 105
Ho, T./Lee, S. : Term Structure Movements and Pricing Interest Rate Contingent Volatilities, in: JF 1986, S. 1011 – 1029
Hogan, M./Weintraub, K. : The Lognormal Interest Rate Model and Eurodollar Futures, Working Paper, Citibank New York 1993
Hull, J. : Pricing Interest-Rate Derivative Securities, in: RoFS 1990, S. 573 – 592
Hull, J./White, A. : Using Hull-White Interest Rate Trees, in: Journal of Derivatives, Spring 1996, S. 26 – 36
Jeffrey, A. : Single Factor Heath-Jarrow-Morton Term Structure Models Based on Markov Spot Interest Rate Dynamics, in: JFin.Quant 1995, S. 619 – 642
Käsler, J. : Optionen auf Anleihen, Diss. Dortmund 1991
Mason, R. : Innovations in the Structure of International Securities, Credit Suisse First Boston, Research Group 1986
Mayer, S. : Bewertung Exotischer Zinsderivate, Diss. Ulm 1998
Miltersen, K./Sandmann, K./Sondermann, D. : Closed Form Solutions for Term Structure Derivatives with Log-Normal Interest Rates, in: JF 1997, S. 409 – 430
Musiela, M./Rutkowski, M. : Martingale Methods in Financial Modelling, New York 1997
Rebonato, R. : Interest-Rate Option Models, 2. A., Chichester 1998
Sandmann, K. : Einführung in die Stochastik der Finanzmärkte, Berlin et al. 1999
Schöbel, R. : Zur Theorie der Rentenoption, Berlin 1987
Uhrig, M. : Bewertung von Zinsoptionen bei stochastischer Zinsvolatilität, Wiesbaden 1996
Uhrig, M./Walter, U. : A New Numerical Approach for Fitting the Initial Yield Curve, in: Journal of Fixed Income 1996, S. 82 – 90
Vasicek, O. : An Equilibrium Characterization of the Term Structure, in: JFE 1977, S. 177 – 188
Walter, U. : Die Bewertung von Zinsoptionen, Wiesbaden 1996
|