|
Investitionsrechnungen bei Unsicherheit
Inhaltsübersicht
I. Sichere und unsichere Investitionsentscheidungen
II. Investitionsplanung in offenen Entscheidungsfeldern
III. Planungsmethoden in geschlossenen Entscheidungsfeldern
IV. Kapitalmarktorientierte Bewertung unsicherer Investitionen
I. Sichere und unsichere Investitionsentscheidungen
1. Merkmale unsicherer Entscheidungen
Bei sicheren Informationen kann jeder Investition ein eindeutiger Zielwert (Vermögenswert, Entnahme) zugeordnet werden. Gesucht ist die Investition mit maximalem Zielwert. Unter Sicherheit reduziert sich das Investitionsproblem damit auf zwei Fragen: Welche Zielsetzung soll verfolgt werden und welche Kopplungen zu anderen Entscheidungsbereichen (Finanzierung, Programmplanung usw.) sind sinnvollerweise im Entscheidungsmodell abzubilden, um zu koordinierten Entscheidungen zu gelangen?
Bei unvollkommenen Informationen erweitert sich die Fragestellung. Die Entscheidungen binden Unternehmen i.d.R. für lange Zeit, und die ökonomischen Konsequenzen der Entscheidungen hängen davon ab, welche Umweltentwicklungen zukünftig eintreten werden. Über die künftigen Investitionsalternativen und Daten liegen aber nur unvollkommene Informationen vor. Die ökonomischen Konsequenzen einer Entscheidung lassen sich daher nicht eindeutig bestimmen. Der Planende muss sich aber trotzdem darüber klar werden, welche Maßnahmen ergriffen werden sollen.
Relevant wird die Unvollkommenheit des Entscheidungsfeldes erst, wenn negative Erfolgswirkungen durch Irreversibilität von Entscheidungen drohen (Jacob, 1967). Wenn ein Unternehmen Entscheidungen jederzeit ohne Nachteil (Verluste oder Anpassungskosten) revidieren kann, könnten Fehlentscheidungen schadlos korrigiert werden. Die Irreversibilität führt bei Unbestimmtheiten des Entscheidungsfeldes folglich zu Risiko, das in Entscheidungsmodellen erfasst werden muss.
2. Entscheidungsfeld bei unvollkommener Information
Reale Entscheidungsfelder zeichnen sich immer durch Offenheit aus: Es besteht unvollständige Kenntnis über die künftigen Handlungsmöglichkeiten, Wirkungszusammenhänge und Daten. Als Folge der unvollkommenen Informationen können die ökonomischen Wirkungen von Entscheidungen nur unvollständig beschrieben werden. Eine Optimierung im strengen Sinne ist unmöglich, da die Rückwirkungen der noch unbekannten Alternativen und Daten auf den Erfolg nicht erfasst werden können.
Trotz der Offenheit des Entscheidungsfeldes gehen betriebswirtschaftliche Modelle vereinfachend von geschlossenen Entscheidungsfeldern aus. Es wird angenommen, sämtliche Handlungsalternativen und Datensituationen seien bekannt. In derartigen Modellen wird damit von den realen Unbestimmtheiten weitgehend abstrahiert. Unvollständige Kenntnis existiert in diesen Modellen nur darüber, welche von mehreren möglichen Datensituationen tatsächlich eintreten wird. Dabei wird von folgender Annahme ausgegangen: Jeder Alternative ist in jeder Datensituation ein eindeutiger Erfolgswert zuzuordnen. Eine derartige Situation wird als Entscheidung unter Unsicherheit bezeichnet.
Bei Unsicherheit sind drei Situationen zu unterscheiden: Es lassen sich keine Eintrittswahrscheinlichkeiten für zukünftige Datensituationen angegeben (Ungewissheit). Im zweiten Fall sind dem Entscheidungsträger subjektive oder objektive Wahrscheinlichkeiten bekannt (Risiko). Denkbar ist auch, dass für die Eintrittswahrscheinlichkeiten nur Intervalle angegeben werden können.
Bei unvollkommener Information sind zwei Arten von Entscheidungen zu fällen (Adam, D. 1996):
| 1. | Für einen gegebenem Informationsstand sind Kriterien zu entwickeln, die es erlauben, Strategien als optimal zu identifizieren. Dabei kommt es darauf an, eine vernünftige Gewichtung von Risiko und Gewinn zu finden. | | 2. | Es muss geprüft werden, ob der Informationsstand verbessert werden kann und ob die neuen Informationen zu anderen Entscheidungen führen. Eine Informationsverbesserung ist nur dann sinnvoll, wenn der Nutzen der zusätzlichen Information die Kosten der Informationsbeschaffung übersteigt. |
3. Zielproblematik bei Unsicherheit
Ein Unternehmen kann zwar bei Unsicherheit nach maximalem Erfolg streben; der Erfolg hängt aber von der zufällig eintretenden Datensituation ab. Bei Unsicherheit ist eine Investition daher mit zwei Maßgrößen zu bewerten, einer für den Erfolg und einer zweiten für das Risiko. Beide Größen können in eine übergeordnete Nutzenfunktion integriert werden.
Für die Quantifizierung des Risikos existieren zwei Denkrichtungen. Einmal wird Risiko als Verlustgefahr definiert. In die Risikobewertung gehen dann nur Datensituationen ein, in denen eine Entscheidung zu Verlusten führt. Bei der zweiten Denkrichtung wird jede Abweichung vom erwarteten Erfolg als Risiko interpretiert. Auch positive Abweichungen (Chancen) werden in diesem Fall als Risiko angesehen. Das entspricht nicht dem in der Praxis üblichen Risikoverständnis.
Die zweite Denkrichtung misst Risiko in zwei Formen. Einmal wird die mittlere Abweichung des Erfolges einer Strategie vom Erwartungswert bestimmt (horizontale Messung). Bei vertikaler Messung wird die Abweichung der Erfolge einer Handlungsalternative in einer bestimmten Datensituation im Vergleich zu anderen Alternativen bestimmt. Die vertikale Messungsart ist problematisch; sie kann zu inkonsistenten Entscheidungen führen (Adam, D. 1996).
Bei unvollkommenen Informationen sind Investitionen zudem auf ihre Anpassungsfähigkeit zu beurteilen: Gesucht ist die Alternative, die nicht nur in der wahrscheinlichsten Datensituation zu hohem Erfolg führt, sondern die sich ohne hohe Anpassungskosten an andere Datensituationen anpassen lässt. Elastizität der Strategien ist im Allgemeinen nur durch Verzicht auf Erfolg in der wahrscheinlichsten Datensituation zu erkaufen. Für die Investitionspolitik ist daher ein „ Trade-off “ zwischen „ Erfolg “ und „ Anpassungsfähigkeit “ festzulegen.
1. Merkmale eines offenen Entscheidungsfelds
Investitionsentscheidungen sind zu treffen, obwohl unvollständige Kenntnis über die Handlungsalternativen und Datensituationen besteht. In einem geschlossenen Modell kann aber nur versucht werden, aus der Menge der bekannten Handlungsalternativen und Wirkungszusammenhänge die relativ beste Lösung zu finden. Es fragt sich, ob auch der noch unbekannte Teil des Entscheidungsfeldes in irgendeiner Form in die Planungsüberlegungen einbezogen werden kann. Dazu bestehen einige Ansätze (Schlüchtermann, 1996):
| - | Der technische Fortschritt wird in der Zukunft neue Investitionsalternativen hervorbringen, die heute noch unbekannt sind. In die Planung bei offenen Entscheidungsfeldern lassen sich allenfalls begründete Erwartungen über den Fortschritt (Kostensenkungspotenziale, Reduzierung des Faktoreinsatzes) einbeziehen. Auf Basis dieser Erwartungen wird dann u.U. eine heute verfügbare Ersatzmaschine nicht beschafft. | | - | Eine bereits diskutierte Reaktion auf die Offenheit des Entscheidungsfeldes besteht darin, für Anpassungsfähigkeit der Investitionsstrategien zu sorgen (Jacob, 1989). Die Bestands- und Entwicklungsflexibilität eines Unternehmens lässt sich z.B. durch Investitionen in anpassungsfähige Technologien (Flexible Fertigungssysteme) statt Spezialanlagen sicherstellen. | | - | Eine weitere Möglichkeit besteht darin, eine Investitionspolitik zu verfolgen, die künftig hinreichende finanzielle Potenziale (Kasse, Kreditlinie, Finanzanlagen) zur Anpassung des Unternehmens belässt. Das Unternehmen schöpft dann heute bestehende Finanzierungsgrenzen nicht voll aus. Das Gleiche kann erreicht werden, wenn das Unternehmen seiner Rechnung einen höheren Zins als den Marktzins zugrunde legt (Zinshürden). Für die Unternehmensleitung gilt es abzuwägen, ob der langfristige Erfolgsbeitrag der Potenziale am größten ist, wenn sie heute eingesetzt oder wenn sie für künftige Investitionen reserviert bleiben. |
2. Planungsmethoden in offenen Entscheidungsfeldern
Auch durch Planungsmethoden kann die Planung in offenen Entscheidungsfeldern unterstützt werden.
Für offene Probleme bietet es sich an, nur den Teil der Planungsergebnisse zu realisieren, der sich auf die erste Periode eines mehrperiodigen Planungszeitraums bezieht. Eine Periode später wird aufbauend auf dem Istzustand und den neu eingetreten Informationen ein Neuaufwurf der Planung durchgeführt. Durch diesen rollierenden Planungsmodus wird die Planung laufend an Verbesserungen des Informationsstandes angepasst.
Phantomvariable sind eine weitere Möglichkeit, zukünftige, heute noch unbekannte Alternativen in die Planung einzubeziehen. Dieses Konzept wird z.B. in der Theorie der optimalen Nutzungsdauer benutzt. Mangels besseren Wissens wird von einer unendlichen Wiederholung der gleichen Investitionen ausgegangen. Künftige Kettenglieder sind dann Phantomvariable mit identischen Zahlungsreihen wie die erste reale Investition. Auf diese Weise gelingt es, den grundsätzlichen Einfluss des Kapitalwertes der künftigen Kettenglieder auf die Nutzungsdauer des ersten Kettengliedes transparent zu machen.
Korrekturverfahren (Blohm, /Lüder, 1995) berücksichtigen die Unsicherheit durch pauschale Risikoabschläge oder -zuschläge bei den Daten (Zahlungen, Nutzungsdauer, Zinssatz). Dabei können einzelne Daten oder ganze Datensätze risikokorrigiert sein. Mit den korrigierten Daten wird wie mit sicheren Daten gerechnet. Je größer die Unsicherheit ist, desto stärker werden die Daten korrigiert. Eine Investition wird dann nur als vorteilhaft eingestuft, wenn sie den Zinssatz für risikolose Finanzanlagen zuzüglich eines angemessenen Risikoaufschlages erwirtschaftet. Die Verfahren geben keinen inhaltlichen Hinweis, in welchem Ausmaß die Daten zu korrigieren sind. Ihnen wohnt damit eine Willkür inne, die leicht zum “ Totrechnen “ von Projekten führen kann. Die benutzten Risikokorrekturen sind kaum sinnvoll interpretierbar, da das Risiko durch die meist nicht nachvollziehbaren individuellen Datenkorrekturen verdeckt wird.
Sensitivitätsanalysen (Albach, H. 1976; Blohm, /Lüder, 1995) beantworten die Frage, ob Entscheidungen bei bestimmten Veränderungen der Daten stabil bleiben. Zu bestimmen ist etwa das kritische Preisniveau von Produkten, bei dem bestimmte Absatzmengen zu einem positiven Kapitalwert führen. Es kann auch analysiert werden, wie sich Nutzungsdauer, Absatzmengen, Anschaffungsausgaben oder die laufenden Betriebsausgaben verändern dürfen, ohne dass die Vorteilhaftigkeit einer Investition in Frage gestellt ist. Kritische Werte geben damit einen Einblick in die Struktur und die Spielräume der Entscheidung.
III. Planungsmethoden in geschlossenen Entscheidungsfeldern
1. Merkmale einer Investitionsentscheidung unter Unsicherheit
Die Entscheidungstheorie geht von einem geschlossenen Entscheidungsfeld aus. Es ist dem Entscheidungsträger möglich, zustandsabhängige Erfolgsbeiträge für Investitionsprojekte in Form einer Entscheidungsmatrix anzugeben.
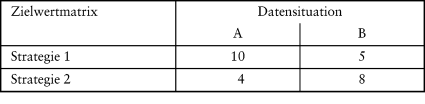
Damit existieren zwei Problembereiche. Zum einen ist festzulegen, wie die zustandsabhängigen Rückflüsse eines Zeitpunktes auf einen Zielwert zu verdichten sind; zum anderen muss festgelegt werden, wie zustandsabhängige Rückflüsse unterschiedlicher Zeitpunkte zu behandeln sind.
2. Bewertung einperiodiger Investitionsobjekte a) Das Erwartungswertkriterium
Die am häufigsten angewandte Entscheidungsregel ist die Maximierung des Erwartungswertes (Bamberg, /Coenenberg, 2000). Der Erwartungswert μi der Alternative i entspricht der Summe der mit den Wahrscheinlichkeiten wj gewichteten Erfolge Gij in den einzelnen Datensituationen j. Das Erwartungswertkriterium vernachlässigt Risikoaspekte vollständig; ein Entscheidungsträger stuft zwei Strategien mit gleichem Erwartungswert als gleichwertig ein, und zwar unabhängig von der Streuung der Erfolge. Eine sichere und eine unsichere Alternative werden bei gleichem Erwartungswert folglich als gleichwertig angesehen. Im Erwartungswertkriterium kommt damit eine indifferente Einstellung zum Risiko zum Ausdruck.
Das Erwartungswertkriterium ist damit streng genommen nur für häufig wiederkehrende Entscheidungen anwendbar. Nur bei häufiger Wiederholung strebt der mittlere Erfolg gegen den Erwartungswert, d.h., für die Summe der Investitionen gibt es kein Risiko. Jede einzelne Entscheidung ist aber mit Unsicherheit verbunden. Der Erwartungswert ist daher als Entscheidungskriterium für einmalige Investitionsentscheidungen risikoscheuer Entscheidungsträger äußerst kritisch zu beurteilen. b) Das Bernoulli-Prinzip
Einen formal ähnlichen Weg geht das Bernoulli-Prinzip. Es wird nicht der Erwartungswert des Erfolges, sondern der des Risikonutzens bestimmt. Mit einer für jeden Entscheidungsträger individuell zu bestimmenden Risikonutzenfunktion ist jedem möglichen Ergebniswert Gij ein Nutzen N(Gij) zuzuordnen. Die Nutzenwerte N(Gij) werden mit den Eintrittswahrscheinlichkeiten wj gewichtet und zum Erwartungswert des Nutzens summiert.
Die Art der Nutzenfunktion wird durch die individuelle Risikoneigung des Entscheidungsträgers bestimmt. Bei einer linearen Beziehung zwischen Nutzen und Gewinn besteht Risikoneutralität. Wächst der Nutzen unterproportional (überproportional) mit wachsendem Erfolg Gij, wird von Risikoscheu (Risikofreude) gesprochen. Für Investitionsentscheidungen sind insbesondere Funktionen bei Risikoscheu relevant.
Das Bernoulli-Prinzip überzeugt aufgrund der einzuhaltenden Axiome als formales Denkprinzip für Rationalverhalten (Bitz, 1981), ist aber nur unter starken Vorbehalten für praktische Investitionsentscheidungen einsetzbar, da risikoscheue Entscheidungsträger u.U. gegen die Prämissen des Prinzips verstoßen (Adam, D. 1996). c) Das μ-σ-Prinzip
Nach dem μ-σ-Prinzip wird jede Alternative durch zwei Kenngrößen, den Erwartungswert μ und die Standardabweichung σ, bewertet (Bitz, 1981). Eine Investition ist aus Sicht eines risikoscheuen Entscheidungsträgers einer anderen Alternative vorzuziehen, wenn sie bei gleicher Standardabweichung einen höheren Erwartungswert oder bei Gleichheit der Erwartungswerte eine niedrigere Standardabweichung besitzt. Gelingt es mit dieser Effizienzbetrachtung nicht, eine dominante Investition zu identifizieren, muss zusätzlich mit einer Nutzenfunktion gearbeitet werden, die aus beiden Kenngrößen gebildet wird. Die Nutzenfunktion definiert ein Austauschverhältnis zwischen μ und σ. Aus dieser Nutzenfunktion ergibt sich für jedes Nutzenniveau ein Sicherheitsäquivalent – der sichere Erwartungswert, der denselben Nutzen stiftet, wie eine unsichere Alternative. Das μ-σ-Prinzip transformiert die Entscheidung unter Risiko damit formal in eine Entscheidung unter Sicherheit. Als Rückfluss für eine Investition wird das Sicherheitsäquivalent angesetzt und mit dem Zinssatz für ein risikoloses Finanzgeschäft diskontiert. Das um Nutzenfunktionen erweiterte μ-σ-Prinzip wird z.B. in der Kapitalmarkttheorie im Rahmen der Portfolio Selection (Markowitz, 1959) und beim Capital Asset Pricing Model (CAPM) angewendet (Sharpe, 1970). d) Die Risikoanalyse
Die Risikoanalyse (Hertz, 1964) bietet die Möglichkeit, Investitionsobjekte durch Risikoprofile (kumulierte Wahrscheinlichkeiten für den Eintritt bestimmter Erfolge) zu beurteilen. Im Gegensatz zum μ-σ-Prinzip wird eine Investition damit nicht durch zwei Kennwerte sondern durch eine ganze Wahrscheinlichkeitsverteilung der Erfolgsgröße dargestellt.
Um das Risikoprofil einer Strategie abzuleiten, ist aus den Wahrscheinlichkeitsverteilungen der Daten eine Dichtefunktion der Erfolgsgröße (z.B. Kapitalwert) zu entwickeln, die dann in das Profil transformiert wird. Für diese Ableitung wird auf Simulationen zurückgegriffen. Auf der Basis des für einzelne Investitionen bestimmten Profils kann anschließend eine Entscheidung gefällt werden, indem die Profile alternativer Strategien miteinander verglichen werden. Ist der Kapitalwert einer Investition für jede Wahrscheinlichkeit des Profils größer als der einer zweiten Investition, dominiert die erste die zweite Investition. Schneiden sich die Profile zweier Investitionen, kann z.B. jene Investition gewählt werden, bei der ein bestimmter Mindestkapitalwert mit der höchsten Wahrscheinlichkeit realisiert wird (Adam, D. 1996).
Mit der Dichtefunktion der Erfolgsgröße stellt die Risikoanalyse Informationen bereit, die auch für Entscheidungen nach klassischen Prinzipien wie μ und μ-σ erforderlich sind, denn ohne Kenntnis der Wahrscheinlichkeitsverteilung für die Erfolgsgrößen lassen sich weder Erwartungswerte noch Standardabweichungen bestimmen. Die Risikoanalyse ermöglicht es zudem, eine große Anzahl unsicherer Inputinformationen und sich daraus ergebender alternativer Zukunftslagen in die Planung einzubeziehen. Probleme ergeben sich durch den vergleichsweise hohen Berechnungsaufwand, der durch stochastische Abhängigkeiten zwischen den Inputgrößen noch erhöht werden kann. Daher wird eine künstliche Beschränkung der zu analysierenden Datensituationen vorgeschlagen. Für jede Inputgröße werden z.B. nur drei Ausprägungen (pessimistischer, optimistischer, wahrscheinlichster Wert) zugelassen. Die Simulation liefert dann nur einen groben Schätzwert für das Risikoprofil. e) Mathematische Programmierung
Die Verfahren der stochastischen Optimierung versuchen, deterministische Ansätze der simultanen Investitions- und Finanzplanung auf den Unsicherheitsfall zu übertragen. Damit können Unvollkommenheiten der Kapitalmärkte und die daraus resultierenden Interdependenzen im Kalkül berücksichtigt werden. Beim Chance-Constrained-Programming (Charnes, /Cooper, 1960) wird z.B. der Erwartungswert der Zielgröße unter einem Satz von Nebenbedingungen (z.B. für die Liquidität) maximiert. Diese Restriktionen sind mit einer vorzugebenden Wahrscheinlichkeit einzuhalten. Zur Lösung werden die Wahrscheinlichkeitsrestriktionen in deterministische Äquivalente umgeformt. Bei diesem Verfahren bleibt völlig offen, welche ökonomischen Folgen eine Verletzung der Nebenbedingungen hat und wie die Wahrscheinlichkeiten für die einzuhaltenden Restriktionen gewählt werden sollen (Blohm, /Lüder, 1995).
3. Bewertung mehrperiodiger Investitionsobjekte a) Berücksichtigung von Zeit- und Risikoaspekten
Für die Beurteilung mehrperiodiger Investitionsobjekte ist neben den Risikoaspekten auch der zeitliche Anfall der Zahlungen zu berücksichtigen. Dies kann grundsätzlich auf zwei Arten geschehen (Fischer, 1999):
Zum einen kann der Kalkulationszinsfuß um einen Risikokorrekturfaktor modifiziert werden. In diesem Fall sind in der Zahlungsreihe des Objektes z.B. die Erwartungswerte der Zahlungsüberschüsse in den einzelnen Zeitpunkten t anzusetzen, die mit risiko- und laufzeitabhängigen Zinssätzen zu diskontieren sind.
Zum anderen kann versucht werden, die Erwartungswerte der Rückflüsse in den einzelnen Zeitpunkten um einen Betrag zu korrigieren, der das investitionsspezifische Risiko abbildet. An die Stelle der unkorrigierten Erwartungswerte treten dann die Sicherheitsäquivalente, die mit den laufzeitabhängigen Marktzinssätzen für sichere Zahlungen diskontiert werden.
In einem mehrperiodigen Investitionsmodell ist zudem die Entwicklung des Informationsstands im Zeitablauf abzubilden; d.h., es sind Informationsverbesserungen zu erfassen, die sich im Zeitablauf einstellen. In einem geschlossenen Entscheidungsfeld können derartige Informationsverbesserungen nicht daraus resultieren, dass neue, bisher unbekannte Datensituationen hinzutreten. Die Informationsverbesserungen äußern sich allein darin, dass die Zahl der zukünftig möglichen Datensituationen im Zeitablauf immer enger eingegrenzt werden kann. Die Entwicklung der Informationen im Zeitablauf kann durch eine Informationsstruktur visualisiert werden.
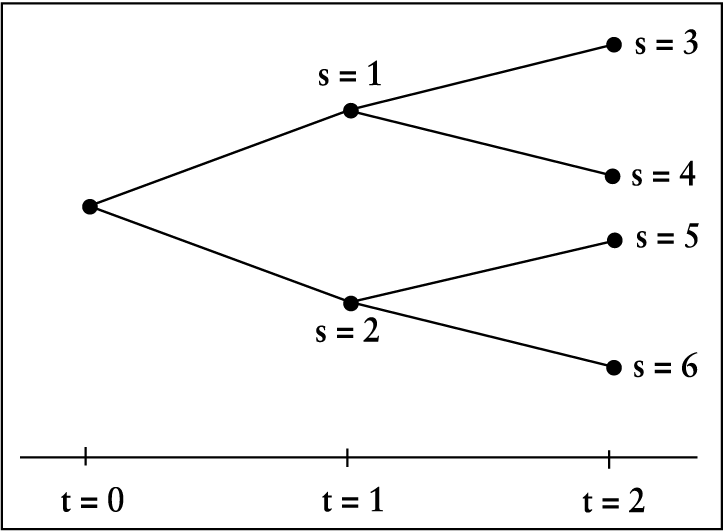
Abb. 2: Informationsstruktur
Aus der Sicht des Zeitpunktes t = 0 sind sechs zukünftige Umweltzustände möglich. Ist eine Periode vergangen und der Zustand s = 1 eingetreten, reduziert sich das Problem auf zwei mögliche Zustände für t = 2. b) Starre versus flexible Planung
Planungsverfahren in geschlossenen Entscheidungsfeldern bei Unsicherheit lassen sich danach differenzieren, inwieweit zukünftige Informationsverbesserungen in der Planung berücksichtigt werden. Eine Planung, die im Planungszeitpunkt nicht bereits für alle Teilperioden die optimale Verhaltensweise definitiv festlegt, sondern für zukünftige Zeitpunkte nur optimale Eventualstrategien formuliert, wird als flexible Planung (Hax, 1985) bezeichnet. Der Entscheidungsträger reagiert auf die Datenunsicherheit durch ein flexibles Entscheidungsverhalten. Zeitlich aufeinander folgende, im Erfolg aber interdependente Entscheidungen werden nicht als einstufige, sondern als mehrstufige Entscheidungen aufgefasst. Durch die Formulierung bedingter Strategien besteht in zukünftigen Perioden noch Entscheidungsfreiheit.
Bei starrer Planung wird bereits im Kalkulationszeitpunkt das gesamte künftige Handeln festgelegt. Somit erfasst die starre Planung nicht die Möglichkeit, Entscheidungen auf künftige Perioden aufzuschieben. Weil die starre Planung keine Eventualstrategien berücksichtigt, erfasst sie grundsätzlich weniger Handlungsalternativen als eine flexible Planung. Da das Entscheidungsfeld enger definiert ist, kann der optimale Plan bei starrer Planung von dem der flexiblen Planung abweichen. Eine flexible Planung ist grundsätzlich sachlich richtiger, da sie von einem umfassenderen Entscheidungsfeld ausgeht. Die erhöhte Planungsgenauigkeit wird aber durch eine starke Ausweitung der Strategien erkauft. Der Planungsaufwand steigt schnell in nicht mehr beherrschbare Größenordnungen an. Flexible Planung bietet sich daher in der Realität nur an, wenn die Zahl bedingter Strategien klein gehalten werden kann. Flexible Planung ist somit eher ein Denkprinzip als ein praktisch einsetzbares Verfahren.
IV. Kapitalmarktorientierte Bewertung unsicherer Investitionen
1. Arbitragefreier Kapitalmarkt bei Unsicherheit a) Grundlagen arbitragefreier Bewertung
Versuche, den Zielkonflikt zwischen Erfolg und Risiko durch eine Nutzenfunktion zu überwinden, haben den großen Nachteil, dass sich diese Funktion nur schwer bestimmen lässt. Zudem sind die Ergebnisse der Planung nicht interpersonell nachvollziehbar, da jeder Entscheidungsträger von einer anderen Nutzenfunktion ausgeht. Investitionsentscheidungen weisen somit eine gewisse Beliebigkeit auf. Eine Möglichkeit, Objektivität zu erreichen, liegt darin, auf die Daten des Kapitalmarktes zurückzugreifen. In den Marktpreisen der Wertpapiere spiegeln sich die heutigen und zukünftigen Erwartungen der Investoren sowie ihre Risikovorstellungen wider. Die kapitalmarktorientierte Bewertung unsicherer Investitionen geht von vollständigen und arbitragefreien Märkten aus und fragt, ob Sachinvestitionen besser sind als eine alternative Anlage auf dem Kapitalmarkt. Die arbitragefreie Bewertung von Investitionen versucht damit eine Integration von Investitions- und Kapitalmarkttheorie. Dieser Ansatz unterstellt, dass jeder Investor uneingeschränkten Zugang zum Kapitalmarkt hat.
Auf dem Kapitalmarkt werden diverse Finanzierungstitel gehandelt, die Ansprüche auf sichere oder unsichere Zahlungen verbriefen. Dieser Kapitalmarkt muss folgende Eigenschaften besitzen (Franke, /Hax, 1999; Kruschwitz, 1999):
| - | Für die Zukunft werden S Datensituationen für möglich gehalten. Diese Zustände sind eindeutig und vollständig definiert (geschlossenes Entscheidungsfeld), und die Eintrittswahrscheinlichkeit jedes Zustands s ∊ S ist positiv. Die Informationsstruktur des Marktes wird z.B. durch den oben abgebildeten Zustandsbaum visualisiert. | | - | Alle Marktteilnehmer haben die gleichen Erwartungen über die zustandsabhängigen Rückflüsse der Finanztitel. Jedem Titel wird damit für jeden Umweltzustand ein eindeutiger Rückfluss zugeordnet. | | - | Die Completeness-Annahme besagt: Am Markt werden mindestens so viele Titel gehandelt wie Umweltzustände definiert wurden. Der Markt ist vollständig. | | - | Der Kapitalmarkt ist atomistisch. Einzelne Handlungen haben keinen Einfluss auf das Preissystem. | | - | Transaktionen auf dem Kapitalmarkt vollziehen sich reibungslos, es gibt keine Transaktionskosten. | | - | Es gibt keine Informationsineffizienzen. Alle Marktteilnehmer verfügen über die gleichen Informationen. |
Sind diese Bedingungen erfüllt und handeln alle Marktteilnehmer rational, stellen sich auf dem Markt Gleichgewichtspreise ein. Im Gleichgewicht kann kein Marktteilnehmer durch eine Kombination von Finanzgeschäften zusätzliche Einzahlungen in mindestens einem Zustand erwirtschaften, ohne dafür gleichzeitig Auszahlungen zu leisten. Der Markt ist in diesem Fall arbitragefrei; es existiert für alle auf dem Kapitalmarkt gehandelten Finanztitel ein eindeutiges Preissystem, welches jedem Titel einen fairen Marktpreis zuordnet. b) Ermittlung fairer Marktpreise für unsichere Zahlungen
Gegeben sei ein Kapitalmarkt mit sechs Zuständen, auf dem sechs Finanztitel mit unsicheren Rückflüssen und einer Restlaufzeit von zwei Jahren gehandelt werden.
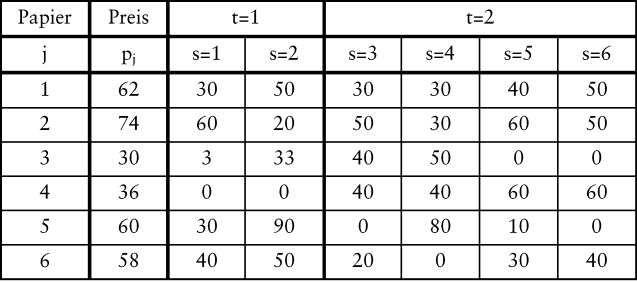
Abb. 3: Gehandelte Wertpapiere
Für diesen Kapitalmarkt lässt sich unter obigen Prämissen folgendes Gleichungssystem aufstellen:
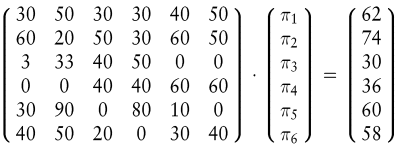
Die Variablen πs bezeichnen die Gewichte, mit denen die Zahlungen in den sechs Zuständen zu multiplizieren sind, um den heutigen Kurs der Titel zu erklären. Diese Gewichte bringen zum Ausdruck, welchen Wert ein Investor einer künftigen Zahlung von einer Geldeinheit im Zustand s heute zumisst (Arrow, K.J. 1970; Debreu, 1959). Dieser Zusammenhang wird deutlich, wenn obiges Gleichungssystem mit der Inversen der Zahlungsmatrix multipliziert wird (Kruschwitz, 1999):
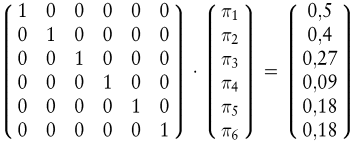
Durch diese Umformung wird ein Markt konstruiert, auf dem fiktive Finanztitel gehandelt werden, die ausschließlich im Zustand s einen Anspruch auf Zahlung einer Geldeinheit verbriefen. Diese konstruierten Titel werden als reine Wertpapiere bezeichnet (Kruschwitz, 1999; Myers, 1968). Die sechs real am Markt gehandelten Wertpapiere können als Kombinationsgeschäfte aus reinen Wertpapieren interpretiert werden. Die Preise πs reiner Wertpapiere erklären dann die Kurse pj der realen Finanztitel j. Dazu sind die Rückflüsse Xjs eines Titels j im Zustand s mit den Preisen reiner Wertpapiere zu multiplizieren:
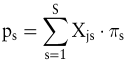
Um für einen unsicheren Zahlungsstrom Preisentwicklungen im Zeitablauf bestimmen zu können, ist die Veränderung der Informationsstruktur zu berücksichtigen. Zur Bestimmung künftiger Preise ist damit relevant, welche Zustände in zukünftigen Zeitpunkten eintreten. Das soll an einem Beispiel verdeutlicht werden:
Ein Wertpapier A verspricht im Zeitpunkt t=2 zustandsabhängige Zahlungen von (40; 80; 100; 50). Wird das Papier mit den Preisen reiner Wertpapiere bewertet, ergibt sich ein heutiger fairer Preis von 45 GE. Im folgenden wird der Preis in t=1 auf Basis der dann gültigen Informationsstruktur ermittelt. Da nach Ablauf der ersten Periode in t=1 zwei Zustände eingetreten sein können (s=1 oder s=2), empfiehlt sich eine Teilung des Wertpapiers A in zwei fiktive Papiere A* und A**. Das Papier A* (A**) verbrieft Zahlungen, wenn im Zeitpunkt t=1 der Zustand s=1 (s=2) eingetreten ist. Papier A* führt dann in t=2 zu Zahlungen von (40; 80; 0; 0), und Papier A** zu Zahlungen von (0; 0; 100; 50). Aus dem Preissystem des Kapitalmarktes ergibt sich für A* ein heutiger Marktwert von 18 GE:

Um den zukünftigen Preis des Wertpapiers A* im Zeitpunkt t=1 zu bestimmen, ist zu fragen, welche Zahlung P im Zustand s=1 einem heutigen Preis von 18 GE entspricht. Über die Definition des Wertpapiers A* ist dieser Preis P gleich dem zukünftigen Preis pA,t=1|s=1 des Papiers A. Formal bedeutet dies:
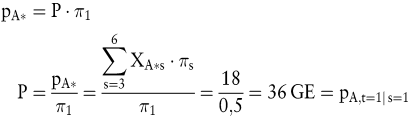
Falls in t=1 der Zustand s=1 eintritt, ist für das Wertpapier A ein künftiger Preis von 36 GE zu zahlen. In analoger Weise kann der zukünftige Preis des Wertpapiers A bestimmt werden, wenn in t=1 Zustand s=2 eintritt. Für s=2 ergibt sich in t=1 ein Preis von 67,5 GE. Werden beide zustandsabhängigen zukünftigen Preise des Wertpapiers A mit den Preisen reiner Wertpapiere bewertet, ergibt sich wieder der heutige Preis von 45 GE.
Analog sind auch die künftigen Preise reiner Wertpapiere zu bestimmen. Tritt im Zeitpunkt t der Zustand s* – z.B. s=1 – ein, entspricht der zukünftige Preis eines reinen Wertpapiers, das nur im Zustand Zustand s+einen Rückfluss von einer GE verbrieft, dem Ausdruck:

Allgemein kann damit der künftige Preis eines Wertpapiers unter der Voraussetzung, dass im Zeitpunkt t der Zustand s* eingetreten ist, wie folgt bestimmt werden:
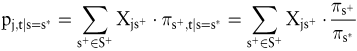
Als Folge dieses Zusammenhanges lassen sich die künftigen Kurse der Wertpapiere auf einem arbitragefreien Markt aus den heutigen Kursen ableiten. Dieser Zusammenhang gilt grundsätzlich nur in einem geschlossenen Entscheidungsfeld. Der zeitliche Zusammenhang der Kurse existiert nur, weil mit dem Zeitablauf keine neuen Datensituationen hinzutreten können. c) Determinanten der Preise zustandsabhängiger Zahlungen
Die Preise reiner Wertpapiere πs geben an, welcher Preis im Zeitpunkt t=0 für ein Wertpapier mit einem Anspruch auf Zahlung einer Geldeinheit im Zustand s geleistet wird, wenn in allen anderen Zuständen kein Rückfluss erwartet wird (Arrow, K.J. 1970; Debreu, 1959). Werden mit Hilfe dieser Preise die Marktwerte beliebiger Zahlungsströme bestimmt, sind explizit weder Zeitpräferenzen noch Eintrittswahrscheinlichkeiten für die Umweltzustände noch Risikopräferenzen der Investoren zu berücksichtigen. Diese sind implizit in den Preisen reiner Wertpapiere enthalten.
Steigt ceteris paribus die Wahrscheinlichkeit für den Umweltzustandes s=3, steigt auch der Marktpreis für den Anspruch auf Zahlung einer Geldeinheit in diesem Zustand und damit der Wert von π3. In bezug auf den sicheren Zins werden Projekte um so besser beurteilt, je kleiner der sichere Zins ist. Dies ist ohne Einschränkungen auch auf den Fall der Unsicherheit übertragbar.
2. Kapitalmarktorientierte Investitionsbewertung a) Entscheidungsfeld und Zielsetzung
Im Folgenden wird die arbitragefreie Bewertung auf Investitionsentscheidungen übertragen. Dazu wird eine Kapitalgesellschaft betrachtet, die einen uneingeschränkten Zugang zum vollkommenen Kapitalmarkt hat. Das Unternehmen kann zu den Konditionen des Marktes unbeschränkt Finanzinvestitionen tätigen und Kredite aufnehmen. Zusätzlich besteht die Möglichkeit, verschiedene unabhängige Realinvestitionsprojekte i mit zustandsabhängigen Rückflüssen Xis zu realisieren. Auch für die Kapitalgeber wird ein uneingeschränkter Zugang zum Kapitalmarkt unterstellt. Sie können eventuelle Ausschüttungen zu den Konditionen des Marktes anlegen.
In dieser Situation bilden die Preise reiner Wertpapiere die Opportunität sowohl des Unternehmens als auch der Anteilseigner ab. Für die Beurteilung der Sachanlagen ist zu fragen, ob mit ihnen mehr zu verdienen ist als auf dem Kapitalmarkt. b) Investitionsentscheidungen
Im folgenden werden drei Typen von Entscheidungen betrachtet, Vorteilhaftigkeitsprobleme, Wahlvergleiche und die Bewertung flexibler Strategien.
Wenn zwischen den Investitionsprojekten keine Interdependenzen bestehen und auf dem Kapitalmarkt keine Restriktionen existieren, können die Investitionen isoliert beurteilt werden (Adam, D. 2000). Ein Projekt ist vorteilhaft, wenn sein Kapitalwert auf Basis der Marktpreise positiv ist.
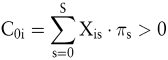
Diese Formel entspricht formal der klassischen Kapitalwertmethode. An die Stelle der Abzinsungsfaktoren sind lediglich die Marktpreise reiner Wertpapiere getreten. Im einfachsten Fall – Sicherheit – entsprechen die Marktpreise dem Ausdruck 1/(1+r)-t. Für einen sicheren Zins von r=10% mit dem Abzinsungsfaktor 1,1 – 1 ergibt sich z.B. der Ausdruck π1 = 0,90909. Die klassische Kapitalwertmethode ist damit ein Spezialfall der arbitragefreien Bewertung von Investitionen. Im Unsicherheitsfall bilden die Marktpreise neben dem Marktzins auch die Eintrittswahrscheinlichkeit und die Risikoeinstellung der Marktteilnehmer ab.
Stehen mehrere funktionsgleiche Investitionen zur Wahl, ist das Projekt mit dem höchsten positiven Kapitalwert zu wählen. Über etwaige Differenzinvestitionen muss nicht nachgedacht werden, weil unterstellt wird, dass diese Differenzen zu den Konditionen des Kapitalmarktes angelegt werden.
Der bisherigen Betrachtung lag eine starre Strategie zugrunde. Über die gegebene Informationsstruktur wurden zwar unsichere Erwartungen berücksichtigt, Anpassungsspielräume an eine sich verändernde Informationslage wurden aber nicht erfasst. Diese Handlungsspielräume gleichen einer Option, sich an mögliche Umweltbedingungen anzupassen (Myers, 1977). Beispielsweise steht ein Unternehmen in t=0 vor der Wahl, die Investition sofort zu tätigen oder um ein Jahr zu verschieben. Es muss dann den Vorteil sofortiger Investition gegen den Vorteil einer späteren Investition abwägen. Optionscharakter hat auch eine Erweiterungsinvestition, bei der der Investor aus einer künftigen Kapazitätserweiterung zusätzliche Rückflüsse erwirtschaftet. Die Option ist in die heutige Investitionsentscheidung zu integrieren.
Optionen können grundsätzlich den Wert einer Basisinvestition vergrößern. Werden sie nicht im Kalkül erfasst, kommt es zu einer systematischen Fehlschätzung der Erfolgswirkungen. Als Folge werden vorteilhafte Investitionen u.U. nicht getätigt.
Wie Realoptionen über die Bewertung mit Preisen reiner Wertpapiere berücksichtigt werden können, soll an einem Beispiel mit folgender Zahlungsreihe gezeigt werden: 
Abb. 4: Zahlungsreihe der Investition
Im Zeitpunkt t=1 bestehe die Möglichkeit einer Erweiterungsinvestition mit einer Auszahlung von 20 GE. Diese Investition führe zu einer Verdoppelung der in t=2 erwarteten Einzahlungsüberschüsse. Für die Basisinvestition ergibt sich aus dem bisherigen Preissystem reiner Wertpapiere ein Kapitalwert von -2 GE.
Dieser Marktwert berücksichtigt den Wert der Erweiterungsmöglichkeit nicht. Die Erweiterung ist als europäische Kaufoption aufzufassen. Es besteht ein Recht, aber keine Pflicht, die Erweiterungsinvestition auszuüben. Das Unternehmen wird die Option ausüben, wenn der Wert der zusätzlichen Rückflüsse zum Zeitpunkt t=1 größer ist, als die Anschaffungsausgabe von 20 GE, ansonsten wird die Option verfallen. Ist in t=1 der Zustand s=1 eingetreten, lässt sich der Marktwert der Option O durch folgende Gleichung bestimmen:
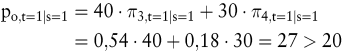
Tritt in t=1 hingegen der Zustand s=2 ein, lässt sich in analoger Weise ein künftiger Marktwert pO,t=1|s=2 von 11,25 bestimmen. Unter der Prämisse eines rationalen Entscheiders wird die Erweiterung nur durchgeführt, wenn der Wert der zusätzlich erzielbaren Rückflüsse in t=1 größer ist als die Auszahlung von 20 GE.
Die Option auf die zusätzlichen Rückflüsse führt im Beispiel zu einem zusätzlichen Marktwert in t=1 von 27 – 20=7 GE. Tritt der Zustand s=2 ein, verfällt die Option. Der Optionswert ist dann null.
Auf den Zeitpunkt t=0 bezogen ergibt sich für die Option damit ein Marktwert von 7 · 0,5 + 0 · 0,4 =3,5 GE. Die Basisinvestition zuzüglich des Wertes der Erweiterungsoption hat damit einen Marktwert von 1,5 GE. Die flexible Investitionsstrategie ist also vorteilhaft.
3. Kritik
Eine kapitalmarktorientierte Bewertung von Investitionen objektiviert das Kalkül im Vergleich zu einer Rechnung mit individuellen Nutzenfunktionen. Die Entscheidung wird nachvollziehbar, da transparent wird, wie die in der Rechnung benutzte Opportunität zustande kommt. Als Folge des Konstruktes eines arbitragefreien Marktes werden aber keine Interdependenzen zwischen Investition und Finanzierung berücksichtigt. Die kapitalmarktorientierte Bewertung erlaubt daher eine isolierte Beurteilung von Investitionen mit Partialmodellen.
Die Vorteile beschreiben aber gleichzeitig die Nachteile. Sie resultieren aus der Prämisse eines geschlossenen Entscheidungsmodells und den Konstruktionsprinzipien des arbitragefreien Kapitalmarktes.
Ein positiver Kapitalwert kann sich für Sachinvestitionen nur ergeben, wenn zwar der Kapitalmarkt vollkommen ist, für den „ Markt “ der Sachinvestitionen diese Voraussetzung aber nicht gilt. Gäbe es auch für die Sachinvestitionen einen vollkommenen Markt, würden die Kapitalwerte der Sachinvestitionen über den Preismechanismus abgeschöpft, denn jeder positive Kapitalwert beschreibt eine Arbitragemöglichkeit. Das Modell wendet daher das Preissystem eines vollkommenen Teilmarktes auf den Gesamtmarkt an. Die Unsicherheiten für Sachinvestitionen stammen aber aus ganz anderen Quellen als die für Finanzgeschäfte. Sie resultieren bei Sachinvestitionen z.B. aus den Unsicherheiten regionaler Absatzmärkte. Wenn diese Unsicherheiten für Kapitalmarktpapiere nicht existieren, repräsentiert das Preissystem der Finanzmärkte auch nicht die Risikosituation der individuellen Sachanlagen. Damit dürfte in der Regel die Completeness-Prämisse nicht erfüllt sein. Anders formuliert: Es fehlen die für die Risikosituation der Sachinvestitionen relevanten reinen Wertpapiere.
Ein zweiter Nachteil resultiert aus der Vollkommenheitsprämisse für den Kapitalmarkt. Der in der Realität unvollkommene Markt führt dazu, dass Interdependenzen zwischen Investition und Finanzierung bestehen, die keine isolierte Beurteilung der Projekte erlauben. Als Folge der Unvollkommenheiten werden die zur Beurteilung einer Investitionen relevanten Opportunitäten nicht durch den vollkommenen Kapitalmarkt, sondern durch das finanziell eingeengte Entscheidungsfeld bestimmt (Adam, D. 2000). Nicht allein die Finanzkonditionen, sondern zusätzlich die Realverzinsungen der Sachanlagen haben dann Lenkeigenschaft.
Ein dritter Problembereich resultiert aus der geschlossenen Sichtweise des Entscheidungsfeldes. Real lassen sich die morgen geltenden Preise auf den Kapitalmärkten nicht aus den heutigen Kursen ableiten. In der Realität treten laufend neue Informationen über Entscheidungsalternativen und Daten hinzu. Dann aber lässt sich kein arbitragefreies Preissystem bestimmen, da die Entscheidungsträger unterschiedliche Vorstellungen und Erwartungen über die künftigen Veränderungen des Entscheidungsfeldes haben. Ein Entscheidungsträger muss dann seine individuellen Zukunftserwartungen in die Investitionsüberlegungen einbeziehen.
4. Ausblick
Trotz der skizzierten Kritikpunkte liefert die arbitragefreie Bewertung Anhaltspunkte für die Bewertung von Investitionen bei Unsicherheit.
Die Praktikabilität des Modells kann verbessert werden, wenn durch eine Szenarioplanung die Zahl der Zustände reduziert wird. Eine weitere Möglichkeit, die Praktikabilität zu erhöhen, besteht darin, mit normalverteilten Rückflüssen zu arbeiten. In diesem Fall müssen nicht alle Umweltzustände explizit formuliert werden; die Kenntnis von Erwartungswert und Standardabweichung der Rückflüsse reicht zur Beschreibung der Rückflüsse aus. Diese auf dem μ-σ-Prinzip aufbauende Vorgehensweise liegt z.B. dem CAPM zugrunde.
Weitere Entwicklungen, die auf die arbitragefreie Bewertung zurückzuführen sind und die Bewertung flexibler Strategien in den Vordergrund stellen, sind zeitstetige Modelle auf Basis der Contingent-Claim-Analysis und der Optionspreistheorie (Black, /Scholes, 1973; Trigeorgis, 1996).
Des Weiteren ist es möglich, das Modell durch die Definition zustandsbezogener Liquiditätsrestriktionen auch auf den Fall unvollkommener Märkte auszudehnen. Neben das Preissystem des Kapitalmarktes treten dann aus den Sachanlagen abgeleitete Lenkpreise, die die Marktpreise u.U. ersetzen (Adam, D. 2000; Laux, 1969).
Die arbitragefreie Bewertung kann damit als Grundmodell einer Investitionsrechnung in geschlossenen Entscheidungsfeldern angesehen werden, das in unterschiedlichste Richtungen weiterentwickelt werden kann. Realitätsnähe erhält ein solches Modell aber erst, wenn auch Aspekte eines offenen Entscheidungsfeldes und des unvollkommenen Kapitalmarktes berücksichtigt werden.
Literatur:
Adam, D. : Planung und Entscheidung, 4. A., Wiesbaden 1996
Adam, D. : Investitionscontrolling, 3. A., München et al. 2000
Albach, H. : Investitionsrechnungen bei Unsicherheit, in: HWF, hrsg. v. Büschgen, H.E., Stuttgart 1976, Sp. 893 – 908
Arrow, K.J. : Essays in the Theory of Risk-Bearing, Amsterdam 1970
Bamberg, G./Coenenberg, A. G. : Betriebswirtschaftliche Entscheidungslehre, 10. A, München 2000
Bitz, M. : Entscheidungstheorie, München 1981
Black, F./Scholes, M. : The Pricing of Options and Corporate Liabilities, in: JPol.E 1973, S. 637 – 659
Blohm, H./Lüder, K. : Investition, München 1995
Charnes, A./Cooper, W. W. : Chance-Constrained Programming, in: Man.Sc. 1960, S. 73 – 79
Debreu, G. : Theory of Value, New Haven 1959
Fischer, E. O. : Die relevanten Kalkulationszinsfüße in der Investitionsplanung, in: ZfB 1999, Jg. 69, S. 777 – 801 1999
Franke, G./Hax, H. : Finanzwirtschaft des Unternehmens und Kapitalmarkt, 4. A., Berlin et al. 1999
Hax, H. : Investitionstheorie, 5. A., Würzburg et al. 1985
Hertz, D. B. : Risk Analysis in Capital Investment, in: HBR 1964, S. 95 – 106
Jacob, H. : Zum Problem der Unsicherheit bei Investitionsentscheidungen, in: ZfB 1967, S. 153 – 187
Jacob, H. : Flexibilität und ihre Bedeutung für die Betriebspolitik, in: Integration und Flexibilität, hrsg. v. Adam, D. et al., Wiesbaden 1989, S. 15 – 60
Kruschwitz, L. : Finanzierung und Investition, 2. A., München et al. 1999
Laux, H. : Flexible Planung des Kapitalbudgets mit Hilfe der linearen Programmierung, in: ZfbF 1969, S. 728 – 742
Markowitz, H. M. : Portfolio Selection, New York 1959
Myers, S. C. : A Time-State-Preference Model of Security Valuation, in: JFin. Quant. Anal. 1968
Myers, S. C. : Determinants of Corporate Borrowing, in: JFE 1977, S. 147 – 175
Schlüchtermann, J. : Planung in zeitlich offenen Entscheidungsfeldern, Wiesbaden 1996
Sharpe, W. F. : Portfolio Theory and Capital Markets, New York et al. 1970
Trigeorgis, L. : Real Options: Managerial Flexibility and Strategy in Resource Allocation, Cambridge 1996
|