|
Investitionsrechenverfahren
Inhaltsübersicht
I. Einführung
II. Kapitalwertmethode
III. Methode des internen Zinsfußes
IV. Berücksichtigung von Unsicherheit und CAPM
V. Berücksichtigung von Handlungsspielräumen und Realoptionen
I. Einführung
Investitionsrechenverfahren sind Methoden zur finanzwirtschaftlichen Beurteilung von Investitionsprojekten. Da die Beurteilung von Investitionsalternativen ein komplexes Problem darstellt, werden vereinfachende Annahmen getroffen, die der Verdeutlichung der Grundprinzipien der Investitionsbeurteilung dienen. In Anlehnung an die Literatur wird unterstellt, der Kapitalmarkt sei „ vollkommen “ . Dies beinhaltet unter anderem, dass keine Steuern und Transaktionskosten anfallen, Wertpapiere beliebig teilbar sind und Eigentümer (Gesellschafter) alle Kapitalmarkttransaktionen zu denselben Konditionen wie Unternehmen tätigen können.
Die Art der Finanzierung eines Investitionsprojekts ist unter diesen Bedingungen irrelevant. Schließen sich Investitionsprojekte gegenseitig aus, so sind technische Gründe verantwortlich, nicht aber fehlende Finanzierungsmittel, da Kapital zur Finanzierung lohnender Investitionen am Kapitalmarkt immer aufgenommen werden kann. In diesem Fall sind die maßgeblichen Fragen, (1) welche Investitionsprojekte sich lohnen und durchgeführt werden sollen (Akzeptanzentscheidung) und (2) welches Investitionsprojekt am vorteilhaftesten ist, wenn sich mehrere lohnende Investitionsprojekte gegenseitig ausschließen (Auswahlentscheidung). Bei Existenz eines vollkommenen und zugleich vollständigen Kapitalmarkts können diese Fragen unabhängig von den Konsumpräferenzen und dem Grad der Risikoaversion der Eigentümer entschieden werden; das finanzwirtschaftliche Ziel ist die Maximierung des Vermögens der Eigentümer eines Unternehmens. Die in diesem Beitrag dargestellten Investitionsrechenverfahren zeigen auf, wie vor diesem Hintergrund die beiden Fragen beantwortet werden können. So genannte statische Verfahren werden also nicht berücksichtigt.
II. Kapitalwertmethode
Das wichtigste Verfahren zur Beurteilung von Investitionsprojekten ist die Kapitalwertmethode (Barwertmethode). Diese Methode wird im Folgenden zunächst für den Fall sicherer Erwartungen dargestellt.
Ein Investitionsprojekt sei mit Ein- und Auszahlungen in den Zeitpunkten t = 1 bis n verbunden. Zt ist der im Zeitpunkt t anfallende Einzahlungsüberschuss. Die Durchführung des Investitionsprojekts ist mit einer Anschaffungsauszahlung in Höhe von A0 im Zeitpunkt 0 (heute) verbunden. Auf dem Kapitalmarkt kann jederzeit (risikofreies) Kapital zum Einheitszinssatz rf für eine Periode angelegt oder aufgenommen werden. Eine Kapitalanlage(-aufnahme) im Zeitpunkt 0 in Höhe von X für t Perioden führt daher zu einer Einzahlung (Auszahlung) von 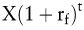 im Zeitpunkt t. Entsprechend hat eine (Nullkupon-)Anleihe, die im Zeitpunkt t zu einer Zahlung in Höhe von X führt, heute einen Preis (Wert) von im Zeitpunkt t. Entsprechend hat eine (Nullkupon-)Anleihe, die im Zeitpunkt t zu einer Zahlung in Höhe von X führt, heute einen Preis (Wert) von 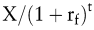 . .
Zur Beantwortung der Frage, ob sich die Durchführung eines Investitionsprojekts lohnt, muss geprüft werden, welcher Betrag alternativ am Kapitalmarkt anzulegen ist, um den Zahlungsstrom des Investitionsprojekts zu replizieren, bzw. welcher Betrag im Zeitpunkt 0 maximal aufgenommen werden kann, wenn die Rückzahlung über den Zahlungsstrom des Investitionsprojekts erfolgen soll. Dieser Betrag wird als Barwert (oder Gegenwartswert) der zukünftigen Einzahlungsüberschüsse des Investitionsprojekts bezeichnet. Er wird ermittelt, indem die zukünftigen Überschüsse mit dem Zinssatz rf auf den Zeitpunkt 0 diskontiert werden:
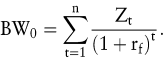
Der Barwert der Einzahlungsüberschüsse entspricht also dem Marktwert eines Portfolios bestehend aus risikofreien Anleihen, das einen mit dem Investitionsprojekt identischen Zahlungsstrom aufweist. Es gilt also das Prinzip der Wertadditivität, wonach der Wert der Summe mehrerer Zahlungsströme gleich der Summe der Werte der einzelnen Zahlungsströme ist.
Über die Vorteilhaftigkeit eines Investitionsprojekts lässt sich nun entscheiden, indem man den Barwert der zukünftigen Einzahlungsüberschüsse mit der Anschaffungsauszahlung (Preis) des Investitionsprojekts vergleicht. Übersteigt der Barwert die Anschaffungsauszahlung, so ist das Projekt vorteilhaft (Akzeptanzentscheidung), da es eine (risikofreie) Arbitragemöglichkeit eröffnet und seine Durchführung zu einer Steigerung des Vermögens der Eigentümer in Höhe der Differenz zwischen Barwert und Anschaffungsauszahlung führt. Diese Differenz wird als Kapitalwert des Investitionsprojekts bezeichnet: 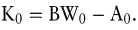
Existieren mehrere sich gegenseitig ausschließende Investitionsprojekte mit einem positiven Kapitalwert, soll dasjenige Projekt mit dem maximalen Kapitalwert gewählt werden (Auswahlentscheidung).
Bei der Ermittlung der Einzahlungsüberschüsse ist zu beachten, dass alle durch das Investitionsprojekt verursachten Zahlungen berücksichtigt werden, also auch diejenigen, die aufgrund des neuen Projekts bei bereits bestehenden Projekten anfallen. Synergieeffekte zwischen den bestehenden Investitionsprojekten und einem neu durchzuführenden Projekt sind also dem neuen Projekt zuzurechnen. Sofern Synergieeffekte zwischen Investitionsprojekten auftreten, die zeitgleich zur Auswahl stehen, so können diese nicht als eigenständige Investitionsprojekte interpretiert werden, über die isoliert zu urteilen ist. Vielmehr muss über Kombinationen von Investitionsprojekten (Investitionsprogramme) entschieden werden. Die alternativen Investitionsprogramme können dabei als sich gegenseitig ausschließende Investitionsprojekte interpretiert werden.
Es wurde davon ausgegangen, dass der risikofreie Zinssatz in jeder Periode gleich hoch ist, also eine flache Zinsstrukturkurve vorliegt. Ist dies nicht der Fall, so müssen für die unterschiedlichen Zeithorizonte die jeweiligen Kassazinssätze oder für jede einzelne Periode der entsprechende Terminzinssatz verwendet werden.
III. Methode des internen Zinsfußes
Ein alternatives Investitionsrechenverfahren ist die Methode des internen Zinsfußes. Der interne Zinsfuß i des Projekts ist derjenige Zinssatz, bei dem der Kapitalwert null ist:
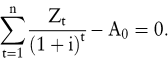
Der interne Zinsfuß wird auch als Rendite oder Effektivverzinsung bezeichnet. In der Praxis ist es populär, Investitionsprojekte anhand ihrer Renditen zu charakterisieren. Es scheint nahe liegend, folgende Entscheidungsregel heranzuziehen: Alle Projekte, deren interne Zinsfüße höher (niedriger) als der Kalkulationszinsfuß sind, sollten angenommen (abgelehnt) werden. Existieren mehrere Investitionsprojekte, deren interne Zinsfüße den Kalkulationszinssatz übersteigen und die sich gegenseitig ausschließen, so sollte dasjenige mit dem höchsten internen Zinsfuß gewählt werden.
Jedoch steht die Entscheidung auf der Basis von internen Zinsfüßen prinzipiell nur dann im Einklang mit dem Ziel der Maximierung des Kapitalwerts (des Vermögens), wenn sämtliche Projekte eine einperiodige Nutzungsdauer aufweisen und einander nicht ausschließen. Andernfalls können Probleme auftreten:
| - | Im Mehrperioden-Fall können Projekte existieren, die mehrere interne Zinsfüße aufweisen oder für die kein interner Zinsfuß existiert. Eine Anwendung des obigen Kriteriums ist dann nicht möglich. Zwar existiert bei so genannten Normalinvestitionen (deren Zahlungsreihe nur einen Vorzeichenwechsel aufweist) genau ein interner Zinsfuß. Probleme bei der Anwendung des obigen Kriteriums können dennoch auftreten, wenn die Zinsstrukturkurve nicht flach verläuft und nicht jeder mögliche Kalkulationszinsfuß unter dem internen Zinsfuß liegt: Mit welchem Kalkulationszinsfuß sollte dann der interne Zinsfuß verglichen werden? | | - | Außerdem gilt bei einander ausschließenden Projekten nicht, dass immer dasjenige Projekt vorteilhaft ist, das eine höhere Rendite erbringt. Das Projekt mit der höheren Rendite kann durchaus mit einem niedrigeren Kapitalwert und daher mit einem geringeren Vermögenszuwachs verbunden sein. | | - | Zudem gilt das Prinzip der Wertadditivität nicht. Die Vorteilhaftigkeitsbeurteilung sich gegenseitig ausschließender Investitionsprojekte kann sich ändern, wenn sie in Kombination mit anderen Projekten beurteilt werden. (Dies gilt selbst ohne Synergieeffekte und Finanzierungsrestriktionen.) |
Zwar kann die Methode des internen Zinsfußes in bestimmten Situationen derart modifiziert werden, dass eine Auswahl basierend auf dem internen Zinsfuß zu richtigen Entscheidungen im Sinne der Kapitalwertmethode führt. Diese Methoden sind jedoch nicht einfacher anzuwenden als die Kapitalwertmethode selbst. Die Shareholder-Value-Diskussion hat das Denken in Marktwerten derart gefördert, dass die Kapitalwertmethode auch in der Praxis zunehmende Verbreitung gefunden hat und deshalb der Versuch, die Methode des internen Zinsfußes zu „ retten “ , nicht notwendig zu sein scheint.
IV. Berücksichtigung von Unsicherheit und CAPM
Charakteristisch für Investitionsprojekte ist, dass zukünftige Einzahlungsüberschüsse im Zeitpunkt der Durchführung der Investition unsicher sind. Analog zum Vorgehen bei Sicherheit kann man riskante Zahlungsströme bewerten, indem ein Portfeuille bestehend aus Wertpapieren mit identischen Zahlungen in jedem möglichen zukünftigen Zeitpunkt und Umweltzustand gebildet wird. Kann ein solches Portfolio konstruiert werden, so führen Arbitrageargumente wieder dazu, dass der Wert des Investitionsprojekts dem Marktwert dieses Portfolios entspricht und zwar unabhängig von den Präferenzen der Eigentümer des Investitionsprojekts. (Auf diesem Bewertungsprinzip basiert beispielsweise die Bewertung von (Finanz-)Optionen und Terminkontrakten.)
In der Praxis ist es jedoch häufig schwierig (oder unmöglich), ein Portfolio zu konstruieren, das die Einzahlungsüberschüsse eines Investitionsprojekts repliziert. Modelle wie das Capital Asset Pricing Modell (CAPM) oder die Arbitrage Pricing Theorie zeigen Bedingungen auf, unter denen ein Projekt bewertet werden kann, ohne auf ein (völlig) identisches Portfolio zurückzugreifen. Die auch in der Praxis am weitesten verbreitete Methode ist das CAPM. Die Anwendung dieses Modells zur Bewertung von Investitionsprojekten wird zunächst für den Einperioden-Fall dargestellt. Bei Gültigkeit des CAPM sind zwei Charakteristika eines Investitionsprojekts bewertungsrelevant: der Erwartungswert und das Marktrisiko des zukünftigen Einzahlungsüberschusses. Bei der Anwendung der Kapitalwertmethode wird entsprechend die für den Fall sicherer Erwartungen dargestellte Formel zur Ermittlung des Barwerts modifiziert: Erstens tritt der Erwartungswert des unsicheren Einzahlungsüberschusses an die Stelle des sicheren Überschusses. Zweitens wird dem Marktrisiko Rechnung getragen. Hierzu gibt es zwei Möglichkeiten.
Bei der populäreren wird der Erwartungswert des Einzahlungsüberschusses mit einem risikoangepassten Zinssatz μ diskontiert. Dieser entspricht
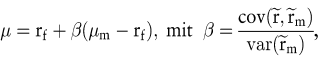
wobei μm die erwartete Rendite des Marktportfolios, 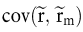 die Kovarianz der Rendite des Investitionsprojekts (bezogen auf dessen Barwert) mit der Rendite des Marktportfolios und die Kovarianz der Rendite des Investitionsprojekts (bezogen auf dessen Barwert) mit der Rendite des Marktportfolios und 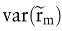 die Varianz der Rendite des Marktportfolios ist. β ist ein normiertes Maß für das bewertungsrelevante Risiko des Investitionsprojekts, das als Marktrisiko, systematisches Risiko oder Beta-Risiko des Investitionsprojekts bezeichnet wird. Soll β rechnerisch hergeleitet werden, so tritt das Problem auf, dass zur Berechnung der Kovarianz die Rendite des Investitionsprojekts bezogen auf dessen Barwert benötigt wird, der jedoch gerade ermittelt werden soll (Zirkularitätsproblem). In der Praxis wird β häufig aus historischen Daten von Projekten in gleichen Geschäftsfeldern ermittelt. Dieses Vorgehen unterstellt, dass β im Zeitablauf konstant ist; die Problematik dieser Annahme wird für den Mehrperioden-Fall noch angesprochen. die Varianz der Rendite des Marktportfolios ist. β ist ein normiertes Maß für das bewertungsrelevante Risiko des Investitionsprojekts, das als Marktrisiko, systematisches Risiko oder Beta-Risiko des Investitionsprojekts bezeichnet wird. Soll β rechnerisch hergeleitet werden, so tritt das Problem auf, dass zur Berechnung der Kovarianz die Rendite des Investitionsprojekts bezogen auf dessen Barwert benötigt wird, der jedoch gerade ermittelt werden soll (Zirkularitätsproblem). In der Praxis wird β häufig aus historischen Daten von Projekten in gleichen Geschäftsfeldern ermittelt. Dieses Vorgehen unterstellt, dass β im Zeitablauf konstant ist; die Problematik dieser Annahme wird für den Mehrperioden-Fall noch angesprochen.
Der Barwert der unsicheren Zahlung ergibt sich als
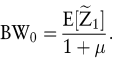
Alternativ kann das Risiko berücksichtigt werden, indem ein Risikoabschlag vom erwarteten Einzahlungsüberschuss vorgenommen wird und das resultierende Sicherheitsäquivalent mit dem risikolosen Zinssatz diskontiert wird. Das Sicherheitsäquivalent 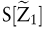 des Einzahlungsüberschusses beträgt des Einzahlungsüberschusses beträgt
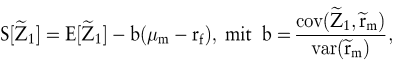
wobei 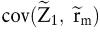 nun die Kovarianz der Einzahlung des Projekts mit der Rendite des Marktportfolios ist. Dies hat den Vorteil, dass bei der Ermittlung der Kovarianz das Zirkularitätsproblem nicht auftritt. Das Sicherheitsäquivalent ist diejenige sichere Zahlung, die auf dem Kapitalmarkt den gleichen Barwert aufweist, wie die unsichere Einzahlung des Investitionsprojekts. Daher wird das Sicherheitsäquivalent mit dem risikofreien Zinssatz diskontiert, um den Barwert zu erhalten: nun die Kovarianz der Einzahlung des Projekts mit der Rendite des Marktportfolios ist. Dies hat den Vorteil, dass bei der Ermittlung der Kovarianz das Zirkularitätsproblem nicht auftritt. Das Sicherheitsäquivalent ist diejenige sichere Zahlung, die auf dem Kapitalmarkt den gleichen Barwert aufweist, wie die unsichere Einzahlung des Investitionsprojekts. Daher wird das Sicherheitsäquivalent mit dem risikofreien Zinssatz diskontiert, um den Barwert zu erhalten:
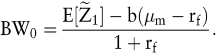
Richtig angewendet, führen beide Methoden zum gleichen Barwert, sodass die Auswahlentscheidung wie für den Fall sicherer Überschüsse entsprechend dem Kapitalwertkriterium erfolgen kann.
Das CAPM liefert für die Bewertung von Investitionsprojekten wichtige Einsichten:
| - | Aufgrund von Diversifikationseffekten auf dem Kapitalmarkt ist nicht die Streuung (Varianz) seines Einzahlungsüberschusses, sondern die Kovarianz (der Rendite) des Überschusses mit der Rendite des Marktportfolios bewertungsrelevant. Eine hohe Streuung des Überschusses ist daher noch keine Rechtfertigung für einen hohen Aufschlag auf den Zinssatz (bzw. ein niedriges Sicherheitsäquivalent). Ist der Überschuss nicht mit der Marktrendite korreliert, so gilt 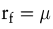 (bzw. (bzw. 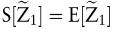 ), unabhängig von der Varianz des Überschusses. Ist die Korrelation negativ, so gilt ), unabhängig von der Varianz des Überschusses. Ist die Korrelation negativ, so gilt 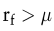 (bzw. (bzw.  ) und der Barwert des Überschusses steigt sogar mit steigender Varianz des Überschusses. ) und der Barwert des Überschusses steigt sogar mit steigender Varianz des Überschusses. | | - | Das (bewertungsrelevante) Risiko des Projekts und nicht das des Unternehmens beeinflusst den Wert eines Investitionsprojekts. Bei Anwendung eines risikoangepassten Zinssatzes darf der Kalkulationszinsfuß des Unternehmens daher nur dann verwendet werden, wenn beide (zufällig) das gleiche β-Risiko aufweisen. | | - | Es gilt wiederum das Prinzip der Wertadditivität. Hieraus folgt direkt, dass eine Diversifikation auf Unternehmensebene keinen eigenständigen Wert aufweist. |
Die Übertragung der Bewertungsidee des CAPM auf den Fall mehrerer Perioden erfolgt in der Praxis meist dadurch, dass ein einheitlicher risikoangepasster Kalkulationszinsfuß für alle Perioden verwendet wird:
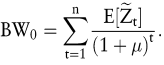
Diese Methode impliziert (für 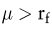 , dass das Sicherheitsäquivalent (der Risikoabschlag) eines konstanten erwarteten Überschusses im Zeitablauf in einer bestimmten Weise fällt (steigt). Somit ist sie nur für spezielle Risikostrukturen sinnvoll. Wenn beispielsweise der Überschuss des Projekts im Zeitpunkt t zwar stark mit der Marktrendite in der betreffenden Periode, nicht aber mit der Marktrendite in den vorangegangenen Perioden korreliert ist, dann führt dieses Verfahren zu einem zu hohen Risikoabschlag. Der risikoangepasste Kalkulationszinsfuß darf nur für die letzte Periode verwendet werden, während für die Perioden davor der risikofreie Zinssatz herangezogen werden sollte. Außerdem ist es für die Anwendung der Methode notwendig, dass das bewertungsrelevante Risiko, also β, selbst nicht stochastisch ist. (Zur Problematik der Übertragung des CAPM auf den Fall mehrerer Perioden vgl. z.B. Brealey, R./Myers, S. 2000; Copeland, T.E./Weston, J.F. 1988 sowie Grinblatt, M./Titman, S. 1998.) , dass das Sicherheitsäquivalent (der Risikoabschlag) eines konstanten erwarteten Überschusses im Zeitablauf in einer bestimmten Weise fällt (steigt). Somit ist sie nur für spezielle Risikostrukturen sinnvoll. Wenn beispielsweise der Überschuss des Projekts im Zeitpunkt t zwar stark mit der Marktrendite in der betreffenden Periode, nicht aber mit der Marktrendite in den vorangegangenen Perioden korreliert ist, dann führt dieses Verfahren zu einem zu hohen Risikoabschlag. Der risikoangepasste Kalkulationszinsfuß darf nur für die letzte Periode verwendet werden, während für die Perioden davor der risikofreie Zinssatz herangezogen werden sollte. Außerdem ist es für die Anwendung der Methode notwendig, dass das bewertungsrelevante Risiko, also β, selbst nicht stochastisch ist. (Zur Problematik der Übertragung des CAPM auf den Fall mehrerer Perioden vgl. z.B. Brealey, R./Myers, S. 2000; Copeland, T.E./Weston, J.F. 1988 sowie Grinblatt, M./Titman, S. 1998.)
Es ist empfehlenswert, grundsätzlich Sicherheitsäquivalente zu ermitteln und diese mit dem risikofreien Zinssatz zu diskontieren. Der Vorteil besteht erstens darin, dass die Gefahr eines pauschalen Risikoabschlags reduziert wird. Zweitens können zur Ermittlung von Sicherheitsäquivalenten häufig Marktinformationen herangezogen werden. Eine Anwendung des CAPM ist in diesen Fällen mitunter gar nicht notwendig. So entspricht beispielsweise der Futures Preis eines Rohstoffs dem Sicherheitsäquivalent seines Preises zum Laufzeitende des Futures-Kontrakts.
V. Berücksichtigung von Handlungsspielräumen und Realoptionen
Typischerweise lassen es Investitionsprojekte zu, flexibel auf zukünftige Umweltentwicklungen zu reagieren. Beispielsweise können Produktionsmengen der Nachfrage angepasst und Produktionsanlagen stillgelegt, erweitert oder zur Produktion neuer Produkte herangezogen werden. Solche Handlungsspielräume (strategische Optionen oder Realoptionen) können einen wesentlichen Einfluss auf den Wert eines Investitionsprojekts in einer Welt unsicherer Erwartungen haben und sind deshalb bei der Beurteilung von Investitionsalternativen zu berücksichtigen.
Die Methode, den Erwartungswert der Einzahlungsüberschüsse mit einem einheitlichen risikoangepassten Zinssatz zu diskontieren, kann hierfür jedoch nicht verwendet werden. Während der erwartete Einzahlungsüberschuss noch mit Hilfe eines Entscheidungsbaums (flexible Planung) ermittelt werden kann, ist die Berücksichtigung des immanenten Risikos problematisch. Die Existenz von Handlungsspielräumen führt im Mehrperioden-Fall dazu, dass das bewertungsrelevante Risiko der zukünftigen Einzahlungsüberschüsse im Zeitablauf stochastisch ist. Dies liegt daran, dass die optimale Ausübungsstrategie zustandsabhängig ist und die Verteilungsfunktion der Einzahlungsüberschüsse beeinflusst. Eine wichtige Voraussetzung für die Anwendung eines einheitlichen risikoangepassten Zinssatzes ist daher nicht erfüllt.
In der Literatur wird vorgeschlagen, Methoden der Bewertung von Finanzoptionen zur Bewertung von Handlungsspielräumen bei (Real-)Investitionsprojekten heranzuziehen. Black, F./ und Scholes, M. haben gezeigt, wie eine Aktienoption durch Bildung eines Portfolios bestehend aus den der Option zugrunde liegenden Aktien und risikofreien Anleihen repliziert werden kann. Auf einem arbitragefreien Markt muss der Wert der Aktienoption dem Marktwert des Portfolios entsprechen und zwar unabhängig von der Risikoeinstellung der Akteure. Basierend auf dieser Beobachtung kann das Sicherheitsäquivalent der möglichen Überschüsse zum Ausübungszeitpunkt der Option ermittelt werden. (Eine ausführliche Diskussion der Übertragung der Optionspreistheorie auf Realinvestitionsprojekte findet man z.B. in Brealey, R./Myers, S. 2000; Laux, C. 1993 und Trigeorgis, L. 1996.)
Ein wesentliches Element der Übertragung der Optionsbewertung auf die Bewertung von Realinvestitionen ist die Identifikation der wichtigsten Handlungsspielräume und des „ zugrunde liegenden Vermögensgegenstands “ (Underlying). Ein mögliches Problem einer direkten Übertragung der Optionsbewertung ist, dass für die Realoptionen zugrunde liegenden Vermögensgegenstände (wie z.B. das zu produzierende Gut) häufig keine Marktpreise existieren, die – wie der Aktienkurs – dem Barwert der möglichen Wertrealisation des Vermögensgegenstands zum Ausübungszeitpunkt der Option entsprechen. (Gegebenenfalls kann der Marktwert des Vermögensgegenstands unter Anwendung des CAPM ermittelt werden, da hierbei noch keine Handlungsspielräume auftreten und daher das Risiko nicht stochastisch ist.)
Neben der Problematik der Ermittlung des Werts des der Option zugrunde liegenden Vermögensgegenstands bei einem Investitionsprojekt gibt es einige weitere Aspekte, die die Bewertung eines Investitionsprojekts erschweren. Beispielsweise eröffnen Realinvestitionsprojekte häufig vielfältige interdependente Handlungsspielräume (z.B. erwirbt man mit der Ausübung der Option, eine Produktionsanlage zu kaufen, die Option zu produzieren), der „ Ausübungskurs “ (z.B. die Kosten der Produktion) kann ebenfalls unsicher sein, und analog einer Aktie, die während der Optionslaufzeit Dividenden ausschüttet, ist die Verfügung über den der Option zugrunde liegenden Vermögensgegenstand häufig mit Vorteilen (convenience yield oder Objektertrag) verbunden (z.B. Erträge einer Produktionsanlage). Die Theorie zur Bewertung von Finanzoptionen liefert Verfahren zur Berücksichtigung dieser Aspekte. Darüber hinaus vermittelt die Optionspreistheorie Einsichten, die auch für Realinvestitionsprojekte interessant sind, und zwar insbesondere auch deshalb, weil sie die Problematik einfacher Investitionsrechenverfahren deutlich machen:
| - | Eine Option auf eine Aktie wird nicht sofort ausgeübt, wenn der Aktienpreis über dem Basiskurs liegt. Entsprechend ist es auch nicht vorteilhaft, jede Realinvestition mit einem positiven Kapitalwert sofort auszuüben. Die Option auf eine Investition kann einen höheren Wert aufweisen als die Investition selbst. Entgehen durch Aufschieben einer Investition keine Erträge, so wird die Investition erst zum spätest möglichen Zeitpunkt durchgeführt. | | - | Die Wahrscheinlichkeit einer frühzeitigen Investition ist umso höher, je höher die Objektertäge sind, die durch ein Aufschieben der Option verloren gehen. | | - | Der Wert einer Option ist umso größer, je höher ceteris paribus die Varianz der möglichen Werte des der Option zugrunde liegenden Vermögensgegenstands ist. Unsicherheit kann sich also positiv auf den Wert eines Investitionsprojekts auswirken. | | - | Der Wert einer Investitionsmöglichkeit kann sich erhöhen, wenn der risikofreie Zins steigt und der Investitionshorizont größer wird. Das traditionelle Argument, dass der Barwert eines Zahlungsstroms sinkt, wenn die Zahlung zu einem späteren Zeitpunkt erfolgt und der risikofreie Zins steigt, kann daher nicht ohne weiteres auf den Barwert von Handlungsspielräumen übertragen werden. |
Literatur:
Brealey, Richard/Myers, Stewart : Principles of Corporate Finance, Boston, 6. A., 2000
Copeland, Thomas E./Weston, J. Fred : Financial Theory and Corporate Policy, Reading et al., 3. A., 1988
Franke, Günter/Hax, Herbert : Finanzwirtschaft des Unternehmens und Kapitalmarkt, Berlin et al., 4. A., 1999
Grinblatt, Mark/Titman, Sheridan : Financial Markets and Corporate Strategy, Boston et al. 1998
Hax, Herbert : Investitionstheorie, Würzburg, 5. A., 1985
Kruschwitz, Lutz : Investitionsrechnung, München et al., 8. A., 2000
Kruschwitz, Lutz : Finanzierung und Investition, München et al., 2. A., 1999
Laux, Christian : Handlungsspielräume im Leistungsbereich des Unternehmens: Eine Anwendung der Optionspreistheorie, in: ZfbF, Jg. 45, 1993, S. 933 – 958
Laux, Helmut : Risikoteilung, Anreiz und Kapitalmarkt, Berlin et al. 1998
Laux, Helmut : Flexible Investitionsplanung, Opladen 1971
Schmidt, Reinhard H./Terberger, Eva : Grundzüge der Investitions- und Finanzierungstheorie, Wiesbaden, 4. A., 1997
Trigeorgis, Lenos : Real Options: Managerial Flexibility and Strategy in Resource Allocation, Cambridge et al. 1996
Trigeorgis, Lenos : Real Options in Capital Investment: Models, Strategies and Applications, Westport et al. 1995
|