|
Optimierungs- und Simulationsmodelle
Inhaltsübersicht
I. Optimierungsmodelle
II. Simulationsmodelle
I. Optimierungsmodelle
1. Definition
Modelle sind vereinfachte Abbildungen der Realität. Erklärungsmodelle zeigen bestimmte Aspekte der Realität auf. Entscheidungsmodelle dienen der Entscheidungsvorbereitung, indem sie aus einer vorgegebenen Menge von Alternativen diejenigen auswählen, die einer vorgegebenen Zielsetzung am besten entsprechen. Ein Spezialfall von Entscheidungsmodellen sind Optimierungsmodelle, die die folgende Struktur aufweisen (vgl. Kistner, K.-P. 1993, S. 1 f.):
Gegeben sind Entscheidungsalternativen, die durch Zahlen bzw. Vektoren charakterisiert werden können:
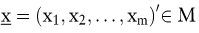
wobei M die Menge der zulässigen Entscheidungen ist. Weiter sei
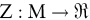
die Zielfunktion 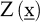 sei eine Abbildung der Menge der zulässigen Entscheidungen in die Menge der reellen Zahlen, die anzeigt, wie wünschenswert eine Entscheidung sei eine Abbildung der Menge der zulässigen Entscheidungen in die Menge der reellen Zahlen, die anzeigt, wie wünschenswert eine Entscheidung 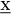 ist. ist.
Weiter seien die Restriktionen 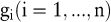 Abbildungen des Abbildungen des 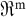 in die Menge der reellen Zahlen in die Menge der reellen Zahlen 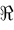 . Berücksichtigt man, dass die Entscheidungsvariablen nur nicht-negative Werte annehmen können, dann hat ein Optimierungsmodell die Form: . Berücksichtigt man, dass die Entscheidungsvariablen nur nicht-negative Werte annehmen können, dann hat ein Optimierungsmodell die Form:
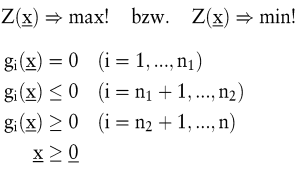
Sind die Zielfunktion und die Restriktionen linear, dann liegt ein lineares Programm vor (zur linearen Optimierung vgl. z.B. Dantzig, G.B./Thapa, M.N. 1997; Gal, T. 1973; Gass, S.I. 1985; Hadley, G. 1962; Kistner, K.-P. 1993). In konvexen Programmen sind die zu minimierende Zielfunktion sowie alle Restriktionen konvex und vom Typ „ kleiner oder gleich “ . Ein Optimierungsproblem ist auch dann konvex, wenn diese Eigenschaften durch Multiplikation von Zielfunktion oder Restriktionen mit – 1 erreicht werden kann (zur konvexen Programmierung vgl. Horst, R. 1991; Kistner, K.-P. 1993; Künzi, H.-P./Krelle, W./v. Randow, R. 1979). Dürfen alle Variablen nur ganzzahlige Werte annehmen, dann spricht man von einem rein ganzzahligen Optimierungsproblem; gilt diese Bedingung nur für einige Variablen, dann liegt ein gemischt-ganzzahliges Problem vor. Ein Spezialfall ganzzahliger Optimierungsmodelle sind binäre Programme, bei denen einige Variablen nur die Werte 0 oder 1 annehmen können. (Zur ganzzahligen Optimierung vgl. Burkard, R.E. 1992).
Die Theorie der Optimierungsmethoden befasst sich mit Bedingungen, denen optimale Lösungen dieser Probleme genügen, und mit Verfahren zu deren Bestimmung. Auch wenn es deren Zielsetzung suggeriert, können Optimierungsmodelle niemals optimale Entscheidungen determinieren; sie liefern lediglich Entscheidungsvorschläge, die durch den Entscheidenden selbstverständlich modifiziert werden können. Insbesondere sind bei der endgültigen Entscheidung qualitative oder andere Gesichtspunkte zu berücksichtigen, die in dem Optimierungsmodell nicht berücksichtigt werden können.
2. Lineare Optimierung a) Definition
Ein lineares Optimierungsmodell hat die Form
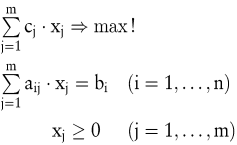
Durch Einführung nicht-negativer Schlupfvariablen und die Multiplikation mit – 1 kann jedes lineare Optimierungsproblem auf diese Standardform gebracht werden.
Zur Lösung derartiger Programme stehen effiziente Lösungsverfahren zur Verfügung. Diese beruhen auf zwei Grundansätzen:
| - | Das Simplex-Verfahren von G. B. Dantzig, 1963 macht davon Gebrauch, dass optimale Lösungen entweder in einem Eckpunkt des durch die Restriktionen aufgespannten Polyeders liegen oder als Konvexkombination optimaler Eckpunkte dargestellt werden können. Das Verfahren sucht daher systematisch die Ecken dieses Polyeders ab und findet in einer endlichen Zahl von Schritten eine optimale Lösung, falls eine solche existiert (Dantzig, G.B. 1963). | | - | Eine neuerer Lösungsansatz, der das Innere der Menge der zulässigen Lösungen absucht, geht auf Khachian (Khachian, L. 1979) zurück und wurde von Karmarkar (Karmarkar, N.K. 1984) zu einem auch für praktische Zwecke einsetzbaren Algorithmus ausgebaut. |
Es existieren Computerprogramme, die auch große lineare Optimierungsprobleme effizient lösen. b) Eigenschaften der Lösung linearer Optimierungsprobleme
Falls eine optimale Lösung eines linearen Optimierungsproblems existiert, dann gibt es auch immer eine optimale Lösung, bei der die Zahl der von Null verschiedenen Variablen höchstens gleich der Zahl der Restriktionen ist. Existieren mehrere solcher Lösungen, dann ist auch jede Konvexkombination optimal.
Zu jedem linearen Programm lässt sich ein duales Problem angeben. Im Fall eines speziellen Maximum-Problems
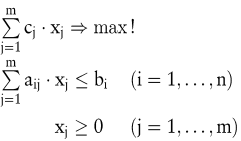
hat das Dual die Form:
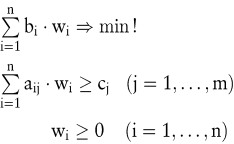
Zwischen dem ursprünglichen Problem, dem Primal, und dem Dual bestehen folgende Beziehungen:
| - | Das Dual des Duals ist das Primal. | | - | Der Zielfunktionswert jeder zulässigen Lösung des Primals ist kleiner oder gleich dem Zielfunktionswert jeder zulässigen Lösung des Duals. | | - | Ist der Zielfunktionswert einer zulässigen Lösung des Primals gleich dem Zielfunktionswert einer zulässigen Lösung des Duals, dann sind beide Lösungen optimal. | | - | Das Simplex-Verfahren zur Lösung linearer Optimierungsprobleme liefert neben einer optimalen Lösung des Primals auch die optimale Lösung des Duals. | | - | Zwischen einer optimalen Lösung  des Primals und einer entsprechenden optimalen Lösung des Duals des Primals und einer entsprechenden optimalen Lösung des Duals 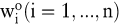 besteht folgende Beziehung (Preistheorem): besteht folgende Beziehung (Preistheorem): |
Falls 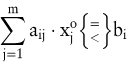 dann ist dann ist 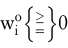
für alle 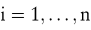
Falls 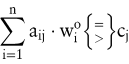 dann ist dann ist 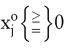
für alle 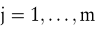
| - | Die Dualvariablen können als Bewertungen der Restriktionen angesehen werden. Sie geben die relative Änderung des Zielfunktionswerts der optimalen Lösung in Bezug auf eine Veränderung der entsprechenden Restriktionskonstanten an, soweit dadurch kein Basiswechsel erzwungen wird. Mit dieser Interpretation der Dualvariablen als Schattenpreise lässt sich das Preistheorem wie folgt lesen: Eine Dualvariable 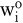 kann nur dann positiv sein, wenn die entsprechende Restriktion ausgeschöpft ist. Ist eine Beschränkung nicht bindend, dann ist die Dualvariable gleich Null. Weiter ist eine Problemvariable kann nur dann positiv sein, wenn die entsprechende Restriktion ausgeschöpft ist. Ist eine Beschränkung nicht bindend, dann ist die Dualvariable gleich Null. Weiter ist eine Problemvariable 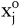 nur dann positiv, wenn die mit Schattenpreisen bewertete Inanspruchnahme der Restriktion durch eine Einheit der Variablen gleich dem Zielfunktionsbeitrag nur dann positiv, wenn die mit Schattenpreisen bewertete Inanspruchnahme der Restriktion durch eine Einheit der Variablen gleich dem Zielfunktionsbeitrag 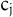 ist. Ist die bewertete Inanspruchnahme der Restriktion größer als der Zielfunktionsbeitrag, dann ist die Problemvariable gleich Null. ist. Ist die bewertete Inanspruchnahme der Restriktion größer als der Zielfunktionsbeitrag, dann ist die Problemvariable gleich Null. | | - | Die Dualitätstheorie ist auch auf allgemeine lineare Optimierungsprobleme übertragbar. Dabei ist allerdings zu beachten, dass die zu Restriktionen der Form „ größer oder gleich “ gehörenden Dualvariablen negativ sind und die den Beschränkungen in Gleichungsform zugeordneten Schattenpreise nicht im Vorzeichen beschränkt sind. |
Bei der Begründung von Entscheidungen ist man nicht nur an der optimalen Lösung eines Optimierungsproblems interessiert. Vielmehr möchte man auch wissen, wie diese auf Änderungen der Daten und auf Abweichungen von der Empfehlung reagiert. Mit dieser Frage befassen sich Sensitivitätsanalyse und parametrische Programmierung (vgl. hierzu: Dinkelbach, W. 1969; Gal, T. 1973).
Die Sensitivitätsanalyse untersucht, in wie weit ein Datum eines linearen Optimierungsproblems – insbesondere ein Koeffizient der Zielfunktion oder eine Beschränkungskonstante, aber auch ein Koeffizient der Beschränkungsmatrix – verändert werden kann, ohne dass dadurch die Struktur der Lösung und damit der optimale Wert der Dualvariablen verändert wird.
Angenommen, die Zielfunktionskoeffizienten oder die Restriktionskonstanten seien lineare Funktionen eines Parameters t:
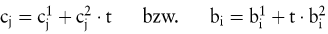
Die parametrische lineare Programmierung untersucht, wie die optimale Lösung und der optimale Zielfunktionswert eines linearen Optimierungsproblems auf eine systematische Variation des Parameters t reagieren. Dabei gilt Folgendes:
| - | Der Parameter t kann innerhalb eines abgeschlossenen Intervalls variiert werden. | | - | Innerhalb dieses Intervalls gibt es eine endliche Zahl von kritischen Punkten, in denen ein Basiswechsel stattfindet. | | - | Zwischen zwei benachbarten kritischen Punkten bleiben die optimalen Werte der Dualvariablen konstant, in den kritischen Punkten ändern sie sich abrupt. | | - | Die Zielfunktion in Abhängigkeit von dem Parameter t ist eine stückweise lineare Funktion mit einer endlichen Zahl von Knicken in den kritischen Punkten. In einem Minimum-Problem ist diese Funktion konvex, in einem Maximum-Problem ist sie konkav. Sind in einem Maximum-Problem alle Restriktionen in der Form „ kleiner oder gleich “ gegeben, dann ist diese Funktion monoton steigend. In einem Minimum-Problem, in dem alle Restriktionen in der Form „ größer oder gleich “ gegeben sind, ist diese Funktion monoton fallend. Andernfalls ist sie unimodal. | c) Anwendungen der linearen Optimierung in der Unternehmensplanung und in der Unternehmensrechnung
Schon früh wurde erkannt, dass lineare Optimierungsmodelle zur Erzeugung von Entscheidungsvorschlägen in der betrieblichen Planung einsetzbar sind. In der Produktions-Programmplanung sind die Zielfunktionskoeffizienten eines linearen Optimierungsmodells 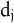 als Deckungsbeiträge von Produkten, die Beschränkungskonstanten als Deckungsbeiträge von Produkten, die Beschränkungskonstanten 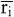 als Kapazitäten von Maschinen und der Bereitstellung anderer Produktionsfaktoren anzusehen. Die Koeffizienten der Beschränkungsmatrix als Kapazitäten von Maschinen und der Bereitstellung anderer Produktionsfaktoren anzusehen. Die Koeffizienten der Beschränkungsmatrix 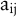 können als Produktionskoeffizienten interpretiert werden. Führt man Beschränkungen der Absatzmengen der Produkte können als Produktionskoeffizienten interpretiert werden. Führt man Beschränkungen der Absatzmengen der Produkte 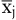 ein, dann erhält man als Grundmodell der Produktionsplanung (vgl. z.B. Kistner, K.-P./Steven, M. 2001, S. 192 – 194): ein, dann erhält man als Grundmodell der Produktionsplanung (vgl. z.B. Kistner, K.-P./Steven, M. 2001, S. 192 – 194):
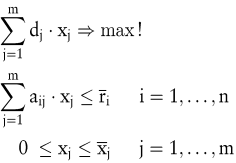
Auf der Grundlage dieses Grundmodells entwickeln Böhm/Wille (Böhm, H.-H./Wille, F. 1974) ein System zur Bewertung des Einsatzes knapper Kapazitäten mit Opportunitätskosten und die Grenzerfolgskalkulation. Bezeichnet man mit 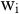 die den Kapazitäten zugeordneten Dualvariablen, dann sind die Opportunitätskosten der Nutzung der Kapazitäten: die den Kapazitäten zugeordneten Dualvariablen, dann sind die Opportunitätskosten der Nutzung der Kapazitäten:
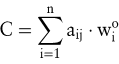
Das Kalkulationsschema der Grenzerfolgskalkulation ist gegeben durch:

Wegen der Beschränkung des Absatzes ergibt sich aus dem Preistheorem:
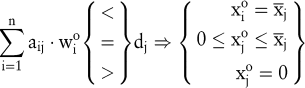
Ist die mit Opportunitätskosten bewertete Kapazitätsnutzung durch eine Produkteinheit kleiner als ihr Deckungsbeitrag, dann ist die optimale Produktionsmenge gleich dem maximal möglichen Absatz; sind diese Kosten größer als der Deckungsbeitrag, dann lohnt es sich nicht, das Produkt zu produzieren; sind sie gleich dem Deckungsbeitrag, dann ist die optimale Ausbringungsmenge nicht bestimmt; sie liegt zwischen Null und der Absatzgrenze.
Gegen die Grenzerfolgskalkulation wird eingewandt, dass Opportunitätskosten erst bekannt sind, wenn das optimale Produktionsprogramm bestimmt ist. Sie ermöglicht jedoch die Beurteilung von Datenänderungen und Abweichungen von einem mit Hilfe der linearen Optimierung bestimmten Produktionsplan. Zu verweisen ist insbesondere auf die Kalkulation von Zusatzaufträgen.
Ein weiteres Anwendungsgebiet ist die Investitionsplanung (vgl. z.B. Albach, H. 1962; Weingartner, M.H. 1963; Hax, H. 1964). In diesen Ansätzen sind die Zielfunktionskoeffizienten Kapitalwerte von Investitionsobjekten oder deren Endwerte; die Restriktionen sind als Bilanzgleichungen zu interpretieren, die sicherstellen, dass das finanzielle Gleichgewicht eingehalten wird.
Die Dualvariablen, die den Bedingungen für das finanzielle Gleichgewicht zugeordnet sind, sind gleich den Opportunitätskosten für die Inanspruchnahme von Kapital in einer Periode. Soll der Endwert des Vermögens maximiert werden, dann geben diese die Reaktion des Endwerts auf eine Veränderung der Kapitalaufnahme in einer Periode an. Aus diesen Größen können interne Kalkulationszinsfüße hergeleitet werden, indem man sie durch die Opportunitätskosten für die Kapitalaufnahme in der Anfangsperiode dividiert (Franke, G./Laux, H. 1968). Bewertet man die Zahlungsströme in den einzelnen Perioden mit diesen endogenen Zinsfüßen und bestimmt so einen Kapitalwert, dann kann man mit dem Kapitalwertkriterium eine optimale Investitionspolitik bestimmen, ohne die Restriktionen des Modells explizit zu berücksichtigen. Gegen diesen Vorschlag ist einzuwenden, dass die endogenen Kalkulationszinsfüße erst bekannt sind, wenn ein optimaler Investitionsplan vorliegt. Man kann das Verfahren aber dazu nutzen, Abweichungen von dem optimalen Investitionsplan, insbesondere die Aufnahme neuer Investitionsobjekte, zu beurteilen.
3. Ganzzahlige lineare Optimierung
In einem ganzzahligen Optimierungsproblem dürfen alle oder einige Variablen nur ganzzahlige Werte annehmen. Natürliche Ganzzahligkeitsbedingungen sind darauf zurückzuführen, dass bestimmte Entscheidungsalternativen nur mit ganzzahligen Werten realisierbar sind. Daneben können sich Ganzzahligkeiten auch aus logischen Bedingungen ergeben, denen die Lösung eines Optimierungsmodells genügen muss: In der Produktionsplanung sind Rüstkosten zu berücksichtigen, die nur dann anfallen, wenn eine positive Menge erzeugt wird (vgl. z.B. Kistner, K.-P. 1993, S. 150). In der Reihenfolgenplanung kann immer nur eines von zwei Objekten vor dem anderen eingeplant werden (vgl. Manne, A.S. 1960; Kistner, K.-P. 1993, S. 149). In beiden Fällen kann man mithilfe von binären Variablen Nebenbedingungen formulieren, die sicherstellen, dass die entsprechenden Bedingungen eingehalten werden.
Viele Planungsprobleme lassen sich als gemischt-ganzzahlige Optimierungsmodelle formulieren. Im Gegensatz zu stetigen Problemen ist es nicht möglich, beliebig große diskrete Modelle mit angemessenem Rechenaufwand zu lösen. Die Komplexitätstheorie hat gezeigt, dass gerade die meisten in der Praxis auftretenden Reihenfolgen-Probleme schwer sind, d.h. es gibt keinen Algorithmus, für den der Rechenaufwand durch ein Polynom in der Problemgröße beschränkt werden kann (vgl. z.B. Brüggemann, W. 1995). Zur Lösung solcher Probleme ist der Einsatz von Heuristiken erforderlich. Neben einfachen Heuristiken, die Problemlösungen mit Hilfe von Prioritätsregeln aufbauen, werden Meta-Heuristiken und naturanaloge Verfahren empfohlen (vgl. Feldmann, M. 1999).
4. Konvexe Optimierung
In einem konvexen Programm in der Standardform:
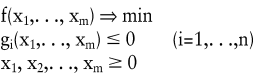
sind die Funktionen f und gi konvex. Sind sie außerdem stetig und differenzierbar, dann lassen sich lokale Optimalitätsbedingungen, die Kuhn-Tucker-Bedingungen, herleiten (Kuhn, H.W./Tucker, A.W. 1950; Künzi, H.P./Krelle, W./v. Randow, R. 1979, S. 55 ff.). Hierzu bildet man die Lagrange-Funktion, indem man zur Zielfunktion die gewichtete Summe der Restriktionen addiert:
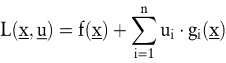
Falls das konvexe Optimierungsproblem eine innere Lösung 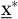 besitzt, dann ist besitzt, dann ist 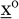 genau dann eine optimale Lösung, wenn es ein genau dann eine optimale Lösung, wenn es ein 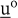 gibt, sodass gibt, sodass
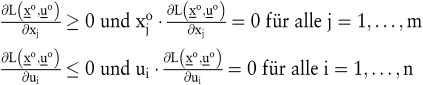
Die Lagrange-Multiplikatoren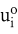 können als Schattenpreise interpretiert werden, die angeben, wie der Zielfunktionswert der optimalen Lösung auf eine Veränderung der Restriktionskonstanten reagiert. Das Preistheorem der linearen Programmierung ist ein Spezialfall der Kuhn-Tucker-Bedingungen. können als Schattenpreise interpretiert werden, die angeben, wie der Zielfunktionswert der optimalen Lösung auf eine Veränderung der Restriktionskonstanten reagiert. Das Preistheorem der linearen Programmierung ist ein Spezialfall der Kuhn-Tucker-Bedingungen.
Ein wichtiger Spezialfall der konvexen Optimierung ist die quadratische Programmierung, bei der eine definite oder semi-definite quadratische Zielfunktion unter linearen Nebenbedingungen zu minimieren ist:
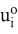
Ein Anwendungsfall ist die Bestimmung eines optimalen Wertpapier-Portefeuilles (vgl. Markowitz, H.M. 1969): In einem quadratischen Optimierungsmodell wird die Varianz der Rendite eines Portefeuilles unter der Nebenbedingung minimiert, dass deren Erwartungswert einen Mindestwert nicht unterschreitet. Um die Effizienzlinie, die Menge der bezüglich Erwartungswert und Varianz der Rendite effizienten Portefeuilles zu bestimmen, wird diese Mindestrendite parametrisch variiert.
5. Dynamische Optimierung
Dynamische Optimierungsmodelle unterscheiden sich von anderen Optimierungsproblemen dadurch, dass sie eine sequentielle, insbesondere eine zeitliche Struktur aufweisen.
Das Grundmodell hat die folgende Form (vgl. z.B. Kistner, K.-P. 1993, S. 6; Schneeweiß, C. 1974, S. 20):
Es sei 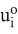 der Zustand des Systems in den Zeitpunkten der Zustand des Systems in den Zeitpunkten 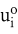 und und 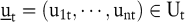 der Vektor der Kontrollvariablen, die es ermöglichen, den Systemzustand autonom zu beeinflussen. Ut ist die Menge der möglichen Werte der Kontrollvariablen der Vektor der Kontrollvariablen, die es ermöglichen, den Systemzustand autonom zu beeinflussen. Ut ist die Menge der möglichen Werte der Kontrollvariablen 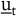 . Dann ist die Systemdynamik gegeben durch: . Dann ist die Systemdynamik gegeben durch:
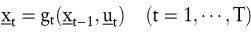
Für t = 0 sind Anfangswerte 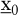 , für t = T sind meist Endwerte vorgegeben , für t = T sind meist Endwerte vorgegeben 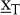 . Die Funktionen gt heißen Systemdynamik. . Die Funktionen gt heißen Systemdynamik.
Die dynamische Optimierung versucht, die Kontrollvariablen 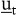 so zu bestimmen, dass eine vorgegebene Zielfunktion so zu bestimmen, dass eine vorgegebene Zielfunktion
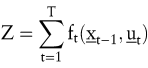
maximiert oder minimiert wird.
Grundlegend für die Lösung dynamischer Programme ist das Optimalitätsprinzip von Bellman, (vgl. Bellman, R.E. 1957, S. 10; Beckmann, M.J. 1968): Ein dynamisches Optimierungsproblem kann in zwei Teilprobleme zerlegt werden, die Entscheidung in der ersten Periode und die Entscheidungen in den folgenden Perioden. Daraus ergibt sich die Bellman-Gleichung:
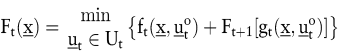
Dabei sind 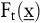 die Kosten der optimalen Entscheidung in den Perioden die Kosten der optimalen Entscheidung in den Perioden 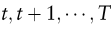 unter der Voraussetzung, dass sich das System zu Beginn der Periode im Zustand unter der Voraussetzung, dass sich das System zu Beginn der Periode im Zustand 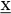 befindet. befindet.
Die Lösung dieser Rekursionsgleichung erfolgt mit Hilfe der optimalen Rückkopplungssteuerung (vgl. Kistner, K.-P. 1993, S. 202; Neumann, K./Morlock, M. 1993, S. 602): In der Rückwärtsrekursion wird, beginnend mit der letzten Periode, eine Folge von Politiken – bedingten Entscheidungen – 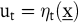 bestimmt, die für jeden Ausgangszustand bestimmt, die für jeden Ausgangszustand 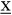 angeben, welche Entscheidung angeben, welche Entscheidung 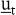 in der Periode t zu treffen ist. In der Vorwärtsrekursion wird dann – ausgehend von dem Ausgangszustand – die Folge der tatsächlich zu treffenden optimalen in der Periode t zu treffen ist. In der Vorwärtsrekursion wird dann – ausgehend von dem Ausgangszustand – die Folge der tatsächlich zu treffenden optimalen 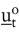 Entscheidungen ermittelt. Entscheidungen ermittelt.
Die dynamische Programmierung wird z.B. in der Lagerhaltungstheorie zur Bestimmung der optimalen Losgröße bei schwankender Nachfrage benutzt (vgl. z.B. Wagner, H.M./Whitin, T.M. 1958/59;Arrow, K.J./Harris, T./Marschak, J. 1951). Sie ist jedoch nicht auf die Bestimmung optimaler Entscheidungen im Zeitablauf beschränkt, sie kann auch zur Lösung sequentiell strukturierter Probleme wie die Bestimmung optimaler Wege durch ein Netzwerk (vgl. z.B. Dreyfus, S.E./Law, A.M. 1977, S. 50 – 68) eingesetzt werden.
II. Simulationsmodelle
Unter Simulation kann man mathematische Experimente verstehen, die statistische Aussagen über Eigenschaften von Modellen ermöglichen, für die keine mathematisch exakten Lösungen ermittelt werden können. Sie sind erforderlich, weil die zu untersuchenden Sachverhalte vielfach zu komplex sind, um sie in einem exakten Optimierungsmodell abzubilden und einer Lösung zuzuführen (zur Simulation vgl. Bratley, P./Fox, B.L./Schrage, L.E. 1987; Law, A.M./Kelton, D.W. 1991).
1. Simulation stochastischer Prozesse
Stochastische Prozesse kann man als dynamische Modelle auffassen, die durch zufällige Einwirkungen beeinflusst werden. Bei deren Simulation wird zunächst ein Modell entwickelt, das das Verhalten des zu untersuchenden Systems beschreibt. Es werden die Zustände, die dieses System annehmen kann, die Ereignisarten, die den Systemzustand verändern, und die Beziehungen zwischen diesen und den Zuständen erfasst. Weiter wird ein Ausgangszustand festgelegt, in dem sich das System bei Beginn des Simulationslaufs befindet. Das Verfahren geht wie folgt vor:
Als erstes wird für jede Ereignisart der Zeitpunkt des nächsten Eintritts bestimmt. Hierzu wird mit Hilfe eines Zufallszahlengenerators eine Realisation einer Zufallsvariablen generiert, die der Verteilung der Abstände der Ereignisse entspricht, und damit der Termin des nächsten Eintritts festgelegt. Aus der Menge der Termine für die einzelnen Ereignisarten wird das Minimum ermittelt und so das als nächstes auftretende Ereignis terminiert. Dann werden die durch dieses Ereignis ausgelösten Änderungen des Systemzustandes bestimmt sowie der Termin für das nächste Eintreten der betreffenden Ereignisart mittels einer entsprechenden Zufallszahl ermittelt. Dieses Vorgehen wird wiederholt, bis ein vorgegebenes Abbruchkriterium erfüllt ist; so erhält man eine Realisation des durch das Modell beschriebenen stochastischen Prozesses.
Erzeugt man mehrere Simulationsläufe, dann erhält man eine Stichprobe dieses Prozesses, aus der statistische Kenngrößen zu seiner Charakterisierung zu bestimmen sind.
Derartige Simulationen werden insbesondere in der Produktionsplanung eingesetzt. Es sind Programmpakete wie z.B. ARENA oder GPSS verfügbar, die die Formulierung von Simulationsmodellen und deren Durchführung unterstützen.
2. What-If-Analysen
Bei weiter Fassung des Begriffs kann man unter Simulationsmodellen auch What-If-Analysen verstehen. Diese verändert in Entscheidungsmodellen Parameterwerte und Entscheidungsvariablen systematisch oder zufällig, um einen Eindruck von der Reaktion einer vorgegebenen Zielfunktion auf diese Änderungen zu erhalten. Mit der What-If-Analyse kann man insbesondere überprüfen, welche Auswirkungen bestimmte Entscheidungen auf den Zielfunktionswert haben. Das Verfahren wird u.a. durch Spread-Sheet-Programme wie Excel, Lotus 1-2-3 oder Quattro unterstützt.
3. Naturanaloge Verfahren
Schließlich kann man auch die oben angeführten naturanalogen Verfahren zu Lösung komplexer Optimierungsprobleme als Spezialfall von Simulationsmodellen ansehen: Hier werden bestimmte Lösungsheuristiken mit Hilfe der Simulation von Optimierungsprozessen der Natur nachempfunden.
Literatur:
Albach, Horst : Investition und Liquidität, Wiesbaden 1962
Arrow, Kenneth J./Harris, Theodore/Marschak, Jakob : Optimal Inventory Policy, in: Econometrica, Jg. 19, 1951, S. 250 – 272
Beckmann, Martin J. : Dynamic Programming of Economic Decisions, Berlin et al. 1968
Bellman, Richard E. : Dynamic Programming, Princeton 1957
Böhm, Hans-Hermann/Wille, Friedrich : Deckungsbeitragsrechnung, Grenzpreisrechnung und Optimierung, München, 5. A., 1974
Bratley, Paul/Fox, Bennet L./Schrage, Linus E. : A Guide to Simulation, Berlin et al., 2. A., 1987
Brüggemann, Wolfgang : Ausgewählte Probleme der Produktionsplanung. Komplexität und neuere Lösungsmöglichkeiten, Heidelberg 1995
Burkard, Rainer E. : Ganzzahlige Optimierung, in: Grundlagen des Operations Research Bd. 2, hrsg. v. Gal, Tomas, Berlin et al., 3. A., 1992, S. 361 – 502
Dantzig, George B. : Linear Programming and Extensions, Princeton 1963
Dantzig, Geoge B./Thapa, Mukund N. : Linear Programming 1: Introduction, New York et al. 1997
Dinkelbach, Werner : Sensitivitätsanalysen und parametrische lineare Programmierung, Berlin et al. 1969
Dreyfus, Stuart E./Law, Averill M. : The Art and Theory of Dynamic Programming, New York et al. 1977
Feldmann, Martin : Naturanaloge Verfahren. Metaheuristiken zur Reihenfolgenplanung, Wiesbaden 1999
Franke, Günter/Laux, Helmut : Die Ermittlung der Kalkulationszinsfüße für investitionstheoretische Partialmodelle, in: ZfbF, Jg. 20, 1968, S. 740 – 759
Gal, Tomas : Lineare Optimierung, in: Grundlagen des Operations Research Bd. 1, hrsg. v. Gal, Tomas, Berlin et al., 3. A., 1991, S. 56 – 224
Gal, Tomas : Betriebliche Entscheidungsprobleme, Sensitivitätsanalyse und parametrische Programmierung, Berlin et al. 1973
Gass, Saul I. : Linear Programming – Methods and Application, New York, 5. A., 1985
Hadley, George : Linear Programming, Reading/Mass. 1962
Hax, Herbert : Investitionsplanung mit Hilfe der linearen Programmierung, in: ZfbF, 1964, Bd. NF 16, S. 430 – 446
Horst, Reiner : Nichtlineare Optimierung, in: Grundlagen des Operations Research Bd. 1, hrsg. v. Gal, Tomas, Berlin et al., 3. A., 1991, S. 255 – 419
Karmarkar, Narendra K. : A New Polynomial-Time Algorithm for Linear Programming, in: Combinatorica, Jg. 4, 1984, S. 373 – 395
Khachian, L. : A Polynomial Algorithm in Linear Programming, in: Soviet Mathematics Doklady, Jg. 20, 1979, S. 191 – 194
Kistner, Klaus-Peter : Optimierungsmethoden, Heidelberg, 2. A., 1993
Kistner, Klaus-Peter/Steven, Marion : Produktionsplanung, Heidelberg, 3. A., 2001
Kuhn, Harold W./Tucker, Albert W. : Non-Linear Programming, in: Proceedings of the Second Berkeley Symposium of Mathematical Statistics and Probability, hrsg. v. Neyman, Jerzy, Berkeley, Cal 1950, S. 481 – 492
Künzi, Hans Paul/Krelle, Wilhelm/v. Randow, Rabe : Nichtlineare Programmierung, Berlin et al., 2. A., 1979
Law, Averill M./Kelton, David W. : Simulation Modeling and Analysis, New York et al., 2. A., 1991
Manne, Alan S. : On the Job-Shop Scheduling Problem, in: Operations Research, Jg. 8, 1960, S. 219 – 223
Markowitz, Harry M. : Portfolio Selection, New York 1969
Neumann, Klaus/Morlock, Martin : Operations Research, München 1993
Schneeweiß, Christoph : Dynamisches Programmieren, Würzburg et al. 1974
Wagner, Harvey M./Whitin, Thomson M. : Dynamic Model of the Economic Lot Size Model, in: Management Science, 1958/59, Bd. 5, S. 89 – 96
Weingartner, Martin H. : Mathematical Programming and the Analysis of Capital Budgeting, Englewood Cliffs 1963
|